Siguiente: El objetivo de la Subir: Introducción Anterior: Definición cuantitativa de calor
Conviene detenernos un momento en la notación de la ecuación anterior. Como
los
![]() y
y
![]() dependen del camino recorrido, son diferenciales
imperfectos, y por ello se han denotado con una barra encima de la ``d''. En
el caso de la energía interna, en cambio,
dependen del camino recorrido, son diferenciales
imperfectos, y por ello se han denotado con una barra encima de la ``d''. En
el caso de la energía interna, en cambio, ![]() es un diferencial
exacto, pues sus variaciones son independientes de los caminos
recorridos.
es un diferencial
exacto, pues sus variaciones son independientes de los caminos
recorridos.
En cursos anteriores habíamos considerado funciones ![]() dependientes de
las variables independientes
dependientes de
las variables independientes ![]() e
e ![]() . Si
. Si ![]() es diferenciable podemos
escribir su diferencial
es diferenciable podemos
escribir su diferencial
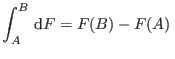 (independientemente de
la trayectoria elegida)
(independientemente de
la trayectoria elegida)
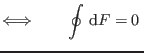 ;
;
Obviamente, las variables de estado que utilizamos en termodinámica poseen
diferenciales exactos. En particular, dadas tres variables de estado ![]() conectadas por la relación
conectadas por la relación
![]() , recurriremos a menudo a las
siguientes propiedades:
, recurriremos a menudo a las
siguientes propiedades:
Cuando existe una relación adicional
![]() , vale también la siguiente
identidad:
, vale también la siguiente
identidad:
Gustavo Castellano 12/06/2018