Gases ideales cuánticos (basado en el texto de Reichl)

Hemos visto ya que, al estudiar sistemas abiertos en equilibrio termodinámico mediante el ensamble gran canónico, las fluctuaciones en el número de partículas son despreciables, por lo que es equivalente el planteo de cualquier problema en el ensamble canónico o en el gran canónico. Esto nos permite abordar el estudio de los gases ideales cuánticos en el formalismo gran canónico, evitando inconvenientes algebraicos muy complicados para resolver en el ensamble canónico (o microcanónico).

Partimos entonces de la expresión para la gran partición

$$Z_{\mu}(T,V) = {\rm Tr} \left[ e^{-\beta(\hat{H} - \mu\hat{N})} \right] \;.$$

En la representación de Fock, esta traza se evalúa fácilmente, pues $\hat{H}$ y $\hat{N}$ son diagonales. Si $\epsilon_\ell\!=\!\hbar^2 k_\ell^2/(2m)$ es la energía cinética de una partícula en el estado ${p}$$_\ell\!=\!\hbar$${k}$$_\ell$, para el caso general obtenemos

$$Z_{\mu}(T,V) = \sum_{n_o=0}^\infty \cdots \sum_{n_j=0}^\infty \c... ...,n_\infty)\; e^{-\beta \sum_{\ell=0}^\infty n_\ell(\epsilon_\ell-\mu)} \;,$$

donde el factor $S(N;n_o,\dots,n_\infty)$ representa el número de configuraciones diferentes con esos números de ocupación o poblaciones y debe cumplirse $\sum_{\ell=0}^\infty n_\ell\!=\!N$. La diferencia entre los comportamientos que se describen reside en este factor estadístico $S$, que tiene en cuenta si deben satisfacerse las estadísticas de Maxwell-Boltzmann, Bose-Einstein o Fermi-Dirac.

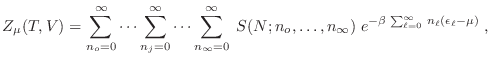
Definimos las partículas de Maxwell-Boltzmann como aquellas cuya función de onda conjunta no satisface el postulado de simetrización, sino que pueden pensarse como partículas distinguibles que obedecen la cuántica, a las que aplicamos el contaje correcto de Boltzmann introducido en §4.1.1 (ese misterioso denominador $N!$). Si bien este enfoque no representa ningún sistema físico, reviste cierto interés académico que se evidenciará pronto.

En el caso de partículas distinguibles, la expresión para el factor estadístico se obtiene de manera directa:

$$S_{\rm dist}(N;n_o,\dots,n_\infty) = \frac{N!}{n_o!\dots n_j!\dots n_\infty!} \;.$$

Con este factor la función gran partición adopta una expresión algo difícil de evaluar en virtud del numerador $N!$, por lo que en este caso generalmente se utiliza el ensamble canónico. Sin embargo, para el caso de Maxwell-Boltzmann, el contaje correcto simplifica las cuentas, resultando

$$Z_\mu^{\rm (MB)}(T,V) = \sum_{n_o=0}^\infty\cdots\sum_{n_\infty=0... ...ots n_\infty!} e^{-\beta \sum_{\ell=0}^\infty n_\ell(\epsilon_\ell-\mu)} \;.$$ (18)

En la próxima sección veremos que esta expresión puede evaluarse de manera muy directa.

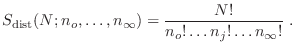
Para el caso de bosones, cualquier conjunto $\{n_j\}$ representa un único estado posible, sin restricción alguna sobre los valores de los números de ocupación, lo que implica que siempre el factor estadístico $S$ vale 1:

$$Z_\mu^{\rm (BE)}(T,V) = \sum_{n_o=0}^\infty\cdots\sum_{n_\infty=0}^\infty\; e^{-\beta \sum_{\ell=0}^\infty n_\ell(\epsilon_\ell-\mu)} \;.$$ (19)

Para temperaturas suficientemente altas, todos los números de ocupación valen a lo sumo 1, ya que todos los estados son igualmente probables, de modo que coinciden las descripciones de Maxwell-Boltzmann y la de Bose-Einstein.

Para fermiones, también cada conjunto $\{n_j\}$ representa un único estado, pero ahora deben restringirse los números de ocupación posibles a 0 ó 1:

$$Z_\mu^{\rm (FD)}(T,V) = \sum_{n_o=0}^1 \cdots \sum_{n_\infty=0}^1\; e^{-\beta \sum_{\ell=0}^\infty n_\ell(\epsilon_\ell-\mu)} \;.$$ (20)

Claramente, todas las particiones coinciden a $T$ suficientemente altas.