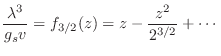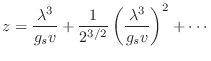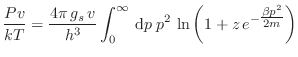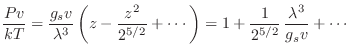En la sección 6.4 habíamos obtenido la función gran partición para
un sistema de partículas regido por la estadística de Fermi-Dirac. En la
correspondiente expresión (20), el índice 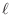 debe señalar
unívocamente el estado cuántico accesible a cada partícula: por ejemplo,
para partículas de espín 1/2, este índice debe abarcar los posibles estados
de impulso
debe señalar
unívocamente el estado cuántico accesible a cada partícula: por ejemplo,
para partículas de espín 1/2, este índice debe abarcar los posibles estados
de impulso
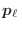 y también las proyecciones `up' (
y también las proyecciones `up' ( ) o
`down' (
) o
`down' (
 ) para el espín. Para el caso de partículas libres, los
autovalores individuales para el hamiltoniano no dependen de la orientación
del espín
) para el espín. Para el caso de partículas libres, los
autovalores individuales para el hamiltoniano no dependen de la orientación
del espín 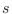 , por lo que deben repetirse
, por lo que deben repetirse
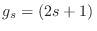 veces las sumatorias
sobre los diferentes estados de impulso. Como esta suma solo puede abarcar
dos números de ocupación posibles en cada estado (0 y 1, pues se trata de
fermiones), la gran partición puede expresarse como
veces las sumatorias
sobre los diferentes estados de impulso. Como esta suma solo puede abarcar
dos números de ocupación posibles en cada estado (0 y 1, pues se trata de
fermiones), la gran partición puede expresarse como
Podemos entonces escribir para el gran potencial
y de aquí derivamos el número medio de partículas
Como el número total de partículas se construye sumando las contribuciones
medias de todos los niveles
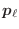 , obtenemos para el número medio de
partículas en el estado
, obtenemos para el número medio de
partículas en el estado 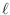
donde hemos separado la probabilidad
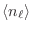 de ocupar el estado
de ocupar el estado  , debida solo al carácter estadístico de las partículas bajo estudio (en este caso fermiones). Vemos en primer lugar que siempre se cumple
, debida solo al carácter estadístico de las partículas bajo estudio (en este caso fermiones). Vemos en primer lugar que siempre se cumple
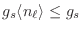 , tal
, tal
|
como exige el principio de exclusión, por lo que evidentemente no habrá
condensación en el caso de fermiones. Por otro lado, es interesante analizar
la población media del estado fundamental,
que nunca diverge, pues 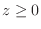 . .
Vale la pena notar que la expresión para las poblaciones medias
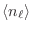 nos indica que si la temperatura alcanza el cero absoluto
( nos indica que si la temperatura alcanza el cero absoluto
(
 ), todos los niveles se despueblan excepto aquellos para los
que ), todos los niveles se despueblan excepto aquellos para los
que
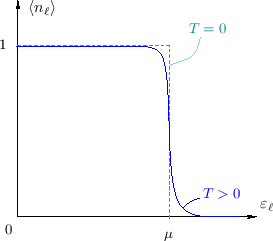
 . Cuando la temperatura es apenas superior, la distribución se aparta suavemente de la correspondiente a . Cuando la temperatura es apenas superior, la distribución se aparta suavemente de la correspondiente a
|
|
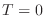 , como se
indica en la figura. La derivada de esta distribución se anula rápidamente cuando
, como se
indica en la figura. La derivada de esta distribución se anula rápidamente cuando
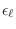 se aleja apenas de
se aleja apenas de 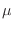 , como notaremos más adelante.
, como notaremos más adelante.
Al tomar el límite termodinámico los autovalores 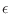 para el hamiltoniano individual de las partículas toman valores continuos, y es frecuente escribir la población estadística como
para el hamiltoniano individual de las partículas toman valores continuos, y es frecuente escribir la población estadística como
En la expresión anterior para el gran potencial, cuando tomamos el límite termodinámico podemos reemplazar la sumatoria sobre 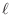 por una integral en el espacio ahora continuo de
por una integral en el espacio ahora continuo de 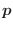 (o de
(o de 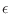 ), obteniendo
), obteniendo
donde
Para llegar a esta expresión integral es necesario realizar el cambio de
variable
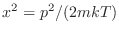 , mientras que la sumatoria se obtiene al hacer un
desarrollo en serie del integrando, resolviendo luego término a término.
, mientras que la sumatoria se obtiene al hacer un
desarrollo en serie del integrando, resolviendo luego término a término.
Es interesante señalar que podemos escribir la gran partición en términos de
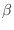 ,
, 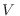 y
y 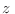 como variables independientes, en lugar de
como variables independientes, en lugar de 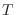 ,
, 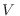 y
y 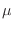 . De este modo, con un mínimo de inspiración el lector podrá mostrar
por ejemplo la siguiente relación
. De este modo, con un mínimo de inspiración el lector podrá mostrar
por ejemplo la siguiente relación
teniendo la precaución de que al derivar deben permanecer constantes 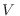 y
y 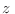 (y no
(y no 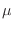 ). Se obtiene así
). Se obtiene así
mientras que para un gas de bosones con degeneración 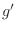 la energía
interna resulta
la energía
interna resulta
Comparando estas expresiones con
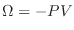 , se ve que al igual que para la estadística de Bose-Einstein se cumple
, se ve que al igual que para la estadística de Bose-Einstein se cumple
De manera semejante puede expresarse el número medio de partículas
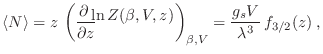 |
(22) |
donde
|
Como la función
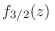 es creciente con es creciente con 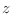 , de la expresión
anterior para , de la expresión
anterior para
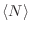 puede verse que, para una dada densidad,
cuando crece la temperatura debe decrecer puede verse que, para una dada densidad,
cuando crece la temperatura debe decrecer 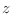 , de manera que para altas
temperaturas , de manera que para altas
temperaturas
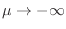 . Por otro lado, cuando la temperatura se hace
muy pequeña, . Por otro lado, cuando la temperatura se hace
muy pequeña, 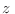 debe tender a debe tender a 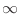 , es decir , es decir
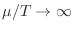 , de
donde inferimos que a bajas temperaturas , de
donde inferimos que a bajas temperaturas 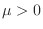 , aunque su valor puede ser
acotado, pues el denominador , aunque su valor puede ser
acotado, pues el denominador 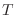 garantiza de todos modos la divergencia. garantiza de todos modos la divergencia.
Para estudiar el comportamiento de este sistema a bajas temperaturas debemos
analizar entonces el comportamiento de
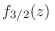 para valores de para valores de 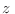 grandes. Seguiremos para ello el método de Sommerfeld, notando que estamos interesados en propiedades termodinámicas como la energía interna del sistema grandes. Seguiremos para ello el método de Sommerfeld, notando que estamos interesados en propiedades termodinámicas como la energía interna del sistema
|
|
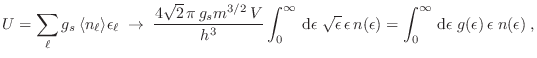 |
(23) |
o el número medio total de partículas
Al cambiar de variables, la densidad de estados
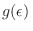 representa la fracción de estados individuales diferentes que comparten ese autovalor de energía
representa la fracción de estados individuales diferentes que comparten ese autovalor de energía 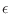 . En general entonces, tenemos integrales de la forma
. En general entonces, tenemos integrales de la forma
El desarrollo de Sommerfeld consiste en separar esta integral en dos partes
donde 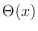 es la función escalón de Heaviside. De este modo, retenemos en el primer término del miembro de la derecha el comportamiento que sobrevivirá para el límite
es la función escalón de Heaviside. De este modo, retenemos en el primer término del miembro de la derecha el comportamiento que sobrevivirá para el límite 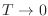 . Puede extenderse la última integral hasta
. Puede extenderse la última integral hasta 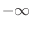 definiendo
definiendo
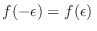 para
para
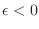 , teniendo en cuenta que
, teniendo en cuenta que
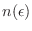 solo difiere apreciablemente de
solo difiere apreciablemente de
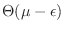 en un entorno cercano de
en un entorno cercano de
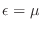 , pues para
, pues para
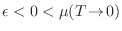 ,
,
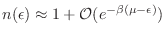
Como ejercicio sencillo, se recomienda demostrar que la función
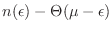 es impar alrededor de
es impar alrededor de
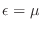 .
Podemos tomar entonces la expansión en serie de Taylor de
.
Podemos tomar entonces la expansión en serie de Taylor de
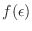 alrededor de
alrededor de 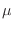 y realizar el cambio de variable
y realizar el cambio de variable
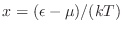 ,
notando que las potencias pares de
,
notando que las potencias pares de 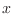 no contribuirán a la integral
no contribuirán a la integral
El producto del factor entre corchetes y las potencias impares de 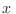 es una
función par, y dado que
es una
función par, y dado que
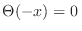 para
para 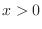 ,
,
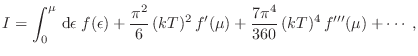 |
(24) |
donde hemos utilizado la función 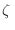 de Riemann, relacionada con la
función
de Riemann, relacionada con la
función 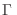 mediante la identidad
mediante la identidad
en particular,
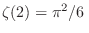 y
y
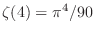 . La expansión de
Sommerfeld (24) permite reescribir el número medio de partículas
. La expansión de
Sommerfeld (24) permite reescribir el número medio de partículas
sustituyendo la integral en 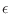 , de modo que puede despejarse el
comportamiento de
, de modo que puede despejarse el
comportamiento de
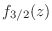 para valores grandes de
para valores grandes de 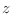 :
:
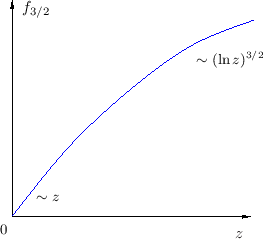
![$\displaystyle f_{3/2}(z) = \frac{4}{3\sqrt\pi} (\ln z)^{3/2} \left[ 1 +
\frac{\pi^2}8 (\ln z)^{-2} + \cdots + {\cal O}\!\left((\ln z)^{-4}\right) \right]\;.$](img1011.png) |
(25) |
Entonces, para el caso de bajas temperaturas o altas densidades, es decir
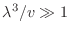 , la ecuación (22) puede aproximarse como
, la ecuación (22) puede aproximarse como
En particular, se define como energía de Fermi
Completamos ahora el comentario de más arriba diciendo que a 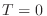 si
si
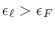 ,
, 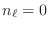 , y si
, y si
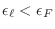 ,
,
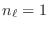 .
.
Se define también el impulso de Fermi 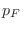 escribiendo la relación
clásica
escribiendo la relación
clásica
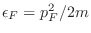 . Más frecuentemente se utiliza la temperatura de Fermi
. Más frecuentemente se utiliza la temperatura de Fermi
 , de manera que si
, de manera que si
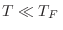 se dice que el gas está “degenerado”, porque todas las partículas
tienden a ocupar los estados de menor energía, según lo permitido por la
degeneración
se dice que el gas está “degenerado”, porque todas las partículas
tienden a ocupar los estados de menor energía, según lo permitido por la
degeneración 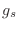 .
.
La expansión (25) puede “invertirse”, resultando en esta región
Podemos obtener una expresión para la energía interna de este sistema
desarrolando análogamente la expansión (23), siguiendo también el método de
Sommerfeld. Se deja como ejercicio verificar
El primer término corresponde a la energía del estado fundamental, y puede
verificarse fácilmente que
Con estos elementos puede calcularse el calor específico
Aquí se pone en evidencia que se cumple la tercera ley de la termodinámica,
ya que este calor específico tiende a cero en el límite de bajas temperaturas.
A partir de la igualdad 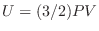 puede escribirse
puede escribirse
Podemos ver que a 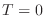 ,
, 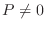 , como consecuencia del principio de
exclusión, pues no todas las partículas pueden tener el mínimo valor de
impulso.
, como consecuencia del principio de
exclusión, pues no todas las partículas pueden tener el mínimo valor de
impulso.
Analicemos a continuación el régimen de temperaturas altas o bajas
densidades, es decir,
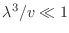 , donde esperamos que los efectos
cuánticos se “disimulen”. Recordando que en este caso
, donde esperamos que los efectos
cuánticos se “disimulen”. Recordando que en este caso 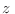 toma valores
muy próximos a 0, aproximamos
toma valores
muy próximos a 0, aproximamos
Como antes, “invirtiendo” esta serie tenemos
En los casos en que
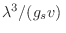 es extremadamente pequeño, podemos
quedarnos solo con el primer término, coincidiendo nuestro resultado con el
correspondiente al gas de Maxwell-Boltzmann. Por otro lado, puede
verificarse que las poblaciones de los distintos niveles también coinciden
con el caso de Maxwell-Boltzmann. Finalmente, la ecuación de estado
es extremadamente pequeño, podemos
quedarnos solo con el primer término, coincidiendo nuestro resultado con el
correspondiente al gas de Maxwell-Boltzmann. Por otro lado, puede
verificarse que las poblaciones de los distintos niveles también coinciden
con el caso de Maxwell-Boltzmann. Finalmente, la ecuación de estado
puede aproximarse como
Nuevamente, el resultado coincide con el de Maxwell-Boltzmann en la
situación límite.
Subsecciones
Gustavo Castellano 19/11/2021
![]() debe señalar
unívocamente el estado cuántico accesible a cada partícula: por ejemplo,
para partículas de espín 1/2, este índice debe abarcar los posibles estados
de impulso
debe señalar
unívocamente el estado cuántico accesible a cada partícula: por ejemplo,
para partículas de espín 1/2, este índice debe abarcar los posibles estados
de impulso
![]() y también las proyecciones `up' (
y también las proyecciones `up' (![]() ) o
`down' (
) o
`down' (
![]() ) para el espín. Para el caso de partículas libres, los
autovalores individuales para el hamiltoniano no dependen de la orientación
del espín
) para el espín. Para el caso de partículas libres, los
autovalores individuales para el hamiltoniano no dependen de la orientación
del espín ![]() , por lo que deben repetirse
, por lo que deben repetirse
![]() veces las sumatorias
sobre los diferentes estados de impulso. Como esta suma solo puede abarcar
dos números de ocupación posibles en cada estado (0 y 1, pues se trata de
fermiones), la gran partición puede expresarse como
veces las sumatorias
sobre los diferentes estados de impulso. Como esta suma solo puede abarcar
dos números de ocupación posibles en cada estado (0 y 1, pues se trata de
fermiones), la gran partición puede expresarse como
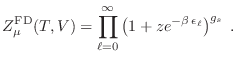
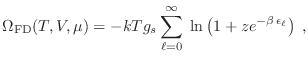
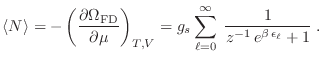
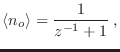
![]() , como se
indica en la figura. La derivada de esta distribución se anula rápidamente cuando
, como se
indica en la figura. La derivada de esta distribución se anula rápidamente cuando
![]() se aleja apenas de
se aleja apenas de ![]() , como notaremos más adelante.
, como notaremos más adelante.
![]() para el hamiltoniano individual de las partículas toman valores continuos, y es frecuente escribir la población estadística como
para el hamiltoniano individual de las partículas toman valores continuos, y es frecuente escribir la población estadística como
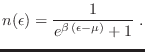
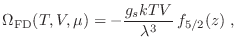
![$\displaystyle f_{5/2}(z) \equiv \frac{4}{\sqrt\pi} \int_0^\infty {\rm d}x\; ...
...um_{j=1}^\infty \frac{(-1)^{j+1} z^j}{j^{5/2}}\quad \mbox{si $z<1$}\right]\;.
$](img965.png)
![]() ,
, ![]() y
y ![]() como variables independientes, en lugar de
como variables independientes, en lugar de ![]() ,
, ![]() y
y ![]() . De este modo, con un mínimo de inspiración el lector podrá mostrar
por ejemplo la siguiente relación
. De este modo, con un mínimo de inspiración el lector podrá mostrar
por ejemplo la siguiente relación
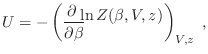
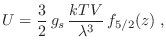
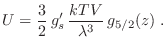
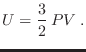
![$\displaystyle f_{3/2}(z) \equiv \frac{4}{\sqrt\pi} \int_0^\infty {\rm d}x\; ...
...um_{j=1}^\infty \frac{(-1)^{j+1} z^j}{j^{3/2}}\quad \mbox{si $z<1$}\right]\;.
$](img974.png)
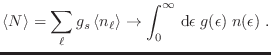

![$\displaystyle I = \int_0^\mu {\rm d}\epsilon\; f(\epsilon) + \int_0^\infty ...
...\epsilon)\; \left[ \rule{0em}{1em}n(\epsilon)-\Theta(\mu-\epsilon) \right] \;,
$](img985.png)
![$\displaystyle I \approx \int_0^\mu {\rm d}\epsilon\; f(\epsilon) +
\int_{-\i...
...epsilon)\;
\left[ \rule{0em}{1em}n(\epsilon)-\Theta(\mu-\epsilon) \right] \;.
$](img995.png)
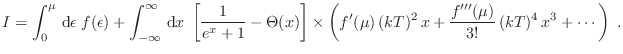
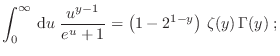
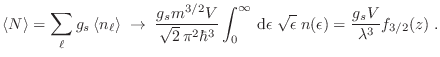
![$\displaystyle \frac1v = \frac{4}{3\sqrt\pi} (\ln z)^{3/2} \frac{g_s}{\lambda^3} \left[ 1 +
\frac{\pi^2}8 (\ln z)^{-2} + \cdots \right]
$](img1013.png)
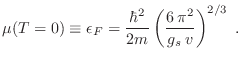
![]() escribiendo la relación
clásica
escribiendo la relación
clásica
![]() . Más frecuentemente se utiliza la temperatura de Fermi
. Más frecuentemente se utiliza la temperatura de Fermi
![]() , de manera que si
, de manera que si
![]() se dice que el gas está “degenerado”, porque todas las partículas
tienden a ocupar los estados de menor energía, según lo permitido por la
degeneración
se dice que el gas está “degenerado”, porque todas las partículas
tienden a ocupar los estados de menor energía, según lo permitido por la
degeneración ![]() .
.
![$\displaystyle \mu \; (= kT \ln z) = \epsilon_F \left[ 1 -
\frac{\pi^2}{12}\left(\frac{kT}{\epsilon_F}\right)^2 +\cdots \right] \;.
$](img1025.png)
![$\displaystyle U = \frac35 \langle N \rangle \epsilon_F \left[ 1 +
\frac5{12} \pi^2\left(\frac{kT}{\epsilon_F}\right)^2 + \cdots \right] \;.
$](img1026.png)
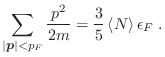
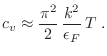
![]() puede escribirse
puede escribirse
![$\displaystyle P \approx \frac25 \frac{\epsilon_F}v \left[ 1 +
\frac{5\pi^2}{12} \left(\frac{kT}{\epsilon_F}\right)^2 + \cdots \right]\;.
$](img1030.png)
![]() , donde esperamos que los efectos
cuánticos se “disimulen”. Recordando que en este caso
, donde esperamos que los efectos
cuánticos se “disimulen”. Recordando que en este caso ![]() toma valores
muy próximos a 0, aproximamos
toma valores
muy próximos a 0, aproximamos