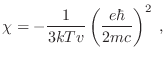En un campo magnético externo asociado a un potencial vector  , el
hamiltoniano no relativista correspondiente a un electrón “libre” es
, el
hamiltoniano no relativista correspondiente a un electrón “libre” es
La ecuación de Schrödinger independiente de  es invariante ante
transformaciones de gauge
es invariante ante
transformaciones de gauge
donde
 es cualquier función continua. Si
es cualquier función continua. Si
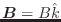 ,
podemos elegir
,
podemos elegir
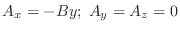 ,
con lo cual obtenemos
,
con lo cual obtenemos
Proponiendo
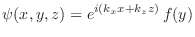 , donde
, donde
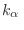 es el autovalor respectivo para
es el autovalor respectivo para 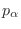 , la
ecuación de Schrödinger estacionaria correspondiente al autovalor de energía
, la
ecuación de Schrödinger estacionaria correspondiente al autovalor de energía
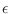 implica
implica
donde
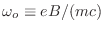 es la frecuencia ciclotrónica
correspondiente a las órbitas circulares clásicas de una masa
es la frecuencia ciclotrónica
correspondiente a las órbitas circulares clásicas de una masa 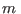 con
carga
con
carga 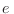 bajo un campo
bajo un campo 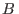 uniforme,
uniforme,
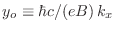 y
y
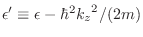 . La anterior ecuación para
. La anterior ecuación para
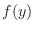 no es otra que la entrañable ecuación de un oscilador armónico, de
manera que los autovalores de
no es otra que la entrañable ecuación de un oscilador armónico, de
manera que los autovalores de 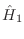 son los niveles de Landau
son los niveles de Landau
donde
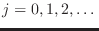 y
y
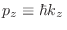 son los autovalores de
partícula libre según la dirección
son los autovalores de
partícula libre según la dirección 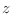 .
.
Notemos que los niveles de Landau son independientes de 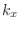 , lo que
significa que habrá una degeneración para ellos igual al número de valores
de
, lo que
significa que habrá una degeneración para ellos igual al número de valores
de 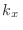 permitidos en cada caso, de manera que el valor de
permitidos en cada caso, de manera que el valor de 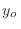 no
escape del volumen que contiene a los electrones. Suponiendo que se trata de
un material cúbico de lado
no
escape del volumen que contiene a los electrones. Suponiendo que se trata de
un material cúbico de lado 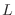 , e imponiendo condiciones periódicas a
, e imponiendo condiciones periódicas a
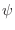 , los valores permitidos para
, los valores permitidos para 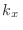 resultan
resultan
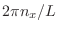 , donde
, donde
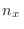 es un número natural. En ese caso,
es un número natural. En ese caso,
de modo que la condición
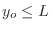 implica
implica
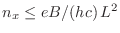 , o
equivalentemente, la correspondiente degeneración será
, o
equivalentemente, la correspondiente degeneración será
Vemos entonces que cuando aparece un campo externo 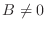 , las energías
asociadas con el movimiento en el plano
, las energías
asociadas con el movimiento en el plano 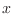 -
-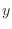 dejan de ser continuas para
tomar los valores discretos que hemos encontrado aquí.
dejan de ser continuas para
tomar los valores discretos que hemos encontrado aquí.
Para obtener la función gran partición debemos desarrollar adecuadamente la
expresión
donde aquí los estados posibles son señalados por los números cuánticos
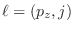 o
o
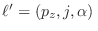 en nuestra notación previa,
representando los valores posibles para
en nuestra notación previa,
representando los valores posibles para 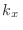 con el índice
con el índice
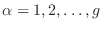 . Tenemos entonces
. Tenemos entonces
Como
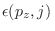 no depende de
no depende de 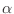 , sumar sobre este índice
simplemente implica repetir
, sumar sobre este índice
simplemente implica repetir 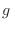 veces el resto de la expresión. En el
límite termodinámico, los autovalores de
veces el resto de la expresión. En el
límite termodinámico, los autovalores de 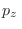 pasan a ser continuos, de
modo que la suma se transforma en integral mediante el procedimiento
habitual
pasan a ser continuos, de
modo que la suma se transforma en integral mediante el procedimiento
habitual
donde hemos reducido el intervalo de integración sobre 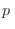 a partir de la
paridad del integrando. El número medio de partículas resulta entonces
a partir de la
paridad del integrando. El número medio de partículas resulta entonces
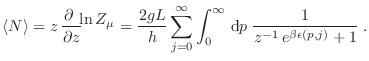 |
(26) |
Para temperaturas altas, 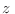 se aproxima a cero, de modo que el valor de
se aproxima a cero, de modo que el valor de
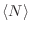 no diverja. Utilizando entonces el hecho de que
no diverja. Utilizando entonces el hecho de que 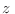 es pequeño, podemos aproximar
es pequeño, podemos aproximar
Ahora la integración y la suma se resuelven independientemente, y definiendo
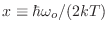 obtenemos
obtenemos
Como 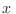 es pequeño para temperaturas altas, podemos desarrollar en serie
de Taylor, teniendo el cuidado de agrupar pertinentemente los términos del
mismo orden. Así obtenemos
es pequeño para temperaturas altas, podemos desarrollar en serie
de Taylor, teniendo el cuidado de agrupar pertinentemente los términos del
mismo orden. Así obtenemos
de donde puede obtenerse una estimación para la susceptibilidad
La primera gran sorpresa es que este tratamiento cuántico nos ha permitido
obtener una respuesta magnética no nula. Pero además, el hecho de que
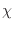 sea negativo implica que estamos dando cuenta de un comportamiento
diamagnético del material en cuestión, lo que nos mantendrá por un
tiempo en un éxtasis irrefrenable.
sea negativo implica que estamos dando cuenta de un comportamiento
diamagnético del material en cuestión, lo que nos mantendrá por un
tiempo en un éxtasis irrefrenable.
Para 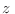 pequeños la ecuación (26) provee una expresión que
coincide con
pequeños la ecuación (26) provee una expresión que
coincide con 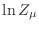 , de manera que podemos aproximar
, de manera que podemos aproximar
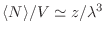 . Reemplazando
. Reemplazando 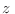 en la expresión para
en la expresión para
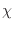 obtenemos
obtenemos
que en particular satisface la ley de Curie (
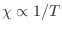 ).
).
Gustavo Castellano 19/11/2021
![]() , el
hamiltoniano no relativista correspondiente a un electrón “libre” es
, el
hamiltoniano no relativista correspondiente a un electrón “libre” es
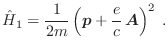
![$\displaystyle \hat H_1 = \frac 1{2m} \left[ \left(p_x-\frac{eB}{c}\,y\right)^2 +
{p_y}^2 + {p_z}^2 \right] \;.
$](img1057.png)
![$\displaystyle \left[\frac1{2m} {p_y}^2 + \frac12 m {\omega_o}^2 (y-y_o)^2\right] f(y)
= \epsilon'\; f(y) \;,
$](img1061.png)
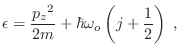
![]() , lo que
significa que habrá una degeneración para ellos igual al número de valores
de
, lo que
significa que habrá una degeneración para ellos igual al número de valores
de ![]() permitidos en cada caso, de manera que el valor de
permitidos en cada caso, de manera que el valor de ![]() no
escape del volumen que contiene a los electrones. Suponiendo que se trata de
un material cúbico de lado
no
escape del volumen que contiene a los electrones. Suponiendo que se trata de
un material cúbico de lado ![]() , e imponiendo condiciones periódicas a
, e imponiendo condiciones periódicas a
![]() , los valores permitidos para
, los valores permitidos para ![]() resultan
resultan
![]() , donde
, donde
![]() es un número natural. En ese caso,
es un número natural. En ese caso,
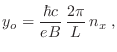
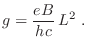
![]() , las energías
asociadas con el movimiento en el plano
, las energías
asociadas con el movimiento en el plano ![]() -
-![]() dejan de ser continuas para
tomar los valores discretos que hemos encontrado aquí.
dejan de ser continuas para
tomar los valores discretos que hemos encontrado aquí.
![$\displaystyle \ln Z_\mu = \sum_{\alpha=1}^g \sum_{j=0}^\infty \sum_{p_z}\;
\ln \left[ 1 + z e^{-\beta \epsilon(p_z,j)} \right] \;.
$](img1088.png)
![$\displaystyle \ln Z_\mu = \frac{2gL}h \sum_{j=0}^\infty \int_0^\infty {\rm d}p\;
\ln \left[ 1 + z e^{-\beta \epsilon(p,j)} \right] \;,
$](img1092.png)
![]() se aproxima a cero, de modo que el valor de
se aproxima a cero, de modo que el valor de
![]() no diverja. Utilizando entonces el hecho de que
no diverja. Utilizando entonces el hecho de que ![]() es pequeño, podemos aproximar
es pequeño, podemos aproximar
![$\displaystyle \ln Z_\mu \simeq \frac{2gzL}h \sum_{j=0}^\infty \int_0^\infty {...
...e\frac{p≤}{2m}} +
\hbar\omega_o\left(j+{\textstyle\frac12}\right)\right]} \;.
$](img1094.png)
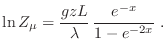
![$\displaystyle \ln Z_\mu \simeq \frac{gzL}{\lambda} \frac1{2x}\left(1-\frac{x^2...
...da≥} \left[ 1 -
\frac1{24}\left(\frac{\hbar\omega_o}{kT}\right)^2 \right] \;,
$](img1097.png)
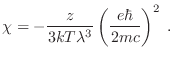
![]() pequeños la ecuación (26) provee una expresión que
coincide con
pequeños la ecuación (26) provee una expresión que
coincide con ![]() , de manera que podemos aproximar
, de manera que podemos aproximar
![]() . Reemplazando
. Reemplazando ![]() en la expresión para
en la expresión para
![]() obtenemos
obtenemos