Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Mecánica
Guía N 0: Antes del Comienzo
0: Antes del Comienzo
Problema 1: Considere una partícula cuya trayectoria está descripta
por el vector 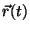 .
.
a) Calcular el elemento diferencial de arco de la
trayectoria (
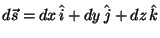 ) y su módulo cuadrado (
) y su módulo cuadrado (
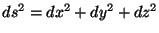 )
en coordenadas cilíndricas y esféricas.
)
en coordenadas cilíndricas y esféricas.
b) Expresar las componentes cartesianas del
vector 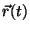 en coordenadas cilíndricas y esféricas.
en coordenadas cilíndricas y esféricas.
c) Expresar al vector 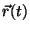 en la base de un
sistema de coordenadas cartesianas, cilíndricas y esféricas.
en la base de un
sistema de coordenadas cartesianas, cilíndricas y esféricas.
d) Expresar al vector 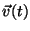 en la base de un
sistema de coordenadas cartesianas, cilíndricas y esféricas.
en la base de un
sistema de coordenadas cartesianas, cilíndricas y esféricas.
e) Expresar el módulo cuadrado del vector velocidad
en coordenadas cartesianas, cilíndricas y esféricas.
Problema 2: Sea 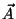 un vector constante, y sea
un vector constante, y sea
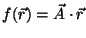 . Calcular el gradiente de
. Calcular el gradiente de 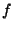 ,
esto es
,
esto es
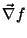 , coordenadas cartesianas, cilíndricas
y esféricas.
, coordenadas cartesianas, cilíndricas
y esféricas.
Problema 3: Sean 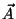 y
y 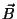 dos vectores.
Calcular
dos vectores.
Calcular
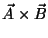 en la base de un sistema de
coordenadas cartesianas, cilíndricas y esféricas.
en la base de un sistema de
coordenadas cartesianas, cilíndricas y esféricas.
Problema 4: Considere una partícula de masa 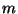 , que se mueve bajo la
acción del siguiente potencial:
, que se mueve bajo la
acción del siguiente potencial:
donde 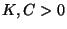 y
y 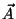 es un vector constante.
es un vector constante.
a) Calcule el vector aceleración de la
partícula.
Considere un sistema de coordenadas cuyo eje 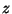 es
paralelo al vector
es
paralelo al vector 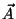 :
:
b) Calcule las componentes cartesianas de la fuerza
que actúa sobre la partícula.
c) Calcule las componentes en la base de coordenadas
esféricas, de la fuerza que actúa sobre la partícula.
d) Calcule las componentes en la base de coordenadas
cilíndricas, de la fuerza que actúa sobre la partícula.
Fa.M.A.F ©2000
Pedro Pury
2000-12-18