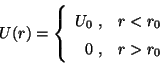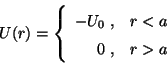Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Mecánica
Guía N 4: Potencial Central y Dispersión
4: Potencial Central y Dispersión
Problema 1: Considere el péndulo esférico: Una partícula
de masa 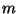 restringida a moverse en la superficie de una esfera de
radio
restringida a moverse en la superficie de una esfera de
radio 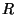 , bajo la acción de la gravedad
, bajo la acción de la gravedad
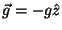 .
.
a) Escribir el Lagrangeano del sistema en coordenadas
esféricas
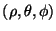 y determinar las coordenadas
cíclicas y cantidades conservadas.
y determinar las coordenadas
cíclicas y cantidades conservadas.
b) Definir una energía potencial
efectiva
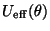 e integrar las ecuaciones de
Euler-Lagrange. Determine (al menos cualitativamente) las regiones
permitidas para el movimiento de la partícula.
e integrar las ecuaciones de
Euler-Lagrange. Determine (al menos cualitativamente) las regiones
permitidas para el movimiento de la partícula.
Problema 2: Determinar las posibles trayectorias de una partícula
en el siguiente potencial central:
Problema 3: Para una partícula se mueve en un potencial central
Kepleriano
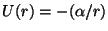 , se define el vector de
Lenz
, se define el vector de
Lenz 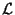 según:
según:
a) Demuestre que 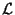 se conserva para una
adecuada elección de
se conserva para una
adecuada elección de 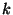 .
>En qué dirección apunta
.
>En qué dirección apunta 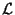 ?
?
b) Utilice la integral de movimiento 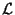 para
calcular las trayectorias del problema de Kepler.
para
calcular las trayectorias del problema de Kepler.
Problema 4: Caída al centro en un potencial central:
a) Integre las ecuaciones de movimiento para una
partícula en el campo central
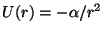 (
(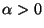 ).
Determine en qué casos la partícula cae al centro de
potencial, y cuánto tarda.
).
Determine en qué casos la partícula cae al centro de
potencial, y cuánto tarda.
b) Considere ahora el movimiento en un campo central
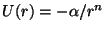 (
(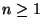 ,
, 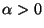 ). Determine si es finito o
no el número de vueltas realizadas por la partícula alrededor
del centro. Determine cuanto tarda la partícula en llegar al
centro de potencial. Resuelva la ecuación de movimiento en la
aproximación de
). Determine si es finito o
no el número de vueltas realizadas por la partícula alrededor
del centro. Determine cuanto tarda la partícula en llegar al
centro de potencial. Resuelva la ecuación de movimiento en la
aproximación de 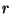 pequeño.
pequeño.
Problema 5: Determine qué potencial central admite como solución
órbitas circulares que pasan por el centro de potencial.
Solución:
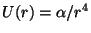 . Demostrarla!
. Demostrarla!
Problema 6: Cuando se añade al potencial central
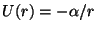 (
(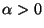 ) una pequeña corrección
) una pequeña corrección 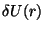 , la trayectoria
para un movimiento finito deja de ser cerrada, y con cada revolución
el perihelio de la órbita se desplaza un pequeño ángulo
, la trayectoria
para un movimiento finito deja de ser cerrada, y con cada revolución
el perihelio de la órbita se desplaza un pequeño ángulo
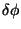 . Determine
. Determine 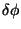 para:
a)
para:
a)
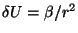 ;
b)
;
b)
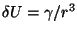 .
.
Problema 7: Un oscilador armónico tridimensional consiste en una
partícula de masa 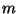 que se mueve en el potencial
que se mueve en el potencial
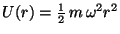 .
.
a) Integre las ecuaciones de movimiento, y muestre
que las órbitas son elipses centradas en el origen.
b) Obtenga la velocidad angular de precesión cuando
se agrega una pequeña perturbación
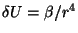 .
.
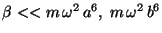 , donde
, donde 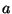 y
y 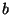 son los parámetros de la trayectoria no perturbada:
son los parámetros de la trayectoria no perturbada:
Problema 8: Una partícula está atraída hacia un punto
fijo por una fuerza 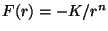 ,
, 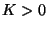 . Utilice un análisis
perturbativo para demostrar que cuando
. Utilice un análisis
perturbativo para demostrar que cuando 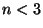 es posible encontrar
órbitas circulares estables.
es posible encontrar
órbitas circulares estables.
Problema 9: Generalice el teorema del virial para sistemas que incluyan
fuerzas de rozamiento proporcionales a la velocidad.
Problema 10: Determine la sección eficaz para captura de meteoritos
por la Tierra en función de 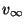 y el parámetro de
impacto
y el parámetro de
impacto 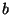 . Suponga como condición de captura que la distancia
al centro de la Tierra en el perigeo de la órbita sea menor que
el radio terrestre.
. Suponga como condición de captura que la distancia
al centro de la Tierra en el perigeo de la órbita sea menor que
el radio terrestre.
Problema 11: Determine la sección eficaz diferencial y total de
dispersión respecto del centro de masa en cada uno de los
siguientes casos:
a) Pozo de potencial esférico de radio 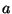 y
profundidad
y
profundidad 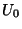 :
:
b)
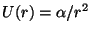 (
(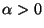 ).
).
Problema 12: Considere la colisión elástica de dos partículas de
masas 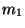 y
y 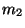 . Determine el ángulo de desviación
. Determine el ángulo de desviación 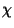 respecto del centro de masa en función del ángulo
respecto del centro de masa en función del ángulo 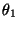 y en función del ángulo
y en función del ángulo 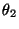 , correspondientes a las
desviaciones de las partículas respecto del sistema laboratorio.
, correspondientes a las
desviaciones de las partículas respecto del sistema laboratorio.
Problema 13: Calcular la sección eficaz total de captura para un
potencial central de la forma
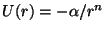 (
(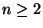 y
y
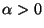 ).
La captura es la situación en la cual la partícula cae
al centro del potencial.
).
La captura es la situación en la cual la partícula cae
al centro del potencial.
Problema 14: Calcular la sección eficaz total para un haz de
partículas incidente, paralelo al eje 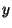 , sobre un cubo
rígido de lado
, sobre un cubo
rígido de lado 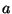 , cuyas caras son paralelas a los planos
definidos por los ejes Cartesianos.
, cuyas caras son paralelas a los planos
definidos por los ejes Cartesianos.
Fa.M.A.F ©2000
Pedro Pury
2000-12-18