Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Mecánica
Guía N 5: Cuerpo Rígido
5: Cuerpo Rígido
Problema 1: Determine los momentos principales de inercia para los
siguientes cuerpos rígidos:
a) Molécula de cuatro átomos que forman un
tetraedro de base equilátera. Los tres átomos de la base
son de masa 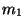 y forman un triángulo equilátero de lado
y forman un triángulo equilátero de lado 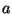 ;
mientras que el cuarto átomo, de masa
;
mientras que el cuarto átomo, de masa 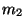 , dista del centro de
la base a una distancia
, dista del centro de
la base a una distancia 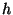 . Considere tambien el caso del tetraedro
regular con todos los átomos de igual masa y caras equiláteras.
. Considere tambien el caso del tetraedro
regular con todos los átomos de igual masa y caras equiláteras.
b) Cilindro circular homogéneo de radio 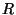 y
altura
y
altura 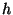 .
.
c) Cono circular homogéneo de altura 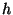 y radio de
la base
y radio de
la base 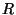 .
.
d) Elipsoide homogéneo de semiejes 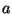 ,
, 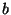 y
y 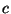 .
.
e) Esfera homogénea de radio 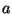 , en cuyo interior
se halla una cavidad esférica de radio
, en cuyo interior
se halla una cavidad esférica de radio 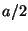 , cuyo centro está
desplazado respecto del primero una distancia
, cuyo centro está
desplazado respecto del primero una distancia 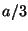 .
.
Problema 2: Mostrar que si se desplaza el origen del sistema de
coordenadas según un vector 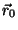 , el tensor de inercia
respecto del nuevo origen tendrá el mismo sistema de ejes
principales (salvo traslaciones), si el primitivo origen del sistema
de coordenadas coincide con el centro de masa y si
, el tensor de inercia
respecto del nuevo origen tendrá el mismo sistema de ejes
principales (salvo traslaciones), si el primitivo origen del sistema
de coordenadas coincide con el centro de masa y si 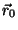 tiene
la dirección de uno de los ejes principales de inercia.
tiene
la dirección de uno de los ejes principales de inercia.
Problema 3: Usando las correspondientes condiciones de vínculo,
calcular la energía cinética de los siguientes cuerpos
rígidos:
a) Un cilindro inhomogéneo de radio 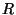 , que
rueda sobre un plano. La masa se encuentra distribuída de forma
tal que un eje principal de inercia resulta paralelo al eje del
cilindro y el centro de masa se encuentra desplazado una distancia
, que
rueda sobre un plano. La masa se encuentra distribuída de forma
tal que un eje principal de inercia resulta paralelo al eje del
cilindro y el centro de masa se encuentra desplazado una distancia
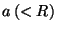 del eje geométrico. El correspondiente momento de
inercia asociado a dicho eje principal es
del eje geométrico. El correspondiente momento de
inercia asociado a dicho eje principal es 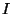 .
.
b) Un cilindro homogéneo de radio 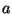 que rueda
dentro de una superficie cilíndrica de radio
que rueda
dentro de una superficie cilíndrica de radio 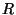 .
.
c) Un cono homogéneo que rueda sobre un plano.
d) Un cono homogéneo cuya base rueda sobre un plano
y cuyo vértice está fijo a una altura sobre el plano igual al
radio de la base, de modo que el eje del cono queda paralelo al
plano.
e) Un elipsoide homogéneo que rota alrededor de uno
de sus ejes principales (respecto del cual es simétrico), el cual
a su vez gira alrededor de un eje vertical con el cual forma un
ángulo 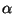 constante.
constante.
Problema 4: Considerar un trompo simétrico en el campo gravitatorio,
cuyo punto inferior está fijo.
a) Construir el Lagrangeano. Determinar las cantidades
conservadas, y a partir de estas estudiar el movimiento del cuerpo.
b) Determinar la condición de estabilidad para la
rotación del trompo alrededor de un eje vertical.
c) Determinar el movimiento del trompo para el caso
en que la energía cinética de rotación alrededor de su eje
de simetría sea grande comparada con su energía en el campo
gravitacional (trompo rápido).
Problema 5: Considere un disco plano de radio 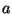 y espesor
y espesor 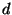 , delgado
(
, delgado
(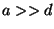 ) y simétrico respecto de su eje, que puede rotar y
deslizarse libremente apoyado sobre una superficie plana horizontal
sin rozamiento. Para describir su movimiento considere un
sistema de coordenadas cartesianas cuyo eje
) y simétrico respecto de su eje, que puede rotar y
deslizarse libremente apoyado sobre una superficie plana horizontal
sin rozamiento. Para describir su movimiento considere un
sistema de coordenadas cartesianas cuyo eje 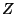 es perpendicular al
plano y los ángulos de Euler
es perpendicular al
plano y los ángulos de Euler
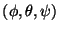 de forma tal
que
de forma tal
que 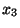 está en la dirección del eje de simtría del disco
y la intersección del plano del disco con el plano
está en la dirección del eje de simtría del disco
y la intersección del plano del disco con el plano 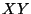 (línea
(línea
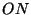 ) forma un ángulo
) forma un ángulo 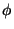 con el eje
con el eje 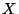 .
.
a) ¿Cuántos grados de libertad tiene el sistema?
b) Escribir la función de Lagrange.
c) Calcular las cantidades conservadas.
d) Determine bajo qué condiciones el disco rota
manteniendo el ángulo de inclinación 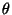 constante. Asumir
que la proyección de la velocidad angular sobre su eje es grande
comparada con toda otra proyección.
constante. Asumir
que la proyección de la velocidad angular sobre su eje es grande
comparada con toda otra proyección.
e) Determine bajo qué condiciones la rotación
del disco manteniendo su eje en posición horizontal (es decir
con
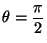 ) es estable.
) es estable.
Problema 6: Determinar las ecuaciones y estudiar el movimiento de:
a) Una esfera homogénea que rueda sin deslizar
sobre un plano inclinado bajo la acción de la gravedad.
b) Un cono que rueda sin deslizar sobre una
superficie plana.
Problema 7: Para los sólidos no simétricos no es posible resolver
analíticamente las ecuaciones de Euler en términos de
funciones elementales. Demuestre que, sin embargo, puede utilizarse
la conservación de la energía y del momento angular para
obtener expresiones (en términos de integrales elípticas) para
las componentes de 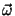 en un sistema fijo al cuerpo.
en un sistema fijo al cuerpo.
Problema 8: Un objeto es disparado verticalmente hacia arriba desde la
superficie de la tierra con velocidad inicial 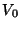 . El lugar del
disparo se encuentra en colatitud
. El lugar del
disparo se encuentra en colatitud 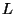 . Probar que al retornar, el
objeto cae hacia el oeste desplazado un distancia
. Probar que al retornar, el
objeto cae hacia el oeste desplazado un distancia
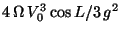 del punto de disparo. En la expresión,
del punto de disparo. En la expresión, 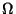 es la velocidad
angular de rotación terrestre y
es la velocidad
angular de rotación terrestre y 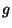 la aceleración gravitatoria
en la superficie en el punto de disparo.
Despreciar el movimiento de la tierra alrededor del sol, como
así tambien los efectos de fricción en la atmósfera.
la aceleración gravitatoria
en la superficie en el punto de disparo.
Despreciar el movimiento de la tierra alrededor del sol, como
así tambien los efectos de fricción en la atmósfera.
Problema 9: Péndulo de Foucault. Determine el efecto de la
rotación de la tierra sobre las pequeñas oscilaciones de un
péndulo. ¿Cuánto rota el plano de oscilación al cabo de un
día?
Fa.M.A.F ©2000
Pedro Pury
2000-12-18