Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Mecánica
Guía N 7: El Hamiltoniano y
las Ecuaciones Canónicas
7: El Hamiltoniano y
las Ecuaciones Canónicas
Problema 1: Escribir el Hamiltoniano y las correspondientes ecuaciones de
Hamilton para una partícula libre en coordenadas cartesianas,
cilíndricas y esféricas.
Problema 2: Escribir el Hamiltoniano y las correspondientes ecuaciones
de Hamilton para una partícula en un potencial central.
Analice el problema de Kepler en esta descripción.
Problema 3: Determinar la función de Hamilton correspondiente al
oscilador anarmónico cuya función de Lagrange es:
Problema 4: Una partícula puede moverse sobre la superficie interna
de un cilindro infinito de radio 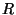 , cuyo eje está ubicado
horizontalmente, en presencia de un campo gravitatorio vertical
homogéneo con aceleración
, cuyo eje está ubicado
horizontalmente, en presencia de un campo gravitatorio vertical
homogéneo con aceleración 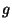 .
.
a) Escribir el Hamiltoniano del sistema.
b) Resolver el problema de pequeñas oscilaciones
correspondiente.
Problema 5: Determinar la función de Hamilton correspondiente a una
partícula en un campo conservativo, en términos de las
coordenadas cartesianas de un sistema que rota uniformemente
alrededor del eje 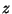 con velocidad angular
con velocidad angular 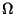 .
¿Cuál es el significado físico del Hamiltoniano en este caso?
.
¿Cuál es el significado físico del Hamiltoniano en este caso?
Problema 6: Para una partícula, calcular los paréntesis de
Poisson formados por:
a) las componentes cartesianas del momento
lineal 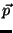 y del momento angular
y del momento angular
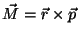 ;
;
b) las componentes cartesianas del momento angular.
Problema 7: Probar que
![$[\vec{f}, \,\vec{n} \cdot \vec{M}] = -\vec{n} \times \vec{f}$](img9.gif) ,
donde
,
donde
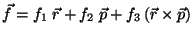 con
con 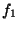 ,
, 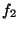 y
y 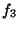 arbitrarios y
arbitrarios y 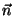 es un versor en la dirección de
es un versor en la dirección de 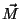 .
.
Problema 8: Mostrar que si el Hamiltoniano y una cantidad 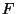 son
constantes de movimiento para un determinado sistema mecánico,
entonces
son
constantes de movimiento para un determinado sistema mecánico,
entonces
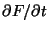 tambien es una constante de
movimiento.
Como ilustración considerar el movimiento de una partícula
libre de masa
tambien es una constante de
movimiento.
Como ilustración considerar el movimiento de una partícula
libre de masa 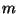 . El Hamiltoniano se conserva y considerar como
constante de movimiento adicional:
. El Hamiltoniano se conserva y considerar como
constante de movimiento adicional:
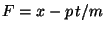 .
Mostrar por cálculo directo que la constante de movimiento
.
Mostrar por cálculo directo que la constante de movimiento
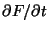 coincide con
coincide con ![$[H,F]$](img20.gif) .
.
Problema 9: Demostrar por cálculo directo que
![$[f,g]_{p,q} = [f,g]_{P,Q}$](img21.gif) , si
, si 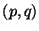 y
y 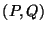 están ligados por
una transformación canónica.
están ligados por
una transformación canónica.
Problema 10: Probar que una rotación en el espacio de fases de un
sistema con un grado de libertad, es una transformación canónica.
Problema 11: Mostrar que la transformación:
es canónica.
Problema 12: Considerar la transformación de coordenadas:
a) Demostrar que 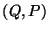 son variables canónicas
si
son variables canónicas
si 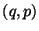 lo son.
lo son.
b) Mostrar que la función que genera esta
transformación es:
Problema 13: Resolver el problema del oscilador armónico lineal
utilizando las variables canónicas 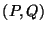 , obtenidas a partir de
la función generatriz:
, obtenidas a partir de
la función generatriz:
Problema 14: ¿Qué condición debe satisfacer la función 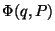 para que sea posible utilizarla como función generatriz de una
transformación canónica? Considerar en particular el ejemplo:
para que sea posible utilizarla como función generatriz de una
transformación canónica? Considerar en particular el ejemplo:
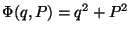 .
.
Problema 15: ¿Qué significado tiene la transformación canónica
originada por la función generatriz:
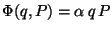 ?
?
Problema 16: Resolver el movimiento de un proyectil puntual en el espacio
bajo la influencia de una fuerza gravitatoria uniforme, usando el
método de Hamilton-Jacobi. Encontrar la ecuación de la
trayectoria y la dependencia de las coordenadas con el tiempo.
Problema 17: Utilizando la ecuación de Hamilton-Jacobi, calcular las
ecuaciones de movimiento y la trayectoria de una partícula en
el campo:
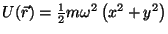 .
.
Fa.M.A.F ©2000
Pedro Pury
2000-12-18