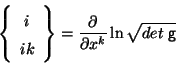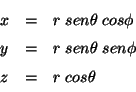Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Métodos Matemáticos de la Física
Guía N 2: Análisis Tensorial
2: Análisis Tensorial
Problema 1: Si
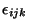 es el símbolo
antisimétrico de Levi-Civita:
es el símbolo
antisimétrico de Levi-Civita:
a) Demostrar que
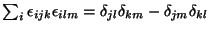 .
.
b) Calcular
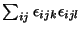
c) Dada la matriz M, calcular:
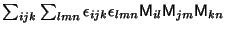
Problema 2: Considere un tensor covariante
simétrico arbitrario 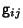 . Mediante
. Mediante 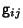 ,
podemos definir una operación de diferenciación covariante.
Demostrar que la derivada covariante de
,
podemos definir una operación de diferenciación covariante.
Demostrar que la derivada covariante de 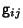 definida de
esta forma se anula.
definida de
esta forma se anula.
Problema 3: Consideremos el símbolo de Christoffel
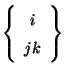 formado con la
ayuda de un tensor covariante simétrico arbitrario
formado con la
ayuda de un tensor covariante simétrico arbitrario 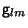 .
Demostrar que:
.
Demostrar que:
Problema 4: Se definen las coordenadas 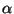 ,
,
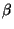 ,
, 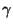 mediante las relaciones:
mediante las relaciones:
donde 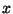 ,
, 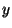 ,
, 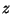 son las coordenadas cartesianas. Dada una
función arbitraria
son las coordenadas cartesianas. Dada una
función arbitraria 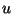 , calcular
, calcular 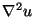 en función de las
derivadas de
en función de las
derivadas de 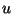 respecto de
respecto de 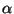 ,
, 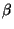 ,
, 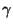 .
.
Problema 5: Se definen las coordenadas 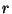 ,
,
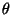 ,
, 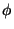 mediante las relaciones:
mediante las relaciones:
donde 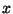 ,
, 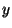 ,
, 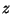 son las coordenadas cartesianas. Dada una
función arbitraria
son las coordenadas cartesianas. Dada una
función arbitraria 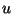 , calcular
, calcular 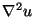 en función de las
derivadas de
en función de las
derivadas de 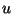 respecto de
respecto de 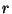 ,
, 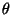 ,
, 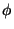 .
.
Fa.M.A.F ©1995
Pedro Pury
2001-02-07
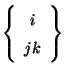 formado con la
ayuda de un tensor covariante simétrico arbitrario
formado con la
ayuda de un tensor covariante simétrico arbitrario