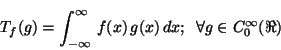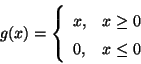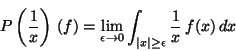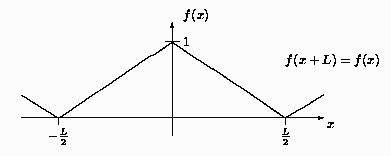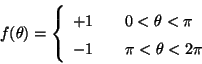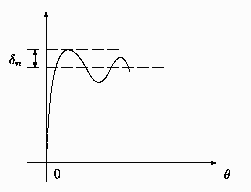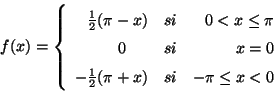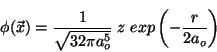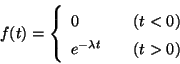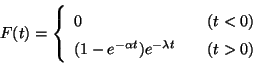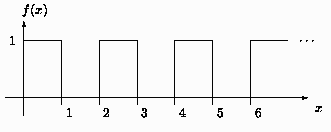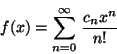Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Métodos Matemáticos de la Física
Guía N 4:
Distribuciones y Transformadas Integrales
4:
Distribuciones y Transformadas Integrales
Problema 1: Sea la distribución
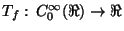 , es decir una funcional
lineal continua tal que:
, es decir una funcional
lineal continua tal que:
Probar que si 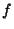 es continua entonces: Soporte(
es continua entonces: Soporte(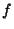 ) =
Soporte(
) =
Soporte(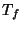 ).
).
Problema 2: ¿Cómo extendería al concepto de
distribución la noción de función par
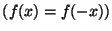 y el de
función impar
y el de
función impar
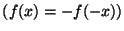 ?. ¿Qué propiedades conserva la
extensión?
?. ¿Qué propiedades conserva la
extensión?
Problema 3: Sea:
Claramente 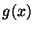 es continua pero no diferenciable (en el sentido
clásico). Encuentre las tres primeras derivadas de
es continua pero no diferenciable (en el sentido
clásico). Encuentre las tres primeras derivadas de 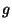 en el
sentido distribucional.
en el
sentido distribucional.
Problema 4: La parte principal, en el sentido de
Cauchy, de una función:
es una distribución. ¿Cómo debe interpretarse la expresión:
Problema 5: Desarrolle la función dibujada a
continuación en una serie de Fourier.
Problema 6: Considere la serie de Fourier para la
función:
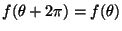 .
.
a) A la derecha de 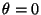 , la suma de los
primeros
, la suma de los
primeros 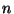 términos de la serie lucen como se detalla en la
figura a continuación. Encontrar
términos de la serie lucen como se detalla en la
figura a continuación. Encontrar 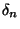 , el ``overshoot'' del
primer máximo.
, el ``overshoot'' del
primer máximo.
b) Mostrar que
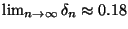 .
Este comportamiento es conocido como fenómeno de Gibbs.
.
Este comportamiento es conocido como fenómeno de Gibbs.
Problema 7: Una función 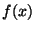 es igual a
es igual a 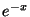 para
para 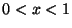 .
.
a) Desarrollle 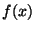 como una serie de Fourier de
la forma
como una serie de Fourier de
la forma
 .
.
b) Desarrollle 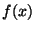 como una serie de Fourier de
período
como una serie de Fourier de
período 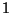 .
.
Problema 8: Un sistema lineal es exitado por una
señal periódica 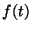 , tal que
, tal que 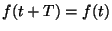 . La respuesta del
sistema es tal que una entrada sinusoidal de frecuencia angular
. La respuesta del
sistema es tal que una entrada sinusoidal de frecuencia angular
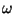 es multiplicada por
es multiplicada por
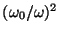 , a menos que
, a menos que
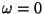 , en cuyo caso no hay salida. La salida puede ser escrita
como:
, en cuyo caso no hay salida. La salida puede ser escrita
como:
Calcule la función 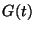 .
.
Problema 9: ¿De qué función es el desarrollo:
una serie de Fourier?
Problema 10: Encontrar la derivada generalizada de la
siguiente función de período 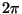 :
:
Verificar que esta función posee el desarrollo en serie de Fourier:
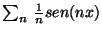 .
Comentario: Derivando término a término esta serie
obtenemos la serie divergente:
.
Comentario: Derivando término a término esta serie
obtenemos la serie divergente:
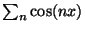 .
Entonces, el concepto de función generalizada nos permite adscribir
un significado a series divergentes en el sentido tradicional.
.
Entonces, el concepto de función generalizada nos permite adscribir
un significado a series divergentes en el sentido tradicional.
Problema 11: Mostrar que:
asumiendo que la ecuación 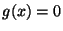 posee una sola raiz en el
intervalo
posee una sola raiz en el
intervalo 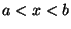 .
.
Problema 12: Evaluar la siguiente expresión:
Problema 13: Calcular la transformada de Fourier de la
función de onda para un electrón 2p en el átomo de hidrógeno:
donde 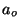 es el radio de Bohr y
es el radio de Bohr y 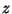 la coordenada rectangular.
la coordenada rectangular.
Problema 14: Un sistema lineal tiene como respuesta
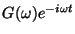 a una señal de entrada
a una señal de entrada
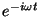 ,
donde
,
donde 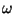 es arbitrario. Si la entrada tiene la forma
particular:
es arbitrario. Si la entrada tiene la forma
particular:
donde 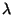 es una constante fija, la salida resultante es:
es una constante fija, la salida resultante es:
donde 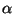 es otra constante fija.
es otra constante fija.
a) Calcular 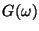 .
.
b) Calcular la respuesta del sistema a la entrada
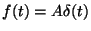 .
.
Problema 15: Calcular la transformada de Laplace
![${\cal L}[f(x)]$](img53.gif) de la función dibujada a continuación:
de la función dibujada a continuación:
Problema 16: Una función 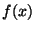 tiene el siguiente
desarrollo en serie:
tiene el siguiente
desarrollo en serie:
Escribir la función
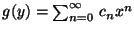 en
forma cerrada en términos de
en
forma cerrada en términos de 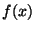 .
.
Problema 17: Utilizando la representación integral:
calcular la transformada de Laplace de 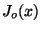 .
.
Problema 18: ¿De qué función es:
la transformada de Laplace?
Problema 19: Tres nucleos radioactivos decaen
sucesivamente en serie, de forma tal que los números 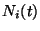 de
cada tipo obedecen las ecuaciones:
de
cada tipo obedecen las ecuaciones:
Si inicialmente 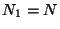 ,
, 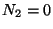 ,
, 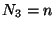 , calcular
, calcular 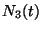 utilizando transformadas de Laplace.
utilizando transformadas de Laplace.
Fa.M.A.F ©1995
Pedro Pury
2001-02-07