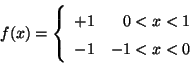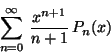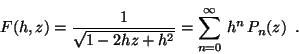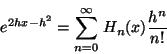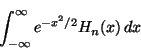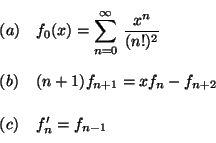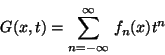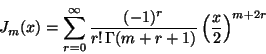Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Métodos Matemáticos de la Física
Guía N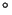 5: Funciones Especiales
5: Funciones Especiales
Problema 1: Sea:
Desarrolle 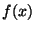 como serie de Polinomios de Legendre
como serie de Polinomios de Legendre 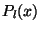 .
.
Problema 2: Utilizando una función generatriz, o
bien por otro método, evalue la serie:
donde 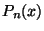 son los polinomios de Legendre.
son los polinomios de Legendre.
Problema 3: Evalue 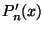 ,
,
a) directamente de la fórmula de Rodrigues:
b) a partir de la función generatriz:
Problema 4: Verifique la siguiente representación
para los armónicos esféricos:
Problema 5: Los polinomios de Hermite 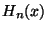 pueden
ser definidos por la función generatriz:
pueden
ser definidos por la función generatriz:
a) Escribir la relación de recursión que conecta:
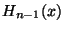 ,
, 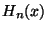 y
y 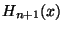 .
.
b) Evaluar:
Problema 6: Considere las funciones 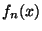 definidas
por:
definidas
por:
Encontrar una función generatriz 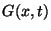 tal que:
tal que:
Problema 7: Sean 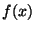 y
y 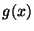 dos soluciones de la
ecuación de Bessel (con el mismo
dos soluciones de la
ecuación de Bessel (con el mismo 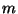 ). Mostrar que su Wronskiano
tiene la forma:
). Mostrar que su Wronskiano
tiene la forma:
Problema 8: Calcular el Wronskiano de 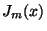 y
y
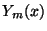 (m arbitrario).
(m arbitrario).
Problema 9: Mostrar que la definición:
de los 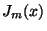 implica que
implica que
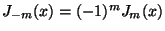 para todo
para todo 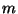 entero.
entero.
Problema 10: Verificar directamente que:
Fa.M.A.F ©1995
Pedro Pury
2001-02-07