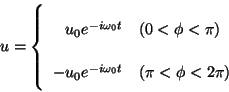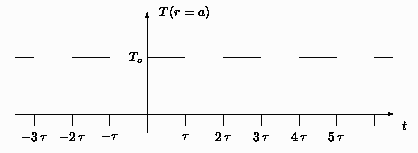Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Métodos Matemáticos de la Física
Guía N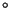 6: Ecuaciones Diferenciales en
Derivadas Parciales
6: Ecuaciones Diferenciales en
Derivadas Parciales
Problema 1: Resuelva las siguientes ecuaciones
diferenciales en derivadas parciales de primer orden, considerando el
problema de valores iniciales especificado:
En el caso b), ¿Hasta que valor del tiempo 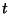 se pueden
extender las soluciones?
Ayudas:
i) Especifique el campo de direcciones
características asociado con cada ecuación.
ii) Considere la curva
se pueden
extender las soluciones?
Ayudas:
i) Especifique el campo de direcciones
características asociado con cada ecuación.
ii) Considere la curva
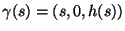 en
en 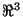 .
Obtenga la curva característica
.
Obtenga la curva característica 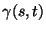 que pasa por cada
que pasa por cada
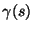 en
en 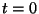 , resolviendo la ecuación diferencial ordinaria
que determina el campo de direcciones características.
, resolviendo la ecuación diferencial ordinaria
que determina el campo de direcciones características.
Problema 2: Considere un círculo de radio 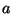 con
centro en el origen de coordenadas. Sean
con
centro en el origen de coordenadas. Sean 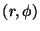 las coordenadas
polares y
las coordenadas
polares y 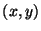 las correspondientes coordenadas rectangulares del
plano. Calcular la solución del problema de Dirichlet (interior)
para la ecuación de Laplace (
las correspondientes coordenadas rectangulares del
plano. Calcular la solución del problema de Dirichlet (interior)
para la ecuación de Laplace (
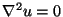 ) con las siguientes
condiciones de contorno:
) con las siguientes
condiciones de contorno:
a) 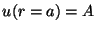
b)
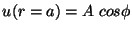
c)
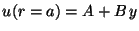
d)
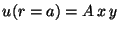
e)
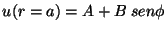
f)
 ;
A, B: ctes.
;
A, B: ctes.
Problema 3: Considere en el problema anterior
condiciones de contorno de Neumann:
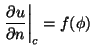 (interior) para los siguientes casos particulares:
(interior) para los siguientes casos particulares:
a) 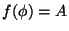
b)
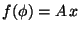
c)
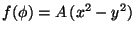
d)
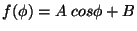
e)
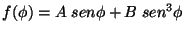
Identifique los problemas incorrectamente formulados.
Problema 4: Determinar la distribución estacionaria
de la temperatura dentro de la capa esférica 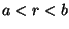 si la esfera
si la esfera
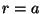 se mantiene a la temperatura
se mantiene a la temperatura 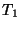 y la esfera
y la esfera 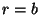 a la
temperatura
a la
temperatura 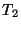 .
.
Problema 5: Calcular la solución de la ecuación de
Poisson en el plano:
dentro del círculo de radio 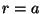 si
si 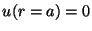 .
.
Problema 6: Resolver el problema de las oscilaciones
transversales propias de una cuerda homogénea de longitud 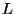 si:
si:
a) Los extremos de la cuerda están fijos
rígidamente.
b) Los estremos de la cuerda están libres.
Es decir
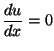 en los extremos de la cuerda.
Esto tiene lugar cuando los extremos de la cuerda están sujetos
mediante anillos (de masas despreciables), que deslizan sin
rozamiento sobre barras paralelas.
en los extremos de la cuerda.
Esto tiene lugar cuando los extremos de la cuerda están sujetos
mediante anillos (de masas despreciables), que deslizan sin
rozamiento sobre barras paralelas.
c) Un extremo de la cuerda está fijo
rígidamente y el otro libre.
d) Los extremos de la cuerda están fijos
elásticamente, es decir que:
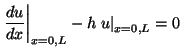 .
.
e) Un extremo de la cuerda está fijo
rígidamente y el otro elásticamente.
f) Un extremo de la cuerda está fijo
elásticamente y el otro está libre.
Problema 7: En los instrumentos musicales de cuerda
percutida (por ejemplo, el piano) las oscilaciones transversales de
la cuerda tensa se generan mediante un golpe, que le da a la cuerda
una velocidad inicial sin desviación inicial. Si el martillo
percutor es plano, rígido y tiene un ancho 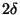 , el perfil
de velocidad inicial de la cuerda estará dado por:
, el perfil
de velocidad inicial de la cuerda estará dado por:
asumiendo que el martillito golpea a una distancia 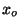 del extremo
de la cuerda y que esta tiene un largo
del extremo
de la cuerda y que esta tiene un largo 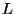 .
.
a) Determine las oscilaciones de la cuerda 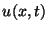 para todo
para todo 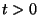 , asumiendo que
, asumiendo que
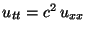 .
.
b) Para la energía de la cuerda oscilando se
tiene la expresión:
donde la densidad 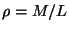 , si M es la masa de la cuerda. Calcule
la energía asociada con cada modo de oscilación o armónico.
, si M es la masa de la cuerda. Calcule
la energía asociada con cada modo de oscilación o armónico.
c) Determine en que puntos de la cuerda 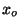 la
percusión no excita el m-ésimo modo de oscilación.
la
percusión no excita el m-ésimo modo de oscilación.
d) Bajo la razonable aproximación 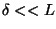 determine cuál es el armónico que más resuena (es decir que
posee mayor energía) si se percute la cuerda a una distancia
determine cuál es el armónico que más resuena (es decir que
posee mayor energía) si se percute la cuerda a una distancia
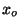 de uno de sus extremos.
de uno de sus extremos.
Problema 8: Calcular las oscilaciones propias de una
membrana circular,
a) con la frontera fija rígidamente.
b) con la frontera libre.
Problema 9: Calcular la frecuencia más baja de
oscilación de una onda acústica en una esfera hueca de radio 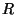 .
La condición de contorno es:
.
La condición de contorno es:
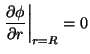 y
y 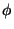 obedece la ecuación de ondas homogénea.
obedece la ecuación de ondas homogénea.
Problema 10: La cantidad 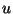 satisface la ecuación
de ondas homogénea dentro de un cilindro de radio
satisface la ecuación
de ondas homogénea dentro de un cilindro de radio 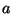 , con la
condición de contorno
, con la
condición de contorno 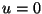 en las paredes del cilindro. En el
extremo
en las paredes del cilindro. En el
extremo 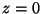 tiene que
tiene que
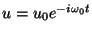 ; es decir, se
están enviando ondas a lo largo del tubo con diferentes
distribuciones espaciales (modos). Encuentre la velocidad de fase
del modo fundamental como función de la frecuencia
; es decir, se
están enviando ondas a lo largo del tubo con diferentes
distribuciones espaciales (modos). Encuentre la velocidad de fase
del modo fundamental como función de la frecuencia 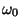 e
interprete el resultado para pequeños valores de
e
interprete el resultado para pequeños valores de 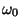 .
.
Problema 11: Encontrar las frecuencias de oscilación
más bajas de un parche de tambor en forma de triángulo
isósceles recto de lados 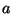 ,
, 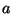 ,
, 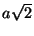 .
.
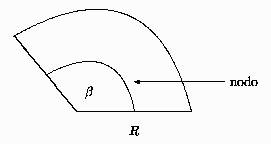
Problema 12: Considere un parche de tambor con la
forma de un sector circular de radio 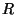 y ángulo
y ángulo 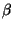 .
.
a) ¿Cuál modo es el ilustrado en la figura?.
Dé su respuesta para 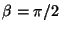 ,
, 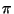 ,
, 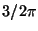 .
.
b) Esquematice en un gráfico las frecuencias de la
primer media docena de modos como funciones de 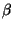 .
.
Problema 13: La ecuación que describe las ondas
elásticas en un medio isotrópico es:
donde 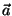 mide los desplazamientos desde el equilibrio,
mide los desplazamientos desde el equilibrio, 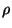 es la densidad, y
es la densidad, y 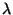 y
y 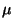 son las constantes elásticas
del medio. Encuentre la frecuencia más baja de oscilación de una
esfera elástica isotrópica de radio
son las constantes elásticas
del medio. Encuentre la frecuencia más baja de oscilación de una
esfera elástica isotrópica de radio 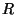 , dado que:
a)
, dado que:
a)
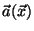 es de la forma
es de la forma
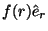 ,
y
b) la condición de contorno en
,
y
b) la condición de contorno en 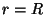 es:
es:
Con el fin de calcular un número concreto, considere al final
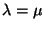 .
.
Problema 14: En el exterior de un cilindro
infinitamente largo de radio 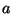 la función potencial
la función potencial
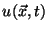 satisface la ecuación de ondas. El cilindro se
encuentra dividido longitudinalmente, y sobre su superficie
satisface la ecuación de ondas. El cilindro se
encuentra dividido longitudinalmente, y sobre su superficie
Calcular 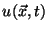 fuera del cilindro, si sólo existen
ondas salientes para
fuera del cilindro, si sólo existen
ondas salientes para 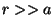 .
.
Problema 15: Asuma que la densidad de neutrones 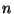 dentro del
dentro del 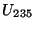 obedece la ecuación diferencial:
obedece la ecuación diferencial:
a) Encontrar el radio crítico 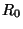 para el cual
una esfera de
para el cual
una esfera de 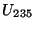 con un radio igual o mayor a dicho valor es
inestable, es decir que densidad de neutrones en su interior crece
exponencialmente con el tiempo.
con un radio igual o mayor a dicho valor es
inestable, es decir que densidad de neutrones en su interior crece
exponencialmente con el tiempo.
b) Suponga dos hemisferios de 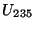 tales que se
encuentren en el límite de estabilidad. Si se juntan para formar
una esfera, esta resulta inestable, y se cumple que:
tales que se
encuentren en el límite de estabilidad. Si se juntan para formar
una esfera, esta resulta inestable, y se cumple que:
Encontrar la constante de tiempo 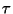 de la explosión resultante.
de la explosión resultante.
Problema 16: Una esfera de radio 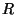 está
uniformemente a temperatura
está
uniformemente a temperatura 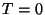 . En el instante
. En el instante 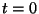 , es sumergida
en un baño líquido a temperatura constante
, es sumergida
en un baño líquido a temperatura constante 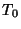 . Calcular la
subsecuente distribución de temperatura
. Calcular la
subsecuente distribución de temperatura 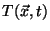 dentro de la
esfera. (Sea
dentro de la
esfera. (Sea 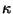 = conductividad térmica / (densidad
= conductividad térmica / (densidad 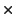 calor específico)).
calor específico)).
Problema 17: La temperatura en una esfera homogénea
de radio 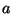 obedece la ecuación de difusión con constante
obedece la ecuación de difusión con constante
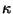 . Por acciones externas, la temperatura de la superficie de
la esfera es forzada a comportarse según lo ilustrado en la figura.
Caltular la temperatura
. Por acciones externas, la temperatura de la superficie de
la esfera es forzada a comportarse según lo ilustrado en la figura.
Caltular la temperatura 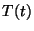 en el centro de la esfera.
Las alteraciones se extienden para
en el centro de la esfera.
Las alteraciones se extienden para 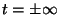 .
.
Problema 18: Encontrar los tres autovalores más
pequeños de la ecuación de Schrödinger para una partícula
confinada en una caja cilíndrica de radio 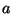 y altura
y altura 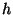 .
.
Problema 19: Utilice la transformada coseno con
respecto a 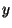 para calcular la distribución de temperatura
estacionaria en un sólido semi-infinito (
para calcular la distribución de temperatura
estacionaria en un sólido semi-infinito (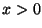 ) cuando la
temperatura en la superficie (
) cuando la
temperatura en la superficie (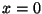 ) se mantiene constante e igual a
la unidad para
) se mantiene constante e igual a
la unidad para 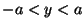 , y cero fuera de esa franja.
, y cero fuera de esa franja.
Problema 20: Un alambre recto de radio 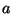 es
sumergido en un volumen infinito de líquido. Inicialmente el
alambre y el líquido tienen temperatura
es
sumergido en un volumen infinito de líquido. Inicialmente el
alambre y el líquido tienen temperatura 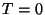 . En
. En 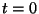 , el
alambre es súbitamente llevado a la temperatura
, el
alambre es súbitamente llevado a la temperatura 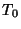 y mantenido
en ella. Encuentre la transformada de Laplace
y mantenido
en ella. Encuentre la transformada de Laplace 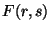 de la
distribución de temperatura
de la
distribución de temperatura 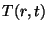 resultante en el líquido.
resultante en el líquido.
Problema 21: Utilice transformadas de Fourier para
calcular el movimiento de una cuerda estirada, infinitamente larga,
con desplazamientos iniciales dados
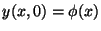 y velocidad
inicial nula. Los desplazamientos satisfacen la ecuación de ondas
homogénea.
y velocidad
inicial nula. Los desplazamientos satisfacen la ecuación de ondas
homogénea.
Problema 22: Las funciones de Green pueden calcularse
para ecuaciones diferenciales homogéneas con condiciones de
contorno inhomogéneas. Para ilustrar esto, considere la ecuación
de Helmholtz:
dentro del círculo de radio 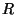 , con la condición de contorno
dada:
, con la condición de contorno
dada:
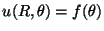 . La solución puede escribirse como:
. La solución puede escribirse como:
Calcule
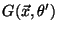 .
.
Fa.M.A.F ©1995
Pedro Pury
2001-02-07
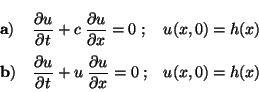
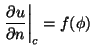 (interior) para los siguientes casos particulares:
(interior) para los siguientes casos particulares:
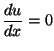 en los extremos de la cuerda.
Esto tiene lugar cuando los extremos de la cuerda están sujetos
mediante anillos (de masas despreciables), que deslizan sin
rozamiento sobre barras paralelas.
en los extremos de la cuerda.
Esto tiene lugar cuando los extremos de la cuerda están sujetos
mediante anillos (de masas despreciables), que deslizan sin
rozamiento sobre barras paralelas.
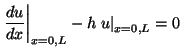 .
.
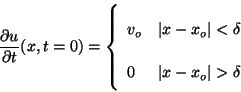
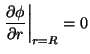 y
y