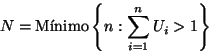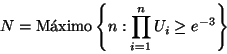Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Guía N 2: Números Aleatorios
2: Números Aleatorios
Problema 1: Para el estudio mediante simulación es necesario generar
muchos números aleatorios en la computadora. Estos corresponden a
variables aleatorias uniformemente distribuídas en el
intervalo
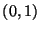 . Existen en la literatura varias rutinas
optimizadas para generar enormes cantidades de números
seudo-aleatorios con velocidad razonable.
Se propone aprender a implementar las siguientes rutinas:
. Existen en la literatura varias rutinas
optimizadas para generar enormes cantidades de números
seudo-aleatorios con velocidad razonable.
Se propone aprender a implementar las siguientes rutinas:
a) RAN2. Ver
``Numerical Recipes: The Art of Scientific Computing'',
W. H. Press, B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling
(Cambridge, 1986). Esta referencia está disponible
online.
b) MZRAN. Ver
``Some Portable Very-Long-Period Random Number Generators'',
G. Marsaglia and A. Zaman,
Computers in Physics 8(1), 117 (1994).
Para ambos generadores existen implementaciones en C
y FORTRAN.
Problema 2: Calcule exactamente el valor de las siguientes integrales.
Mediante una simulación de Monte Carlo, calcule a su vez un valor
aproximado y compare con el valor exacto.
a)
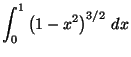
b)
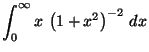
c)
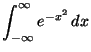
d)
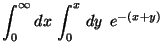
Ayuda: Sea:
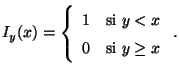 Utilice esta función para igualar la integral del item d) a
otra cuyos términos vayan de
Utilice esta función para igualar la integral del item d) a
otra cuyos términos vayan de 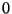 a
a 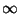 .
.
Problema 3: Para
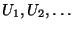 variables aleatorias uniformemente
distribuídas en el intervalo
variables aleatorias uniformemente
distribuídas en el intervalo 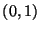 , se define:
, se define:
Es decir, 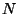 es igual a la cantidad de números aleatorios que
deben sumarse para exeder a
es igual a la cantidad de números aleatorios que
deben sumarse para exeder a 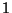 .
.
a) Estimar ![$E[N]$](img14.gif) generando
generando 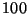 valores de
valores de 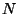 .
.
b) Estimar ![$E[N]$](img14.gif) generando
generando 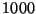 valores de
valores de 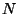 .
.
c) Estimar ![$E[N]$](img14.gif) generando
generando 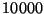 valores de
valores de 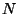 .
.
d) Calcular el valor exacto de ![$E[N]$](img14.gif) .
.
Problema 4: Para
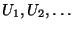 números aleatorios, se define:
números aleatorios, se define:
donde:
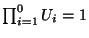 . Mediante simulación
determinar:
. Mediante simulación
determinar:
a) ![$E[N]$](img14.gif)
b) 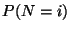 para
para
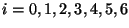 .
.
Fa.M.A.F ©2001-2002
Pedro Pury
2001-03-07
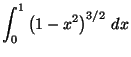
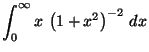
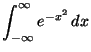
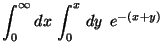
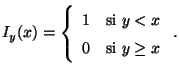 Utilice esta función para igualar la integral del item d) a
otra cuyos términos vayan de
Utilice esta función para igualar la integral del item d) a
otra cuyos términos vayan de