Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Guía N 5: Análisis Estadístico de
Datos Simulados
5: Análisis Estadístico de
Datos Simulados
Problema 1: Generar 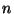 valores de una variable aleatoria normal
estándar de manera tal que se cumplan las condiciones:
valores de una variable aleatoria normal
estándar de manera tal que se cumplan las condiciones: 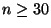 y
y
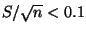 , siendo
, siendo 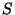 la desviación estándar muestral
de los
la desviación estándar muestral
de los 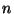 datos generados.
datos generados.
a) ¿Cuál es el número esperado de datos que deben
generarse para cumplir las condiciones?
b) ¿Cuál es el número de datos generados
efectivamente?
c) ¿Cuál es la media muestral de los datos
generados?
d) ¿Cuál es la varianza muestral de los datos
generados?
e) Comente los resultados de los items (c) y (d).
¿Son sorprendentes?
Problema 2: Estimar mediante el método de Monte Carlo la integral
Generar al menos 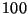 valores y detenerse cuando la desviación
estándar del estimador sea menor que
valores y detenerse cuando la desviación
estándar del estimador sea menor que 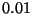 .
.
Problema 3: Para
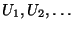 variables aleatorias uniformemente
distribuídas en el intervalo
variables aleatorias uniformemente
distribuídas en el intervalo 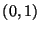 , se define:
, se define:
Es decir, 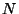 es igual a la cantidad de números aleatorios que
deben sumarse para exeder a
es igual a la cantidad de números aleatorios que
deben sumarse para exeder a 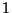 .
Como se mostró en el Problema 3 de la Guía N
.
Como se mostró en el Problema 3 de la Guía N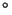 2,
2,
![$E[N] = e$](img14.gif) .
Calcular la varianza del estimador
.
Calcular la varianza del estimador ![$E[N]$](img15.gif) correspondiente
a
correspondiente
a 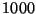 ejecuciones de la simulación y dar una estimación de
ejecuciones de la simulación y dar una estimación de 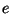 mediante un intervalo de confianza de
mediante un intervalo de confianza de 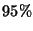 .
.
Problema 4: Considere una sucesión de números aleatorios y sea 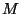 el
primero que es menor que su predecesor. Es decir,
el
primero que es menor que su predecesor. Es decir,
a) Justificar que
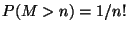 ,
, 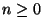 .
.
b) Utilizar la identidad
para mostrar que ![$E[M] = e$](img24.gif) .
.
c) Utilizar el resultado del item anterior para
estimar 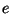 mediante
mediante 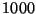 ejecuciones de una simulación.
ejecuciones de una simulación.
d) Calcular la varianza del estimador del item (c)
y dar una estimación de 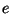 mediante un intervalo de confianza
de
mediante un intervalo de confianza
de 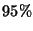 .
.
Problema 5: Estimar 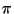 sorteando puntos uniformemente distribuídos
en el cuadrado cuyos vértices son:
sorteando puntos uniformemente distribuídos
en el cuadrado cuyos vértices son: 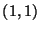 ,
, 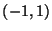 ,
, 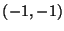 ,
,
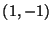 , y contabilizando la fracción que cae dentro del
círculo inscripto de radio
, y contabilizando la fracción que cae dentro del
círculo inscripto de radio 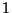 .
Obtener un intervalo de ancho menor que
.
Obtener un intervalo de ancho menor que 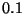 , el cual
contenga a
, el cual
contenga a 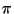 con el
con el 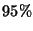 de confianza.
¿Cuántas ejecuciones son necesarias?
de confianza.
¿Cuántas ejecuciones son necesarias?
Problema 6: Sean
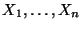 variables aleatorias independientes
e idénticamente distribuídas con media
variables aleatorias independientes
e idénticamente distribuídas con media 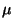 desconocida.
Para
desconocida.
Para 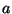 y
y 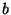 constantes dadas,
constantes dadas, 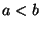 , nos interesa estimar
, nos interesa estimar
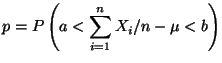 .
.
a) Explicar como utilizar el método ``bootstrap''
para estimar 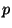 .
.
b) Estimar 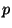 asumiendo que para
asumiendo que para 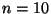 , los valores
de las variables
, los valores
de las variables 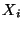 resultan 56, 101, 78, 67, 93, 87, 64, 72, 80
y 69. Sean
resultan 56, 101, 78, 67, 93, 87, 64, 72, 80
y 69. Sean 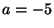 y
y 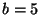 .
.
Problema 7: Sean
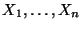 variables aleatorias independientes
e idénticamente distribuídas con varianza
variables aleatorias independientes
e idénticamente distribuídas con varianza 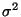 desconocida.
Se planea estimar
desconocida.
Se planea estimar 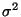 mediante la varianza muestral
mediante la varianza muestral
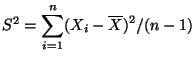 .
Si
.
Si 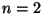 ,
, 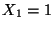 y
y 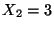 , ¿cuál es la estimación
``bootstrap'' de
, ¿cuál es la estimación
``bootstrap'' de 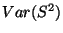 ?
?
Problema 8: Considerar un sistema con un único servidor en el cual los
clientes potenciales llegan de acuerdo con un proceso de Poisson de
razón 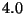 . Un cliente potencial entrará al sistema sólo si
hay tres o menos clientes en el sistema al momento de su llegada.
El tiempo de servicio de cada cliente está distribuído según
una exponencial de parámetro
. Un cliente potencial entrará al sistema sólo si
hay tres o menos clientes en el sistema al momento de su llegada.
El tiempo de servicio de cada cliente está distribuído según
una exponencial de parámetro 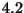 .
Despues del instante
.
Despues del instante 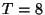 no entran más clientes al sistema (los
tiempos están dados en horas). Realizar un estudio de simulación
para estimar el tiempo promedio que un cliente pasa en el sistema.
Aplicar el método ``bootstrap'' para estudiar el error cuadrático
medio de su estimador.
no entran más clientes al sistema (los
tiempos están dados en horas). Realizar un estudio de simulación
para estimar el tiempo promedio que un cliente pasa en el sistema.
Aplicar el método ``bootstrap'' para estudiar el error cuadrático
medio de su estimador.
Fa.M.A.F ©2001-2002
Pedro Pury
2001-04-26
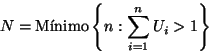
![\begin{displaymath}
E[M] = \sum_{n=0}^{\infty} P(M > n)
\end{displaymath}](img23.gif)
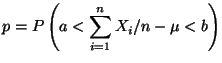 .
.
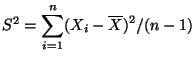 .
Si
.
Si