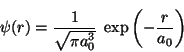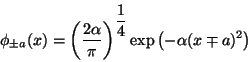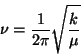Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Física Moderna II
Guía N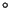 4: Moléculas
4: Moléculas
Problema 1: Calcule la energía del estado
fundamental del H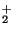 . Construya los estados electrónicos
moleculares utilizando las adecuadas combinaciones lineales
(simétrica y antisimétrica) del estado fundamental del H:
. Construya los estados electrónicos
moleculares utilizando las adecuadas combinaciones lineales
(simétrica y antisimétrica) del estado fundamental del H:
Exprese la energía de la forma:
donde 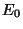 es la energía del estado fundamental del H, el
segundo término corresponde a la enegía de repulsión
coulombiana entre los protones. Describa explícitamente el
último término y discuta las condiciones de estabilidad para la
mólecula.
es la energía del estado fundamental del H, el
segundo término corresponde a la enegía de repulsión
coulombiana entre los protones. Describa explícitamente el
último término y discuta las condiciones de estabilidad para la
mólecula.
Problema 2: Los dos protones en la molécula H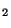 están separados una distancia de
están separados una distancia de 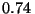 Å. ¿Cuál es la carga
puntual negativa que debe colocarse en el punto que equidista de los
protones para tener la energía de ligadura observada en el
sistema (
Å. ¿Cuál es la carga
puntual negativa que debe colocarse en el punto que equidista de los
protones para tener la energía de ligadura observada en el
sistema (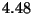 eV)?
eV)?
Problema 3:
a) Explique porqué el ión de H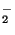 tiene una
energía de disociación menor que el ión He
tiene una
energía de disociación menor que el ión He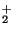 .
.
b) ¿Existe un estado estable para la molécula de
He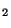 ? Explique.
? Explique.
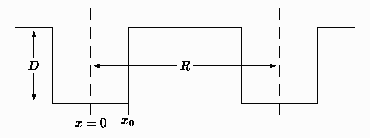
Problema 4: Considere el potencial unidimensional
correspondiente a dos pozos cuadrados profundos, idénticos, de
ancho 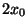 y separados por una distancia
y separados por una distancia 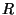 (
(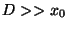 ):
):
a) Para el caso en que 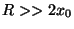 grafique
cualitativamente las funciones de onda correspondientes a un
electrón en el estado fundamental de ese potencial, y discuta sus
características y las energías asociadas con cada una de
ellas.
grafique
cualitativamente las funciones de onda correspondientes a un
electrón en el estado fundamental de ese potencial, y discuta sus
características y las energías asociadas con cada una de
ellas.
b) Grafique las funciones de onda del estado
fundamental y primer exitado, correspondientes a la situación
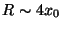 .
.
c) Considere que 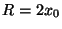 . Grafique las dos
primeras funciones de onda para esta situación, y establezca cuál
es la razón entre las energías asociadas con cada función.
. Grafique las dos
primeras funciones de onda para esta situación, y establezca cuál
es la razón entre las energías asociadas con cada función.
d) Grafique en forma esquemática la energía
asociada con cada función de onda en función de 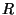 .
.
Problema 5: Una partícula de masa 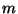 se mueve en
el potencial ``doble oscilador'':
se mueve en
el potencial ``doble oscilador'':
Cuando la separación 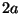 entre los mínimos del potencial es lo
suficientemente grande, una buena aproximación de las dos
autofunciones para los estados de energía más baja esta dada
por:
entre los mínimos del potencial es lo
suficientemente grande, una buena aproximación de las dos
autofunciones para los estados de energía más baja esta dada
por:
donde
es la autofunción del oscilador armónico simple centrado en
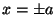 , con
, con
a) Utilizando las autofunciones aproximadas, mostrar
que las energías
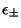 de los dos autoestados más
bajos pueden escribirse según:
de los dos autoestados más
bajos pueden escribirse según:
donde
con
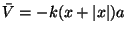 .
.
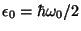 es
la energía del estado fundamental del oscilador armónico
simple.
es
la energía del estado fundamental del oscilador armónico
simple.
b) Evaluar 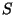 y verificar que la separación de
energía entre los dos primeros estados es proporcional a
y verificar que la separación de
energía entre los dos primeros estados es proporcional a
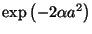 .
.
Problema 6: Demostrar que las cuatro funciones de onda
híbridas 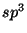 son ortogonales. Hacer lo mismo con las funciones
de onda
son ortogonales. Hacer lo mismo con las funciones
de onda 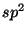 .
.
Problema 7: Discutir la estructura de las siguientes
moléculas: a) C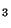 H
H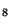 , b) C
, b) C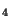 H
H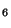 ,
c) C
,
c) C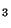 H
H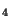 y d) CO
y d) CO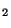 .
.
Problema 8: El momento dipolar eléctrico de H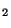 O
es
O
es 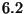 x
x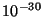 mC. Calcular el momento dipolar
correspondiente a cada unión O--H. Si la longitud de esta
unión es de
mC. Calcular el momento dipolar
correspondiente a cada unión O--H. Si la longitud de esta
unión es de 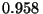 Å, ¿Qué fracción del electrón del
átomo de hidrógeno a sido transferida al átomo de oxígeno?
Å, ¿Qué fracción del electrón del
átomo de hidrógeno a sido transferida al átomo de oxígeno?
Problema 9:
a) Demostrar que el momento de inercia de una
molécula diatómica respecto a un eje normal a la línea que
une a los núcleos y que pasa poe el centro de masa es
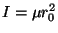 , donde
, donde 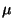 es la masa reducida y
es la masa reducida y 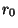 la distancia
internuclear.
la distancia
internuclear.
b) Demostrar que la frecuencia de oscilación
armónica de dos masas 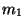 y
y 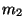 que interactúan con una
constante elástica
que interactúan con una
constante elástica 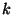 es:
es:
Problema 10: Explicar porqué no se observa en el
espectro de rotación de la molécula de H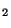 , las transiciones
correspondientes a la rotación alrededor de un eje que pasa por el
centro de los núcleos.
, las transiciones
correspondientes a la rotación alrededor de un eje que pasa por el
centro de los núcleos.
Problema 11: Los momentos principales de inercia de
una molécula son respectivamente:
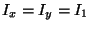 y
y 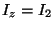 .
a) Demostrar que considerando la moécula como un
cuerpo rígido, la energía rotacional puede expresarse según:
.
a) Demostrar que considerando la moécula como un
cuerpo rígido, la energía rotacional puede expresarse según:
b) Calcular los niveles cuánticos de energía
rotacional si i) 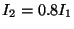 , ii)
, ii) 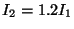 .
c) Representar gráficamente estos niveles en
unidades de
.
c) Representar gráficamente estos niveles en
unidades de
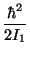 .
.
Problema 12: La molécula diatómica no es
rigurosamente rígida, por lo que la distancia internuclear
aumenta a medida que aumenta el momento angular de la molécula.
a) ¿Cómo afecta este estiramiento los niveles
rotacionales?
b) Una expresión empírica para la energía
rotacional es:
donde 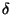 es una constante de estiramiento. Obtener una
expresión para las correspondientes frecuencias de transición
entre niveles rotacionales. Verificar si este efecto de estiramiento
está presente en el espectro rotacional de absorción del HCl en
fase gaseosa.
es una constante de estiramiento. Obtener una
expresión para las correspondientes frecuencias de transición
entre niveles rotacionales. Verificar si este efecto de estiramiento
está presente en el espectro rotacional de absorción del HCl en
fase gaseosa.
Problema 13: Explicar porqué la separación entre
los niveles de energía vibracionales de las moléculas es un
poco menor en un estado electrónico exitado que en el nivel
electrónico fundamental.
Fa.M.A.F ©1995
Pedro Pury
2001-02-13