Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Física Moderna II
Guía N 5: Modelo del Electrón Libre
5: Modelo del Electrón Libre
Problema 1: Distribución de Poisson
En el modelo de Drude la probabilidad de que un electrón
sufra una colisión en un intervalo infinitesimal 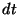 es
es
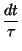 .
.
a) Mostrar que para un electrón tomado al azar en un
instante dado, la probabilidad de no haber sufrido ninguna colisión
durante los 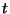 segundos precedentes es
segundos precedentes es 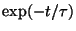 . Mostrar que
la probabilidad de no sufrir ninguna colisión durante los
próximos
. Mostrar que
la probabilidad de no sufrir ninguna colisión durante los
próximos 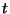 segundos es la misma.
segundos es la misma.
b) Mostrar que la probabilidad de que el intervalo de
tiempo entre dos colisiones sucesivas de un electrón esté entre
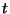 y
y 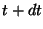 es
es
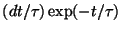 .
.
c) Mostrar que como consecuencia de a), en
cualquier instante, el tiempo medio transcurrido desde la última
colisión o el que trancurrirá hasta la próxima colisión es
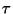 .
.
d) Mostrar que como consecuencia de b), el
tiempo medio entre colisiones sucesivas de un electrón es 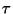 .
.
Usando indiscriminadamente el resultado del item c),
podemos concluir que, en cualquier instante, el tiempo medio 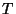 entre la última y la próxima colisión es
entre la última y la próxima colisión es 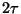 .
Esta apreciación condujo a una famosa paradoja y es el origen del
error cometido por Drude en el cálculo de las conductividades en
los metales.
.
Esta apreciación condujo a una famosa paradoja y es el origen del
error cometido por Drude en el cálculo de las conductividades en
los metales.
Problema 2: Efecto de calentamiento Joule
Considere un metal a temperatura uniforme en un campo
eléctrico estático y uniforme 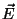 . Un electrón sufre una
colisión y, tras un intervalo
. Un electrón sufre una
colisión y, tras un intervalo 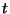 , una segunda colisión.
En el modelo de Drude la energía no es conservada durante las
colisiones, ya que la velocidad media de un electrón que emerge de
una colisión no depende de la energía que éste adquirió
bajo la acción del campo desde la colisión precedente.
, una segunda colisión.
En el modelo de Drude la energía no es conservada durante las
colisiones, ya que la velocidad media de un electrón que emerge de
una colisión no depende de la energía que éste adquirió
bajo la acción del campo desde la colisión precedente.
a) Muestre que la energía media perdida
(entregada a los iones) en la segunda de dos colisiones separadas por
un intervalo de tiempo 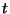 , es
, es 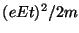 . (El promedio se toma
sobre las posibles direcciones en que el electrón emerge de la
primera colisión).
. (El promedio se toma
sobre las posibles direcciones en que el electrón emerge de la
primera colisión).
b) Muestre que la energía media cedida a los
iones por electrón y por colisión es 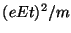 , y por lo
tanto la pérdida media por unidad de volumen y tiempo es
, y por lo
tanto la pérdida media por unidad de volumen y tiempo es
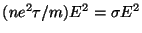 . Deduzca que la potencia disipada
en un alambre de longitud
. Deduzca que la potencia disipada
en un alambre de longitud 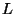 y sección transversal
y sección transversal 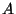 es
es 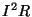 ,
donde
,
donde 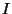 es la corriente total y
es la corriente total y 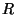 la resistencia del alambre.
la resistencia del alambre.
Problema 3: Conductividad elécrica ac
a) Usando la ecuación de movimiento clásica para
los electrones en un metal, bajo la acción de un campo eléctrico
externo 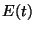 :
:
donde 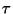 es el tiempo de relajación, muestre que la
conductividad eléctrica ac a frecuencia
es el tiempo de relajación, muestre que la
conductividad eléctrica ac a frecuencia 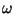 es:
es:
donde
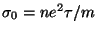 es la conductividad eléctrica
dc.
es la conductividad eléctrica
dc.
b) Grafique las componentes real e imaginaria de la
conductividad ac como funciones de la frecuencia 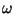 ; y
grafique tambien la componente imaginaria como función de la
componente real. Indique como se recorre esta última curva cuando
se barre en frecuencia (
; y
grafique tambien la componente imaginaria como función de la
componente real. Indique como se recorre esta última curva cuando
se barre en frecuencia (
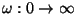 ).
).
Problema 4: Densidades de niveles y de estados
a) Calcule la densidad de niveles cuánticos en el
espacio 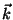 para un gas de electrones libres contenidos en:
para un gas de electrones libres contenidos en:
i) una caja unidimensional de longitud 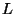 .
.
ii) una caja bidimensional cuadrada de lado 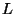 .
.
iii) una caja tridimensional cúbica de arista 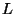 .
.
b) Calcule la densidad de estados en función de la
energía 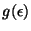 para los tres casos. Analize e interprete
el comportamiento para
para los tres casos. Analize e interprete
el comportamiento para
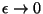 .
.
Problema 5: 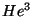 líquido
El átomo de
líquido
El átomo de 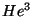 tiene spin
tiene spin 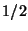 y por lo tanto es un
fermión. La densidad de estados del
y por lo tanto es un
fermión. La densidad de estados del 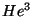 líquido es de
líquido es de
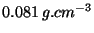 cerca del cero absoluto. Calcule la energía de
Fermi
cerca del cero absoluto. Calcule la energía de
Fermi 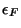 y la temperatura de Fermi
y la temperatura de Fermi 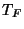 . Compare con un
gas de electrones libres.
. Compare con un
gas de electrones libres.
Problema 6: Susceptibilidad de Pauli
Analize la contribución del spin de los electrones de
conducción a la susceptibilidad magnética de un metal (a 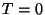 ).
Para ello considere un campo magnético aplicado
).
Para ello considere un campo magnético aplicado 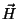 y
descomponga la densidad de estados total
y
descomponga la densidad de estados total 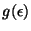 como suma de
una
como suma de
una
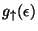 de electrones con spin paralelo al campo
y una
de electrones con spin paralelo al campo
y una
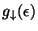 de electrones con spin antiparalelo.
Escriba la magnetización
de electrones con spin antiparalelo.
Escriba la magnetización 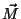 en función del número de
spines up y down; analize cuanto vale ahora la energía de un
electrón y como se llenan los estados hasta el nivel de Fermi.
Tenga en cuenta que aún para campos muy grandes (
en función del número de
spines up y down; analize cuanto vale ahora la energía de un
electrón y como se llenan los estados hasta el nivel de Fermi.
Tenga en cuenta que aún para campos muy grandes (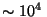 Gauss)
la energía magnética
Gauss)
la energía magnética 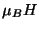 es sólo del orden de
es sólo del orden de
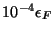 .
Obtenga entonces una relación entre
.
Obtenga entonces una relación entre 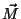 y
y 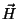 y calcule
la susceptibilidad
y calcule
la susceptibilidad
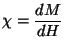 .
.
Fa.M.A.F ©1995
Pedro Pury
2001-02-13
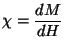 .
.