Guía N
|
Problema 8:
Una esfera sólida de vidrio cuyo radio es |
![\begin{picture}(44.00,14.00)
\put(27.00,7.00){\circle{14.00}}
\put(27.00,14.00...
...box(0,0)[bc]{plateado}}
\put(13.00,4.00){\makebox(0,0)[cc]{$2R$}}
\end{picture}](img35.gif)
|
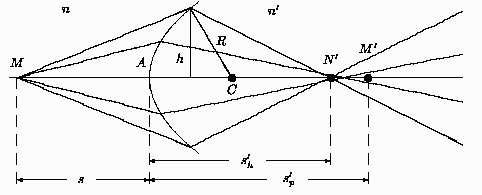
![\begin{picture}(120.00,55.33)
\put(0.00,30.00){\line(1,0){120.00}}
\bezier{264...
...makebox(0,0)[cc]{$l$}}
\put(73.33,37.33){\makebox(0,0)[cl]{$l'$}}
\end{picture}](img57.gif)
![\begin{displaymath}
\frac{n}{s} + \frac{n'}{s'_h} = \frac{n'-n}{R} + \frac{h^2}...
...c{n'}{s'} \left( \frac{1}{s'} - \frac{1}{R} \right)^2 \right]
\end{displaymath}](img63.gif)
![\begin{displaymath}
\frac{n}{s} + \frac{n'}{s'_h} = \frac{n'-n}{R} +
\left[
...
...ght)^2
\left( \frac{1}{R} + \frac{n'+n}{ns} \right)
\right]
\end{displaymath}](img66.gif)
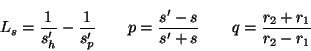
![\begin{picture}(123.00,55.00)
\put(0.00,30.00){\line(1,0){120.00}}
\bezier{180...
...0){\vector(1,0){4.00}}
\put(109.00,13.00){\makebox(0,0)[cc]{AEL}}
\end{picture}](img73.gif)
|
Problema 16:
Dispersión de la Luz en Superficies Refringentes
Se conoce que por refracción es posible separar un haz de luz blanca en sus colores componentes. Se define el poder dispersor de una superficie ( |
![\begin{picture}(70.00,50.00)
\put(0.00,30.00){\line(1,0){70.00}}
\put(20.00,50...
...ebox(0,0)[cc]{$n_D$}}
\put(57.00,15.00){\makebox(0,0)[cc]{$n_C$}}
\end{picture}](img83.gif)
|
| Crown (LBC-1) | |||
| Flint (DF-2) |