Guía N
| Problema 6: En la figura se muestra en tres instantes de tiempo sucesivos, el mismo máximo de una onda sinusoidal. Escribir una expresión para la onda. Determinar la longitud de onda, velocidad, frecuencia y período. |
![\begin{picture}(140.00,115.00)
\put(10.00,0.00){\vector(0,1){35.00}}
\put(10.0...
...x(0,0)[lc]{$z\,$(nm)}}
\put(140.00,15.00){\makebox(0,0)[cc]{$z$}}
\end{picture}](img16.gif)
|
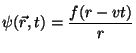 es una solución de la ecuación de onda tridimensional; y que
corresponde a una perturbación esférica centrada en el origen,
que se mueve alejándose del origen con velocidad
es una solución de la ecuación de onda tridimensional; y que
corresponde a una perturbación esférica centrada en el origen,
que se mueve alejándose del origen con velocidad