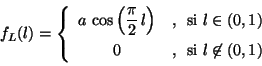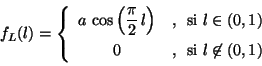Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación
Práctico Especial 2001
Problema de Simulación
Presentaremos un versión simplificada de un problema de
interés en el diseño de bases de datos. A tal fin consideremos
objetos unidimensionales caracterizados por su longitud 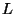 , la cual
es una variable aleatoria continua cuya densidad de probabilidad
está dada por:
, la cual
es una variable aleatoria continua cuya densidad de probabilidad
está dada por:
a) Calcular el valor de la constante 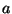 .
.
b) Construir la función de distribución acumulada
de la variable 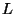 .
.
c) Calcular exactamente ![$E[L]$](img4.gif) y
y ![$\mbox{Var}[L]$](img5.gif) .
.
Se escogen ahora al azar de manera independiente 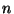 objetos,
cuyas longitudes resultan:
objetos,
cuyas longitudes resultan:
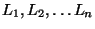 . Estos objetos deben
ser guardados consecutivamente en cajas unidimensionales de
longitud
. Estos objetos deben
ser guardados consecutivamente en cajas unidimensionales de
longitud 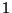 y en el orden de sus correspondientes índices.
Además, ningún objeto puede ser partido en dos cajas.
Esta última condición implica que puede generarse una
gran cantidad de espacio desperdiciado en las cajas utilizadas.
Sea
y en el orden de sus correspondientes índices.
Además, ningún objeto puede ser partido en dos cajas.
Esta última condición implica que puede generarse una
gran cantidad de espacio desperdiciado en las cajas utilizadas.
Sea 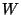 la cantidad de espacio desperdiciado y
la cantidad de espacio desperdiciado y 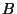 el número de
cajas empleadas para almacenar los
el número de
cajas empleadas para almacenar los 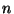 objetos. Obviamente se cumple
que
objetos. Obviamente se cumple
que 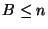 . Para clarificar la notación y las condiciones de
almacenamiento consideremos el siguiente ejemplo:
Supongamos
. Para clarificar la notación y las condiciones de
almacenamiento consideremos el siguiente ejemplo:
Supongamos 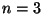 , y
, y 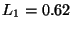 ,
, 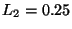 y
y 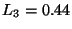 .
Entonces los objetos
.
Entonces los objetos 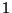 y
y 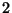 se acomodan en la caja
se acomodan en la caja 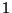 y el
objeto
y el
objeto 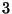 se acomoda en la caja
se acomoda en la caja 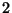 . Se tiene que
. Se tiene que
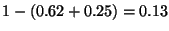 es el espacio vacío en la primer caja
y
es el espacio vacío en la primer caja
y
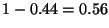 es el espacio desperdiciado en la caja
es el espacio desperdiciado en la caja 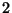 .
Por lo tanto,
.
Por lo tanto,
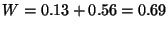 y
y 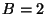 .
.
Con el fin de realizar simulaciones numéricas,
desarrollar un programa que reproduzca el algoritmo de
almacenamiento de los objetos en las cajas.
Probar su funcionamiento reproduciendo el ejemplo anterior.
Desarrollar un generador para la variable aleatoria 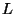 ,
empleando la idea de la transformación integral desarrollada en
la sección 13.5 del libro de
referencia
,
empleando la idea de la transformación integral desarrollada en
la sección 13.5 del libro de
referencia
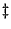 .
.
d) Generar 100000 valores de 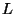 empleando el
generador construído y calcular el promedio y varianza de la
muestra obtenida. Comparar estos resultados con los calculados
en el item (c).
empleando el
generador construído y calcular el promedio y varianza de la
muestra obtenida. Comparar estos resultados con los calculados
en el item (c).
Asumir ahora 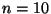 y mediante simulaciones numéricas en la
computadora (utilizar 100000 simulaciones), estimar:
y mediante simulaciones numéricas en la
computadora (utilizar 100000 simulaciones), estimar:
e) el valor medio y la varianza de 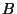
f) 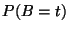 para
para
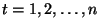 ,
,
g) el valor medio y la varianza de 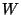 ,
,
h) el valor medio del cociente 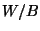 , es decir la
proporción esperada de espacio vacío, y la correspondiente
varianza de esta cantidad.
, es decir la
proporción esperada de espacio vacío, y la correspondiente
varianza de esta cantidad.
Problema de Estadística
Para el estudio del clima y su cambio se requiere de la
acumulación de mediciones de varias magnitudes meteorológicas
durante períodos de tiempo que superen el siglo.
Sobre estas series temporales de mediciones se implementa el
análisis estadístico.
En particular, la estación meteorológica Córdoba funciona de
manera continuada desde el año 1872, siendo una de las primeras en
establecerse en América.
Con el fin de implementar un primer estudio con base estadística
del clima en Córdoba, en el archivo
lluvias.dat
se compilan los registros pluviométricos anuales (en mm)
correspondientes al período 1873-1992. Utilizando la muestra
de valores de lluvia caída en Córdoba:
a) Identificar los valores máximos, mínimos
y la mediana.
b) Calcular la media y la varianza.
c) Confeccionar un histograma de frecuencias
relativas tomando 20 particiones en el intervalo ![$[400,1400]\,$](img27.gif) mm.
mm.
d) Realizar el estudio de cuantiles en la muestra y
confeccionar el correspondiente ``box plot''.
Con el fin de establecer si existe cambio climático se propone:
e) Graficar la lluvia caída (en mm) en función
del tiempo (en años) para el período 1876-1990.
(Excluímos adrede los valores extremos de la muestra para el
subsiguiente análisis).
f) Considerar las submuestras: A correspondiente
al intervalo de años [1876,1935] y B correspondiente
al intervalo de años [1936,1990].
Realizar un ajuste lineal mediante el método de los mínimos
cuadrados (desarrollado en la sección
14.5 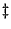 ) de ambas
submuestras. Destacar los valores de las pendientes (
) de ambas
submuestras. Destacar los valores de las pendientes (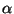 )
obtenidas y sus correspondientes varianzas. Superponer las rectas
calculadas sobre la gráfica del item anterior.
)
obtenidas y sus correspondientes varianzas. Superponer las rectas
calculadas sobre la gráfica del item anterior.
g) Calcular el 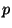 -valor de la prueba de hipótesis:
-valor de la prueba de hipótesis:
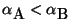 .
.
h) Qué conclusión puede extraerse del análisis
realizado?
Referencia:
 Probabilidad y Aplicaciones Estadísticas.
Paul L. Meyer (Addison Wesley Longman, edición revisada, 1998)
Probabilidad y Aplicaciones Estadísticas.
Paul L. Meyer (Addison Wesley Longman, edición revisada, 1998)
Fa.M.A.F ©2001
Pedro Pury
2001-10-05