Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N 3:
Probabilidad Condicional e Independencia
3:
Probabilidad Condicional e Independencia
Problema 1: Suponga que se tienen 2 urnas, 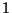 y
y 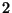 , cada una de ellas
con dos cajones. La urna
, cada una de ellas
con dos cajones. La urna 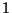 contiene una moneda de oro en un cajón
y una de plata en el otro, mientras que la urna
contiene una moneda de oro en un cajón
y una de plata en el otro, mientras que la urna 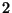 tiene una moneda
de oro en cada uno de los cajones. Se escoge una urna al azar, y de
esta se escoge un cajón al azar. La moneda que se encontró en
este cajón es de oro. ¿Cuál es la probabilidad
que la moneda elegida provenga de la urna
tiene una moneda
de oro en cada uno de los cajones. Se escoge una urna al azar, y de
esta se escoge un cajón al azar. La moneda que se encontró en
este cajón es de oro. ¿Cuál es la probabilidad
que la moneda elegida provenga de la urna 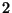 ?
?
Problema 2: Un número binario está compuesto sólo de los
dígitos 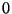 y
y 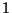 . Suponga que un número binario está
formado por
. Suponga que un número binario está
formado por 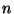 dígitos. Suponga además, que la probabilidad
de que contenga un dígito incorrecto es
dígitos. Suponga además, que la probabilidad
de que contenga un dígito incorrecto es 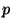 y que los errores
en dígitos diferentes son independientes uno de otro.
¿Cuál es la probabilidad de formar un
número incorrecto?
y que los errores
en dígitos diferentes son independientes uno de otro.
¿Cuál es la probabilidad de formar un
número incorrecto?
Problema 3: Sean A y B dos eventos asociados con un experimento.
Supóngase que 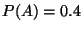 , mientras que
, mientras que
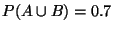 .
Sea
.
Sea 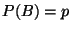 .
.
a) ¿Para qué elección de
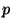 son A y B mutuamente excluyentes?
son A y B mutuamente excluyentes?
b) ¿Para qué elección de
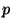 son A y B independientes?
son A y B independientes?
Problema 4: Sean A y B dos eventos independientes. Probar que: A y 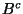 ,
,
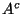 y B, y
y B, y 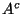 y
y 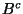 son independientes.
son independientes.
Problema 5: En la fabricación de cierto artículo se presenta un
cierto tipo de defecto con una probabilidad igual a 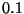 y se
presentan defectos de un segundo tipo con una probabilidad igual
a
y se
presentan defectos de un segundo tipo con una probabilidad igual
a 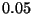 . (Se supone que la ocurrencia de los distintos tipos de
defectos son eventos independientes).
¿Cuál es la probabilidad de que
. (Se supone que la ocurrencia de los distintos tipos de
defectos son eventos independientes).
¿Cuál es la probabilidad de que
a) un artículo no tenga ambas clases de defectos?
b) un artículo sea defectuoso?
c) suponiendo que un artículo sea defectuoso,
tenga un sólo tipo de defecto?
Problema 6: Verificar que el teorema de la multiplicación
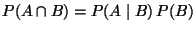 , establecido para dos eventos,
se puede generalizar para tres eventos según:
, establecido para dos eventos,
se puede generalizar para tres eventos según:
Problema 7: Dos tubos defectuosos se confunden con dos buenos.
Los tubos se prueban, uno por uno, hasta encontrar los defectuosos.
a) ¿Cuál es la probabilidad de
encontrar el último tubo defectuoso en la segunda prueba?
b)¿ Cuál es la probabilidad de
encontrar el último tubo defectuoso en la tercera prueba?
c) ¿Cuál es la probabilidad de
encontrar el último tubo defectuoso en la cuarta prueba?
d) Sumar los resultados obtenidos en (a), (b) y (c),
le sorprende el resultado obtenido?
Problema 8: Un aficionado usa el siguiente sistema, bastante simple, para
pronosticar el tiempo atmosférico. Clasifica cada día como
``seco'' o ``mojado'' y supone que la probabilidad de que un día
cualquiera dado sea igual al anterior está dada por una
constante 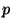 (
(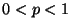 ).
En base a anotaciones anteriores, se asume que el
).
En base a anotaciones anteriores, se asume que el 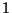 de enero
tiene una probabilidad
de enero
tiene una probabilidad 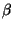 de ser ``seco''.
Suponiendo que
de ser ``seco''.
Suponiendo que 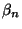 es la probabilidad el
es la probabilidad el 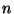 -ésimo día
del año sea ``seco'', obtener una expresión para
-ésimo día
del año sea ``seco'', obtener una expresión para 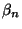 en
función de
en
función de 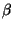 y
y 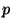 .
.
Ayuda: Observar que
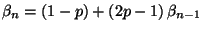 ,
con
,
con 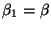 y recordar que
y recordar que
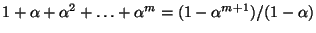 .
.
Evaluar también el límite de 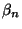 para
para
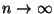 e interpretar el resultado.
e interpretar el resultado.
Problema 9: En un test de múltiples opciones, la probabilidad que un
alumno sepa la respuesta es 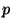 . Teniendo
. Teniendo 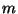 opciones, el estudiante
que sabe la respuesta, responde correctamente con probabilidad
opciones, el estudiante
que sabe la respuesta, responde correctamente con probabilidad 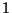 ;
mientras que si no la sabe responde correctamente con probabilidad
;
mientras que si no la sabe responde correctamente con probabilidad
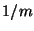 .
¿Cuál es la probabilidad de que el alumno conozca
la respuesta si respondió la pregunta correctamente?
.
¿Cuál es la probabilidad de que el alumno conozca
la respuesta si respondió la pregunta correctamente?
Problema 10: Durante el mes de noviembre la probabilidad de lluvia
es 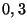 . Cierto equipo de fútbol gana un partido en los días
de lluvia con probabilidad
. Cierto equipo de fútbol gana un partido en los días
de lluvia con probabilidad 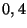 y en un día sin lluvia con
probabilidad
y en un día sin lluvia con
probabilidad 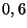 . Si dicho equipo ganó un partido en noviembre,
cuál es la probabilidad que haya llovido
ese día?
. Si dicho equipo ganó un partido en noviembre,
cuál es la probabilidad que haya llovido
ese día?
Problema 11: Suponga que una determinada característica oftálmica
está asociada con el color de ojos. Se estudiaron 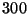 personas,
seleccionadas al azar, y se obtuvieron los siguientes resultados:
personas,
seleccionadas al azar, y se obtuvieron los siguientes resultados:
| |
Color de ojos |
|
| Característica |
Azul |
Café |
Otro |
Totales |
| Si |
70 |
30 |
20 |
120 |
| No |
20 |
110 |
50 |
180 |
| Totales |
90 |
140 |
70 |
300 |
a) ¿Cuál es la probabilidad
de que una persona seleccionada al azar tenga los ojos azules?
b) ¿Cuál es la probabilidad
de que una persona seleccionada al azar posea la característica
oftálmica?
c) ¿Son independientes los
eventos 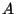 (tener ojos azules) y
(tener ojos azules) y 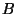 (poseer la característica)?
Justificar la respuesta.
(poseer la característica)?
Justificar la respuesta.
d) ¿Qué relación se establece
entre los eventos 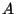 (tener ojos azules) y
(tener ojos azules) y 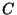 (tener ojos café)?
¿Son independientes, mutuamente excluyentes,
complementarios?
Explicar si se aplica o no cada una de estas categorías.
(tener ojos café)?
¿Son independientes, mutuamente excluyentes,
complementarios?
Explicar si se aplica o no cada una de estas categorías.
Problema 12: Un test de sangre es efectivo para detectar el SIDA, cuando
la enfermedad está presente en los pacientes analizados, el 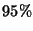 de las veces. Sin embargo el test produce un resultado falso positivo
el
de las veces. Sin embargo el test produce un resultado falso positivo
el 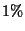 de las veces. Suponga que el
de las veces. Suponga que el 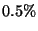 de una población
padece la enfermedad. ¿Cuál es la probabilidad
que una persona se encuentre enferma de SIDA si el test arrojó
un resultado positivo?
de una población
padece la enfermedad. ¿Cuál es la probabilidad
que una persona se encuentre enferma de SIDA si el test arrojó
un resultado positivo?
Problema 13: Supongase que una moneda honesta es arrojada tres veces
registrándose el resultado obtenido después de cada una de ellas.
Sea 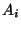 el evento "i-ésima tirada resultó cara", con
el evento "i-ésima tirada resultó cara", con 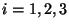 .
Los eventos
.
Los eventos 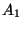 ,
, 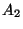 y
y 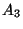 son mutuamente
independientes?
son mutuamente
independientes?
Problema 14: Un conjunto electrónico consta de dos subsistemas,
digamos A y B. A partir de una serie de pruebas previas,
se presuponen las siguientes probabilidades:
| P(A falle) |
= |
0.20 |
| P(sólo falle B) |
= |
0.15 |
| P(A y B fallen) |
= |
0.15 |
a) Calcular las siguientes probabilidades:
i) P(sólo falle A)
ii) que al menos un subsistema falle.
iii) P(A falle 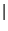 B falló)
B falló)
b) ¿Son A y B eventos independientes?
Fa.M.A.F ©2002
Pedro Pury
2002-08-20