Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N 4:
Variables Aleatorias Unidimensionales
4:
Variables Aleatorias Unidimensionales
Problema 1: Sea X una variable aleatoria con distribución de
probabilidad dada por
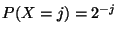
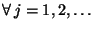 .
Calcular:
.
Calcular:
a)
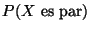
b) 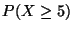
c)
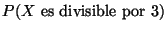
Problema 2: De un lote que contiene 25 artículos, 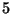 de los cuales
son defectuosos, se eligen
de los cuales
son defectuosos, se eligen 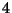 al azar. Sea
al azar. Sea 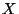 el número de
artículos defectuosos encontrados. Obtener la distribución de
la variable aleatoria
el número de
artículos defectuosos encontrados. Obtener la distribución de
la variable aleatoria 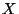 si:
a) los artículos se escogen con sustitución,
b) los artículos se escogen sin sustitución.
si:
a) los artículos se escogen con sustitución,
b) los artículos se escogen sin sustitución.
Problema 3: Se sabe que al lanzar una moneda, la cara sale tres
veces más que el sello. Esta moneda se lanza tres veces.
Sea X el número de caras que aparecen. Establecer la distribución
de probabilidad y la función de distribución acumulativa de X.
Graficarlas.
Problema 4: De los donantes voluntarios de sangre de un hospital,
el  tiene el factor Rh (Rhesus) en su sangre.
tiene el factor Rh (Rhesus) en su sangre.
a) Si se eligen cinco donantes al azar,
¿Cuál es la probabilidad de que al menos uno
no posea el factor Rh?
b) Si se seleccionan cinco voluntarios al azar,
¿Cuál es la probabilidad de que a lo más
cuatro tengan el factor Rh?
c) ¿Cuál será el mínimo
número de donantes que se tienen que convocar, si se desea tener
una seguridad no menor que el 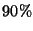 de obtener por lo menos cinco
donantes con el factor Rh?
de obtener por lo menos cinco
donantes con el factor Rh?
Problema 5: Se lanzan una serie de cohetes hasta que ocurre el
primer lanzamiento exitoso. Si esto no sucede en cinco ensayos,
el experimento se detiene y se inspecciona el equipo. Suponer que
hay una probabilidad constante igual a 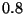 de tener un lanzamiento
exitoso y que los ensayos sucesivos son independientes.
Además el costo del primer lanzamiento es de
de tener un lanzamiento
exitoso y que los ensayos sucesivos son independientes.
Además el costo del primer lanzamiento es de 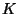 dólares,
mientras que los siguientes cuestan
dólares,
mientras que los siguientes cuestan 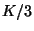 dólares. Cada vez que
hay un lanzamiento exitoso, se obtiene cierta cantidad de
información que puede expresarse como una ganancia financiera
igual a
dólares. Cada vez que
hay un lanzamiento exitoso, se obtiene cierta cantidad de
información que puede expresarse como una ganancia financiera
igual a 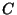 dólares. Si
dólares. Si 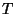 es el costo neto del experimento,
encontrar la distribución de probabilidad de T.
es el costo neto del experimento,
encontrar la distribución de probabilidad de T.
Problema 6: Sea 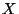 una variable aleatoria continua cuya función
densidad de probabilidades
una variable aleatoria continua cuya función
densidad de probabilidades 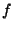 está dada por:
está dada por:
a) Determinar la constante 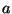 .
.
b) Determinar la función distribución
acumulada 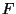 y representarla gráficamente.
y representarla gráficamente.
c) Si 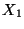 ,
, 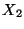 ,
, 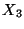 son tres observaciones
independientes de
son tres observaciones
independientes de 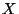 .¿ Cuál es la probabilidad
de que exactamente uno de esos tres números sea mayor que
.¿ Cuál es la probabilidad
de que exactamente uno de esos tres números sea mayor que 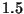 ?
?
Problema 7: La función 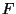 representa la función distribución
acumulada de una variable aleatoria continua. Sabiendo que:
representa la función distribución
acumulada de una variable aleatoria continua. Sabiendo que:
determinar la función densidad de probabilidad 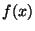 y
graficarla. Verificar que
y
graficarla. Verificar que 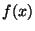 es una función densidad
de probabilidad.
es una función densidad
de probabilidad.
Problema 8: Suponer que la gráfica de la figura representa la
función densidad de la variable aleatoria X.
a) ¿Cuál es la relación entre
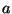 y
y 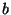 ?
?
b) Si 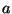 y
y 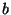 son positivos, qué puede decirse
sobre el máximo valor que puede tomar
son positivos, qué puede decirse
sobre el máximo valor que puede tomar 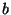 ?
?
Problema 9: Suponga que la variable aleatoria 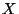 está distribuída
uniformemente en el intervalo
está distribuída
uniformemente en el intervalo
![$[-\alpha,+\alpha]$](img29.gif) , donde
, donde 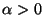 .
Cada vez que sea posible, determinar
.
Cada vez que sea posible, determinar 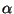 de modo que se
satisfaga la siguiente condición:
de modo que se
satisfaga la siguiente condición:
a)
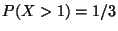 ,
,
b)
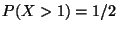 ,
,
c)
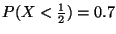 ,
,
d)
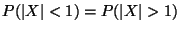 .
.
Problema 10: El porcentaje de alcohol 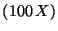 en cierto compuesto se
puede considerar como una variable, donde
en cierto compuesto se
puede considerar como una variable, donde 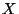 tiene la siguiente
función densidad:
tiene la siguiente
función densidad:
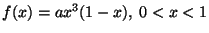 .
.
a) Determinar el valor de la constante 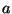 .
.
b) Obtener una expresión para la función de
distribución acumulada, 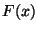 , y graficarla.
, y graficarla.
c) Calcular 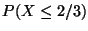 .
.
d) Suponer que el precio de venta del compuesto
anterior depende del contenido de alcohol. Específicamente,
si 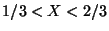 , el compuesto se vende en
, el compuesto se vende en 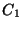 dólares por
galón; de otro modo se vende en
dólares por
galón; de otro modo se vende en 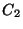 dólares por galón.
Si el costo es de
dólares por galón.
Si el costo es de 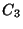 dólares por galón, encontrar la
distribución de probabilidad de la utilidad neta por galón.
dólares por galón, encontrar la
distribución de probabilidad de la utilidad neta por galón.
Problema 11: Si la variable aleatoria 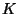 está distribuída
uniformemente en el intervalo
está distribuída
uniformemente en el intervalo ![$[0,5]$](img44.gif) . ¿Cuál es la probabilidad de
que las raíces de la ecuación
. ¿Cuál es la probabilidad de
que las raíces de la ecuación
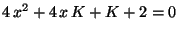 sean reales?
sean reales?
Problema 12: Suponer que la duración (en horas)
de un cierto tubo de radio es una variable aleatoria continua
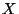 , cuya función densidad es
, cuya función densidad es
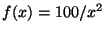 si
si 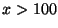 y
y
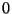 para cualquier otro valor.
para cualquier otro valor.
a) ¿Cuál es al probabilidad de
que el tubo dure menos de 200 hs, si se sabe que el tubo todavía
funciona después de 150 hs de servicio?
b) ¿Cuál es la probabilidad de
que si se instalan tres de estos tubos en un conjunto, exactamente
uno tenga que ser sustituído después de 150 hs de servicio?
c) ¿Cuál es el número máximo
de tubos que se pueden poner en un conjunto de modo tal que haya
una probabilidad de 0.5 de que después de 150 hs de servicio
funcionen todavía?
Problema 13: Suponga que la vida útil de un cierto tipo de lámparas
tiene una distribución exponencial de parámetro 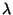 ,
es decir, su función densidad de probabilidad está dada por
,
es decir, su función densidad de probabilidad está dada por
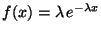 , para
, para 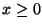 .
.
a) Sea 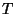 la vida de una lámpara de este tipo.
Mostrar que:
la vida de una lámpara de este tipo.
Mostrar que:
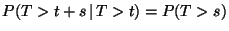
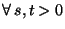 .
.
b) Demuestre que
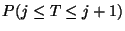 es de la
forma
es de la
forma 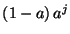 y determine
y determine 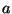 .
.
c) Suponga que 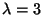 cuando se expresa la vida
útil en días. Una lámpara se enciende en una habitación en
un instante
cuando se expresa la vida
útil en días. Una lámpara se enciende en una habitación en
un instante 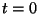 . Un día después usted entra a la habitación
y se queda allí durante 8 horas, saliendo al final de ese
período.
. Un día después usted entra a la habitación
y se queda allí durante 8 horas, saliendo al final de ese
período.
i) ¿Cuál es la probabilidad de que
usted entre a la habitación cuando esta ya está oscura?
ii)¿ Cuál es la probabilidad de que
cuando usted entre a la habitación la lámpara esté encendida
y que se apague mientras usted permace allí?
Fa.M.A.F ©2002
Pedro Pury
2002-08-29
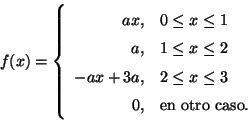
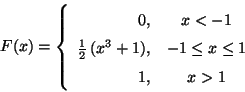
![\begin{picture}(30,30)(15,-20)
\put(0,-16){\vector(1,0){60}}
\put(24,-22){\vec...
...18){\makebox(0,0)[lb]{$x$}}
\put(19,5){\makebox(0,0)[lb]{$f(x)$}}
\end{picture}](img28.gif)