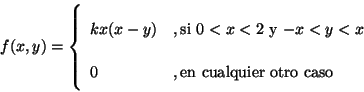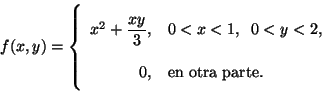Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N 5:
Funciones de Variables Aleatorias y Variables Bidimensionales
5:
Funciones de Variables Aleatorias y Variables Bidimensionales
Problema 1: Suponga que la variable aleatoria discreta 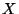 toma los
valores
toma los
valores 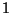 ,
, 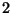 y
y 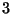 con igual probabilidad.
Calcular la distribución de probabilidad de la variable
aleatoria
con igual probabilidad.
Calcular la distribución de probabilidad de la variable
aleatoria 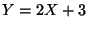 .
.
Problema 2: Una variable aleatoria 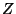 tiene distribución normal
estándar (que denotaremos por
tiene distribución normal
estándar (que denotaremos por
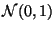 ). La función
densidad de probabilidad esta dada por:
). La función
densidad de probabilidad esta dada por:
a) Obtener la función densidad de 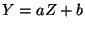 ,
donde
,
donde 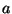 y
y 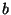 son números reales (
son números reales (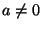 ).
).
b) Obtener la función densidad de 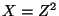 .
.
c) Obtener la función densidad de 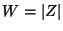 .
.
Problema 3: Sea U una variable aleatoria con distribución
uniforme en el intervalo 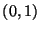 (
(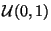 ) y
sea
) y
sea
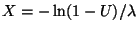 , con
, con 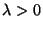 fijo.
fijo.
a) Obtener la función densidad de X.
b) Suponiendo que 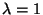 , calcular la
función densidad de probabilidad de las siguientes
variables aleatorias:
, calcular la
función densidad de probabilidad de las siguientes
variables aleatorias:
i) 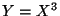 ,
ii)
,
ii)
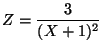 .
.
Problema 4: Suponga que la variable aleatoria 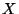 está distribuída
uniformemente en el intervalo
está distribuída
uniformemente en el intervalo 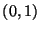 . Calcular la función
densidad de probabilidad de las siguientes variables aleatorias:
. Calcular la función
densidad de probabilidad de las siguientes variables aleatorias:
a) 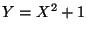 ,
b)
,
b)
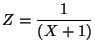 ,
c)
,
c) 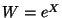 .
.
Problema 5: En la siguiente tabla se representa la distribución de
probabilidad conjunta correspondiente a las variables aleatorias 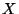 e
e 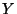 . Calcular las probabilidades marginales
. Calcular las probabilidades marginales 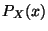 y
y 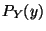 y
las probabilidades condicionales
y
las probabilidades condicionales
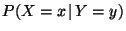 y
y
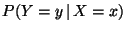 .
.
Problema 6: Cierto supermercado tiene una caja rápida y una común.
Sea 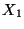 el número de clientes que están en espera en la caja
común en un momento particular del día, y
el número de clientes que están en espera en la caja
común en un momento particular del día, y 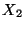 el número
de clientes que están en espera en la caja rápida al mismo
tiempo. Si la densidad conjunta de
el número
de clientes que están en espera en la caja rápida al mismo
tiempo. Si la densidad conjunta de 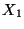 y
y 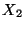 está dada por:
está dada por:
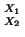 |
0 |
1 |
2 |
3 |
| 0 |
0.08 |
0.07 |
0.04 |
0.00 |
| 1 |
0.06 |
0.15 |
0.05 |
0.04 |
| 2 |
0.05 |
0.04 |
0.10 |
0.06 |
| 3 |
0.00 |
0.03 |
0.04 |
0.07 |
| 4 |
0.00 |
0.01 |
0.05 |
0.06 |
a) ¿Cuál es la probabilidad de que haya exactamente
un cliente en cada caja?
b) ¿Cuál es la probabilidad de que haya exactamente
el mismo número de clientes en las dos líneas de espera?
c) Sea A el evento de que haya por lo menos dos
clientes más en una línea de espera que en la otra.
¿Cuál es la probabilidad del evento A?
d) ¿Cuál es la probabilidad de que el número
total de clientes de las dos líneas de espera sea exactamente
cuatro? ¿Y por lo menos cuatro?
e) Hallar las marginales de 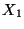 y
y 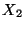 .
¿Son estas variables independientes?
.
¿Son estas variables independientes?
Problema 7: Se asignan aleatoriamente los contratos para dos
construcciones, los cuales pueden ser adjudicados a las empresas 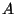 ,
,
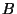 o
o 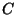 . De esta forma cada empresa puede recibir
. De esta forma cada empresa puede recibir 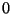 ,
, 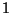 o
o 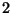 contratos. Sea
contratos. Sea 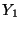 el número de contratos asignados a la empresa
el número de contratos asignados a la empresa
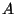 , e
, e 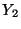 el número de contratos asignados a la empresa
el número de contratos asignados a la empresa 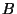 .
.
a) Determinar la función distribución de
probabilidad conjunta para las variables aleatorias 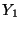 e
e 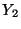 .
.
b) Determinar las probabilidades marginales de las
variables 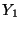 e
e 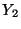 .
.
c) ¿Son independientes 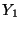 e
e 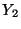 ?
Justificar.
?
Justificar.
Problema 8: Suponga que se sacan dos cartas al azar de una baraja.
Sea 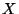 el número de ases obtenidos e
el número de ases obtenidos e 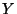 el número de reinas
obtenido. Teniendo en cuenta que la baraja posee
el número de reinas
obtenido. Teniendo en cuenta que la baraja posee 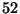 cartas, siendo
cuatro los ases y cuatro las reinas,
cartas, siendo
cuatro los ases y cuatro las reinas,
a) Obtener la distribución de probabilidad
conjunta de 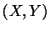 .
.
b) Obtener la distribución marginal de 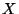 y de
y de 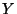 .
.
c) Obtener la distribución condicional de 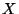 dado
dado 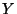 y de
y de 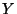 dado
dado 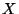 .
.
Problema 9: Sea 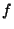 la función densidad del vector aleatorio
la función densidad del vector aleatorio 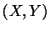 dada por:
dada por:
a) Determine el valor de la constante 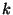 .
.
b) Hallar las marginales de X e Y.
Problema 10: Suponga que la función densidad de probabilidad conjunta de
la variable aleatoria bidimensional 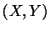 está dada por:
está dada por:
a) Encontrar las densidades de probabilidad marginales
de 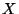 e
e 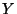
b) Calcular:
i) 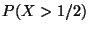 ,
ii)
,
ii) 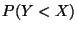 ,
iii)
,
iii)
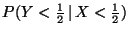 .
.
Problema 11: Se selecciona al azar un punto en el cuadrado unitario
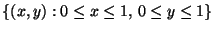 . Sean
. Sean 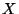 e
e 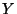 las
coordenadas del punto seleccionado.
las
coordenadas del punto seleccionado.
a) ¿Cuál es la densidad conjunta de 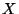 e
e 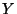 ?
?
b) Calcular las densidades marginales de 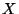 e
e 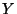 .
.
c) Calcular
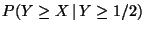 .
.
Problema 12: Sean 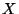 e
e 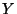 variables aleatorias independientes
idénticamente distribuídas con una distribución uniforme en
el intervalo
variables aleatorias independientes
idénticamente distribuídas con una distribución uniforme en
el intervalo 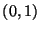 . Encontrar la densidad conjunta de
. Encontrar la densidad conjunta de 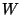 y
y 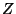 ,
donde
,
donde 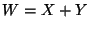 y
y 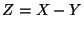 . ¿Son
. ¿Son 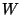 y
y 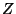 independientes?
independientes?
Fa.M.A.F ©2002
Pedro Pury
2002-09-18