Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N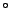 7: Distribuciones Muestrales
7: Distribuciones Muestrales
Problema 1: La variable aleatoria 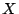 que toma valores en los enteros no
negativos tiene una distribución de Poisson con parámetro
que toma valores en los enteros no
negativos tiene una distribución de Poisson con parámetro
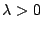 si:
si:
a) Calcular la media y la varianza de 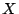 .
.
Sean 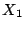 y
y 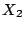 dos variables aleatorias independientes
con distribuciones de Poisson de parámetros
dos variables aleatorias independientes
con distribuciones de Poisson de parámetros 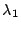 y
y
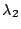 , respectivamente.
, respectivamente.
b) Calcular la distribución de probabilidad
de la variable 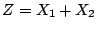 .
.
Problema 2: Sean 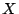 e
e 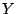 variables aleatorias independientes, distribuídas
con densidad de probabilidad exponencial de parámetros
variables aleatorias independientes, distribuídas
con densidad de probabilidad exponencial de parámetros 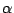 y
y 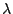 , respectivamente. Calcular la densidad de la variable
, respectivamente. Calcular la densidad de la variable
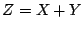 .
.
Problema 3: Sea
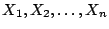 una muestra aleatoria
con distribución de probabilidad acumulada
una muestra aleatoria
con distribución de probabilidad acumulada 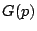 .
Sean
.
Sean
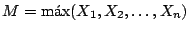 y
y
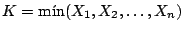 .
Calcular las ditribuciones de
.
Calcular las ditribuciones de 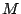 y
y 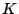 .
.
Problema 4: Considerar que 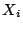 ,
,
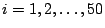 son variables
aleatorias independientes e idénticamente distribuídas con
una distribución de Poisson con parámetro
son variables
aleatorias independientes e idénticamente distribuídas con
una distribución de Poisson con parámetro
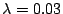 .
Sea
.
Sea
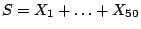 .
.
Calcular 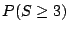 :
:
a) exactamente, usando la distribución
de probabilidad de 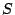 .
.
b) de forma aproximada usando
el teorema central del límite.
Problema 5: Sean 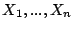 variables aleatorias independientes,
cada una de las cuales con distribución exponencial
con parámetro
variables aleatorias independientes,
cada una de las cuales con distribución exponencial
con parámetro 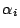 ,
,
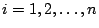 y sea
y sea
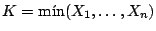 .
.
a) Probar que 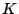 tiene una distribución
exponencial con parámetro
tiene una distribución
exponencial con parámetro
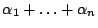 .
.
b) Si
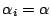 ,
,
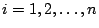 ; calcular
; calcular 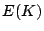 .
.
Problema 6: Sean 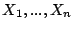 son variables aleatorias
independientes e idénticamente distribuídas de forma
uniforme:
son variables aleatorias
independientes e idénticamente distribuídas de forma
uniforme:
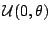 y sea
y sea
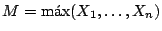 .
Calcular la distribución de probabilidad de
.
Calcular la distribución de probabilidad de 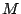 y
y 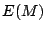 .
.
Problema 7: Se obtiene una muestra de tamaño 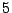 de una variable
aleatoria con distribución
de una variable
aleatoria con distribución 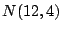 :
:
a) ¿Cuál es la probabilidad de que el promedio
muestral exceda 13?
b) ¿Cuál es la probabilidad de que el mínimo
de la muestra sea menor que 10?
c) ¿Cuál es la probabilidad de que el máximo de
la muestra exceda 15?
Problema 8: La duración de un artículo (expresada en horas) está
distribuída exponencialmente con parámetro 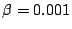 . Se
prueban seis artículos y se anotan los tiempos en que ocurren
las fallas.
. Se
prueban seis artículos y se anotan los tiempos en que ocurren
las fallas.
a) ¿Cuál es la probabilidad de que ningún
artículo falle antes de que hayan transcurrido 800 horas?
b) ¿Cuál es la probabilidad de que ningún
artículo dure más de 3000 horas?
Problema 9: La variable aleatoria continua 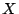 está distríbuida
uniformemente en el intervalo
está distríbuida
uniformemente en el intervalo
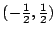 .
.
Se obtiene una muestra de tamaño 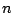 de
de 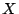 y se calcula el
promedio muestral
y se calcula el
promedio muestral 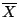 .
¿Cuál es la desviación estándar de
.
¿Cuál es la desviación estándar de 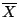 ?
?
Problema 10: Se toman dos muestras de tamaño 10 y 15 de una variable
aleatoria normal con media 20 y varianza 3.
¿Cuál es la probabilidad de que el promedio de las dos muestras
se diferencie (en valor absoluto) en más de 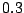 ?
?
Problema 11: La variable aleatoria 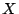 tiene distribución
tiene distribución 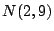 .
Sean
.
Sean
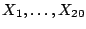 una muestra aleatoria de
una muestra aleatoria de 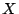 obtenida
con la ayuda de la Tabla 7 del Apéndice del libro
Probabilidad y Aplicaciones Estadísticas de Paul Meyer.
Calcular la varianza muestral:
obtenida
con la ayuda de la Tabla 7 del Apéndice del libro
Probabilidad y Aplicaciones Estadísticas de Paul Meyer.
Calcular la varianza muestral:
donde 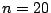 y comparar el resultado numérico obtenido con el
valor teórico
y comparar el resultado numérico obtenido con el
valor teórico 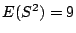 .
.
Fa.M.A.F ©2002
Pedro Pury
2002-10-08