Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Práctico Especial 2002: Soluciones
Problema de Probabilidad
a)
b)
c)
Problema de Estadística
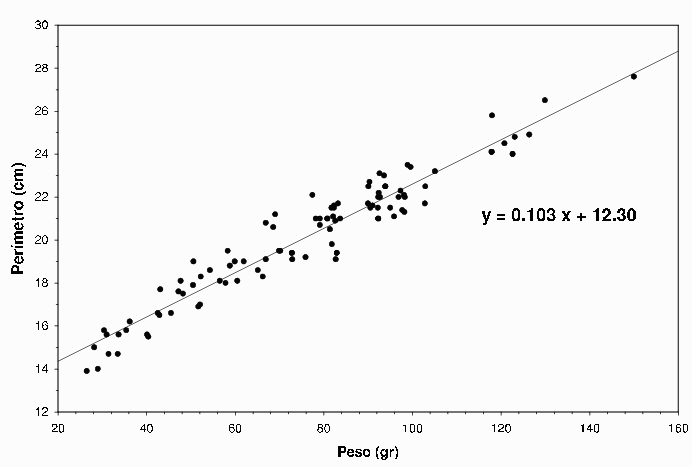
a-b) Ajuste lineal:
c-d) Estadística de los residuos:
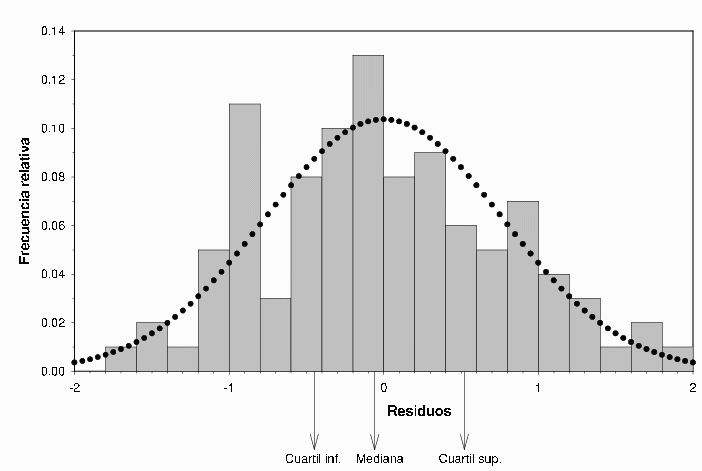
e) Histograma de los residuos y comparación
con la normal:
g) Prueba de hipótesis sobre los residuos:
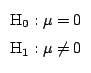
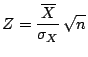
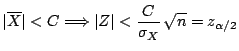
Aproximando
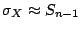 tenemos que:
tenemos que:
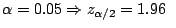 y
y
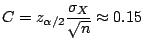
Resulta así que se cumple la condición
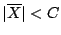 y por lo tanto la muestra no aporta evidencia
suficiente para rechazar H
y por lo tanto la muestra no aporta evidencia
suficiente para rechazar H .
.
h) Prueba de hipótesis sobre los parámetros
del ajuste lineal:
h1)
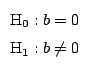
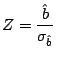
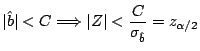
El p-valor es el menor valor de 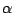 que admite
la muestra para rechazar, y corresponde a
que admite
la muestra para rechazar, y corresponde a 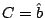 .
Por lo tanto:
.
Por lo tanto:
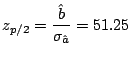 y resulta
y resulta 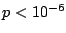 .
.
h2)
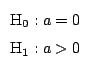
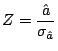
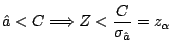
El p-valor es el menor valor de 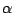 que admite
la muestra para rechazar, y corresponde a
que admite
la muestra para rechazar, y corresponde a 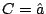 .
Por lo tanto:
.
Por lo tanto:
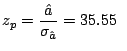 y resulta
y resulta 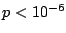 .
.
Fa.M.A.F ©2002
Pedro Pury
2002-11-12
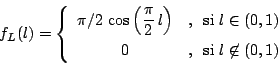
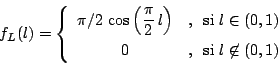
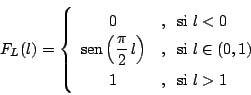
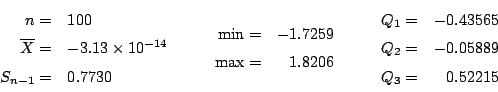
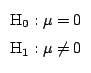
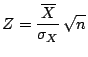
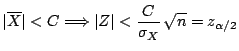
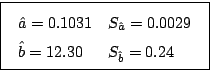
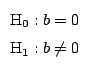
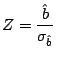
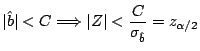
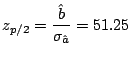 y resulta
y resulta 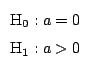
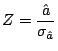
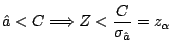
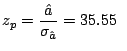 y resulta
y resulta