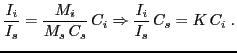Siguiente: Adición de estándares
Subir: Métodos alternativos
Anterior: Métodos alternativos
En este método se agrega un elemento 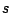 en una proporción conocida tanto
a las muestras incógnitas como a los estándares. La idea central es que
para el ``estándar interno''
en una proporción conocida tanto
a las muestras incógnitas como a los estándares. La idea central es que
para el ``estándar interno'' 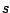 , los efectos de matriz sean similares a
los correspondientes al analito
, los efectos de matriz sean similares a
los correspondientes al analito 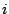 --por supuesto, no siempre es posible
lograr este objetivo. Si esto ocurre, podemos sintetizar las relaciones
entre
--por supuesto, no siempre es posible
lograr este objetivo. Si esto ocurre, podemos sintetizar las relaciones
entre 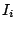 e
e 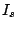 como
como
donde 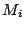 y
y 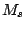 representan las correspondientes correcciones por
efecto de matriz. Si bien
representan las correspondientes correcciones por
efecto de matriz. Si bien 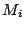 y
y 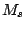 no son iguales, al variar
levemente la composición de la muestra, la razón
no son iguales, al variar
levemente la composición de la muestra, la razón 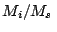 se mantendrá
constante, de modo que
se mantendrá
constante, de modo que
La constante 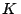 puede determinarse mediante una regresión lineal sobre
las muestras patrones, y luego la concentración de
puede determinarse mediante una regresión lineal sobre
las muestras patrones, y luego la concentración de 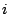 en las muestras se
determina directamente.
en las muestras se
determina directamente.
Gustavo Castellano 15/05/2009
![]() en una proporción conocida tanto
a las muestras incógnitas como a los estándares. La idea central es que
para el ``estándar interno''
en una proporción conocida tanto
a las muestras incógnitas como a los estándares. La idea central es que
para el ``estándar interno'' ![]() , los efectos de matriz sean similares a
los correspondientes al analito
, los efectos de matriz sean similares a
los correspondientes al analito ![]() --por supuesto, no siempre es posible
lograr este objetivo. Si esto ocurre, podemos sintetizar las relaciones
entre
--por supuesto, no siempre es posible
lograr este objetivo. Si esto ocurre, podemos sintetizar las relaciones
entre ![]() e
e ![]() como
como