Siguiente: Eficiencia de un detector Subir: Espectrómetros dispersivos en energías Anterior: Espectrómetros dispersivos en energías

Resolución en energía

Si la energía media para la creación de un par electrón-hueco es $\epsilon$ (=3,8eV), el número de pares electrón-hueco generado en la detección de un fotón con energía $E$ es en realidad una variable aleatoria cuyo valor medio es $E/\epsilon$ . Ya hemos dicho que idealmente una variable estocástica así definida estaría afectada por una desviación cuadrática media $\sigma_s$ debida a la estadística $\sqrt{E/\epsilon}$ ; sin embargo esta aproximación se debe corregir introduciendo el factor de Fano $F$ pues la producción de pares electrón-hueco no es completamente aleatoria:

$$\sigma_s = \sqrt{\frac{F E}{\epsilon}} \;.$$

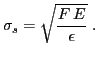
El error cuadrático medio para la energía se obtiene multiplicando este error por $\epsilon$ ; sin embargo, la incertidumbre en la energía $\Delta E_s$ suele caracterizarse mediante el $FWHM$ (full width at half maximum: ancho total a la mitad del máximo)

$$\Delta E_s \equiv FWHM_s = 2,355 \sigma_s = 2,355 \sqrt{F E \epsilon}\;.$$

Por supuesto, a esta incertidumbre debe agregarse la contribución del ruido electrónico $\Delta E_n$ , de modo que

$$\Delta E ^2 = \Delta E_s ^2 + \Delta E_n ^2 \;.$$

Por convención, la resolución de un detector se especifica para la línea K$\alpha$ del manganeso (5,9keV). Un valor razonable para un detector de silicio es $\simeq$ 170eV; los detectores más modernos pueden alcanzar un valor $\simeq$ 130eV, que resulta muy bueno frente a lo que se lograba con detectores convencionales. En el caso de tratarse de HPGe, la resolución resulta $\simeq$ 115eV.

Siguiente: Eficiencia de un detector Subir: Espectrómetros dispersivos en energías Anterior: Espectrómetros dispersivos en energías