Tight binding: sólido iónico unidimensional
En este ejemplo imaginamos una cadena unidimensional en la que se alternan iones $A$ con iones $B$, diferentes, y en los estados electrónicos resultantes solo un orbital asociado a los átomos aislados. Suponemos que los iones $A$ son los cationes y los $B$ los aniones, es decir, las autoenergías asociada a los átomos aislados cumplen $\varepsilon_A>\varepsilon_B$. Estos iones están ordenados regularmente, separados unos de otros una distancia $d$, de manera que el parámetro de red es $a=2d$.
En la construcción de nuestra base que respeta el teorema de Bloch deben intervenir tanto los orbitales $\phi_A$ como los $\phi_B$
\[ \chi_{{}\displaystyle_{k}} = \frac{1}{\sqrt{N}} \sum_m e^{ikma} \left[ \alpha_k\, \phi_A\big(x-ma\big) + \beta_k\, \phi_B\big(x-(ma+d)\big) \right] = \alpha_k\, \chi_{{}\displaystyle_{k}}^A + \beta_k\, \chi_{{}\displaystyle_{k}}^B \;. \]
Aquí conviene resaltar que como no hay solapamiento entre orbitales de iones vecinos
\[ \big\langle \phi_A\big(x-ma\big)\,\big|\, \phi_B\big(x-(ma+d)\big) \big\rangle = 0 \qquad \Rightarrow\qquad \big\langle \chi_{{}\displaystyle_{k}}^A\,\big|\, \chi_{{}\displaystyle_{k}}^B \big\rangle = 0 \; \qquad \Big( \big\langle \chi_{{}\displaystyle_{k}}^A\,\big|\, \chi_{{}\displaystyle_{k}}^A \big\rangle = \big\langle \chi_{{}\displaystyle_{k}}^B\,\big|\, \chi_{{}\displaystyle_{k}}^B \big\rangle = 1 \Big) \]
Las autofunciones $\psi_{nk}$ del hamiltoniano del sistema se conforman como
\[ \require{color} \psi_{nk}(x) = \textcolor{GreenYellow}{\sum_\lambda} \chi_{{}\displaystyle_{k\color{GreenYellow}\lambda}}(x) = \alpha_k\, \chi_{{}\displaystyle_{k}}^A + \beta_k\, \chi_{{}\displaystyle_{k}}^B \;, \]
donde habrá que sumar sobre los diferentes orbitales que intervengan en el caso en que sea necesario considerar más de uno —no en nuestro caso. Los elementos de matriz del hamiltoniano resultan
\[ \big\langle \chi_{{}\displaystyle_{k}}^A \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^B \big\rangle = \frac{1}{N} \sum_{m,m'} e^{ik(m'-m)a} \, \big\langle \phi_A\big(x-ma\big) \big| \hat{H} \big| \phi_B\big(x-(m'a+d)\big) \big\rangle \;. \]
En la matriz del hamiltoniano, los elementos no nulos son únicamente los que involucran dos iones contiguos (siempre $A$ y $B$)
\[ \big\langle \phi_A\big(x-ma\big) \big| \hat{H} \big| \phi_B\big(x-(ma+d)\big) \big\rangle = \big\langle \phi_A\big(x-ma\big) \big| \hat{H} \big| \phi_B\big(x-((m\!-\!1)a+d)\big) \big\rangle = \gamma \;, \]
de manera que
\[ \big\langle \chi_{{}\displaystyle_{k}}^A \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^B \big\rangle = \frac{1}{N} \sum_{m,m'} e^{ik(m'-m)a} \, \gamma \left(\delta_{m',m}+\delta_{m',m-1}\right) = \gamma \left( 1+e^{-ika} \right) = \big\langle \chi_{{}\displaystyle_{k}}^B \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^A \big\rangle^* \;. \]
Vale la pena aclarar que, a diferencia de muchos textos (entre ellos el Aschroft), en nuestra construcción aproximamos
\[ \big\langle \phi_{A,B}(x-ma) \big| \hat{H} \big| \phi_{A,B}(x-ma) \big\rangle = \varepsilon_{A,B} \;, \]
lo que equivale a plantear que en las inmediaciones de los iones, donde las $\phi\neq0$, solo es importante el hamiltoniano de átomos aislados (sin campo cristalino), es decir
\[ \big\langle \phi_{A,B}(x-ma) \big| (\hat{H}-\hat{H}_o) \big| \phi_{A,B}(x-ma) \big\rangle \simeq 0 \;. \]
Entonces estamos en condiciones de proyectar la ecuación de autovalores
\[ \hat{H}\psi_{nk}(x) = \alpha_k\,\hat{H}\chi_{{}\displaystyle_{k}}^A(x) + \beta_k\,\hat{H}\chi_{{}\displaystyle_{k}}^B(x) = \varepsilon(k)\, \psi_{nk}(x) \]
sobre los elementos de la base $\left\{\chi_{{}\displaystyle_{k}}^A,\chi_{{}\displaystyle_{k}}^B\right\}$ : \begin{align*} \big\langle \chi_{{}\displaystyle_{k}}^A \big| \hat{H} \big| \psi_{nk} \big\rangle = \alpha_k\, \big\langle \chi_{{}\displaystyle_{k}}^A \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^A \big\rangle + \beta_k\, \big\langle \chi_{{}\displaystyle_{k}}^A \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^B \big\rangle = \varepsilon(k)\, \Big( \alpha_k &\,\big\langle \chi_{{}\displaystyle_{k}}^A\,\big|\, \chi_{{}\displaystyle_{k}}^A \big\rangle + \beta_k\,\big\langle \chi_{{}\displaystyle_{k}}^A\,\big|\, \chi_{{}\displaystyle_{k}}^B \big\rangle \Big) \\ & \Rightarrow\quad \alpha_k\,\varepsilon_A + \beta_k\,\gamma \left(1+e^{-ika}\right) = \alpha_k\,\varepsilon(k) \\ & \\ \big\langle \chi_{{}\displaystyle_{k}}^B \big| \hat{H} \big| \psi_{nk} \big\rangle = \alpha_k\, \big\langle \chi_{{}\displaystyle_{k}}^B \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^A \big\rangle + \beta_k\, \big\langle \chi_{{}\displaystyle_{k}}^B \big| \hat{H} \big| \chi_{{}\displaystyle_{k}}^B \big\rangle = \varepsilon(k)\, \Big( \alpha_k &\,\big\langle \chi_{{}\displaystyle_{k}}^B\,\big|\, \chi_{{}\displaystyle_{k}}^A \big\rangle + \beta_k\,\big\langle \chi_{{}\displaystyle_{k}}^B\,\big|\, \chi_{{}\displaystyle_{k}}^B \big\rangle \Big) \\ & \Rightarrow\qquad \alpha_k\,\gamma \left(1+e^{ika}\right) + \beta_k\,\varepsilon_B = \beta_k\,\varepsilon(k) \;, \end{align*}
que conforma un sistema de ecuaciones para los coeficientes $\alpha_k$ y $\beta_k$
\[ \left( \begin{array}{cc} \varepsilon_A-\varepsilon(k) & \gamma \left(1+e^{-ika}\right) \\ & \\ \gamma \left(1+e^{ika}\right) & \varepsilon_B-\varepsilon(k) \end{array} \right) \left( \begin{array}{c} \alpha_k \\ \\ \beta_k \end{array} \right) = 0 \;. \]
Este sistema puede construirse directamente al comenzar el planteo de la ecuación de autovalores
\[ \sum_j \left[ \big\langle\chi_{{}\displaystyle_{\boldsymbol{k}\ell}}\big| \hat{H} \big|\chi_{{}\displaystyle_{\boldsymbol{k}j}}\big\rangle - \varepsilon_n(\boldsymbol{k}) \big\langle\chi_{{}\displaystyle_{\boldsymbol{k}\ell}}\big|\chi_{{}\displaystyle_{\boldsymbol{k}j}}\big\rangle \right] c_{\boldsymbol{k}j}^{(n)} = 0 \]
recordando que nuestras hipótesis implican las expresiones compactas que obtuvimos en clase
\[ \big\langle\chi_{{}\displaystyle_{\boldsymbol{k}\ell}}\big|\chi_{{}\displaystyle_{\boldsymbol{k}j}}\big\rangle = \delta_{j,\ell} \qquad {\mbox y} \qquad \big\langle\chi_{{}\displaystyle_{\boldsymbol{k}\ell}}\big| \hat{H} \big|\chi_{{}\displaystyle_{\boldsymbol{k}j}}\big\rangle = \varepsilon_j\,\delta_{\ell,j} + \sum_{\rm pv}V_{j\ell}\, e^{i\boldsymbol{k}\cdot\boldsymbol{d}_{\rm pv}} \;, \]
donde la suma es solo sobre primeros vecinos.
Como siempre, estas ecuaciones involucran las autoenergías $\varepsilon_{A,B} = \big\langle \phi_{A,B}(x) \big| \hat{H} \big| \phi_{A,B}(x)) \big\rangle$. Para garantizar soluciones no triviales exigimos que el determinante de la matriz precedente se anule, con lo que arribamos a la ecuación de autovalores
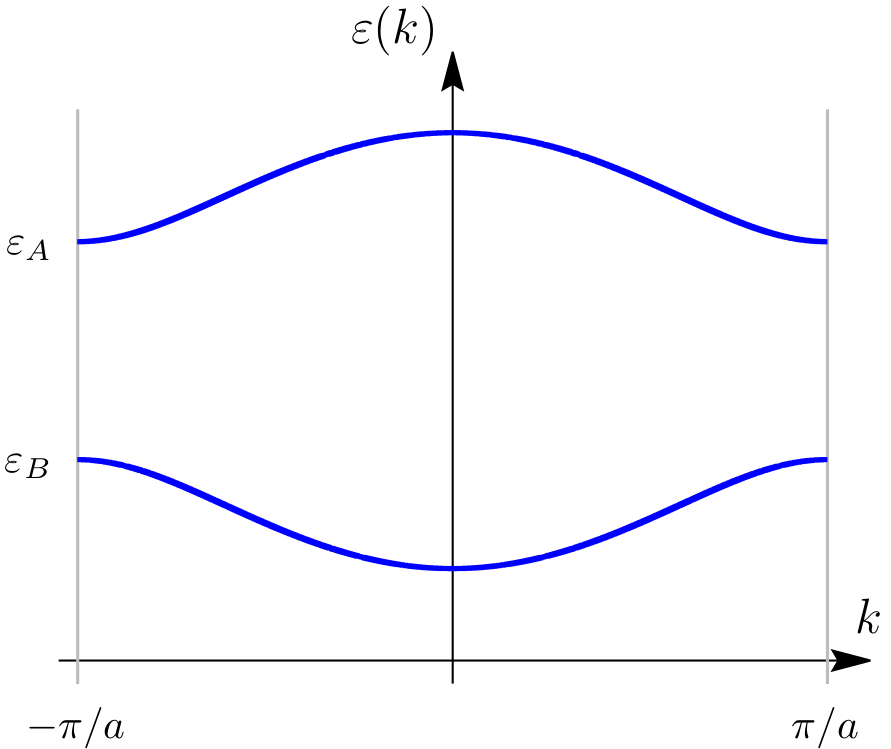
\[ \varepsilon(k) = \frac{\varepsilon_A+\varepsilon_B}{2} \pm \sqrt{ \left(\frac{\varepsilon_A-\varepsilon_B}{2}\right)^2 + \left(2\gamma\cos\frac{ka}{2}\right)^2 } \;. \]

Para el caso de un electrón de valencia por ion, como la primera zona de Brillouin puede alojar $2N$ estados (dos orientaciones de espín), en el estado fundamental la banda inferior se completa y la superior queda vacía, por lo cual este material resulta aislante. En ese caso la energía de Fermi se ubica exactamente a mitad de camino entre $\varepsilon_B$ y $\varepsilon_A$: es interesante notar que las bandas no quedan centradas en las autoenergías de los átomos aislados, sino que estas son las energías mínima y máxima de las bandas superior e inferior respectivamente.
(¿Y qué pasa cuando cada sitio aporta un electrón de valencia?)
De manera análoga al estudio que realizamos para el sólido unidimensional monoatómico (también con un solo orbital), se puede analizar la densidad de estados y señalar las singularidades de van Hove, las que también pueden inferirse de las curvas anteriores. La resolución es sencilla, y aquí solo ilustramos esta DOS mediante la gráfica siguiente.
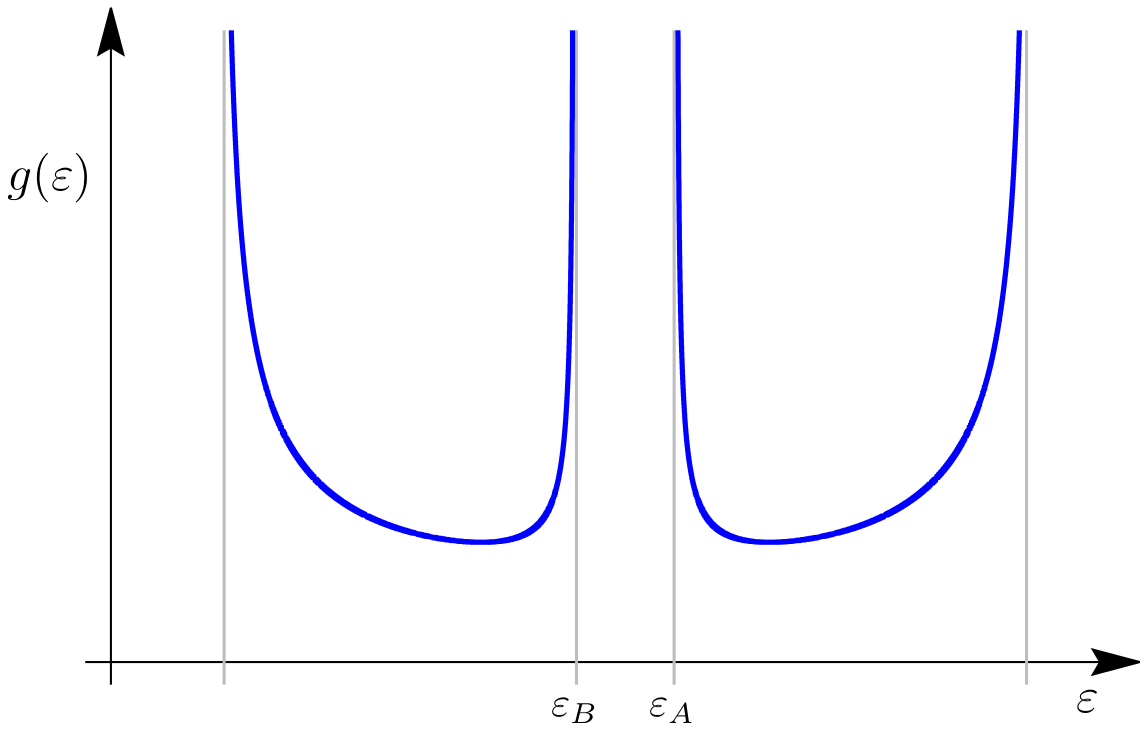
Finalmente, se deja como ejercicio verificar que en el límite $\varepsilon_B\to\varepsilon_A$ se recuperan las relaciones de dispersión que obtuvimos para el sólido unidimensional monoatómico (teniendo la precaución de considerar como nuevo parámetro de red la magnitud $d$ en lugar de $a$).