Sobre los cálculos de brechas de energías en un potencial periódico débil
Habíamos expandido las funciones de onda para un determinado valor de \(\boldsymbol{k}\,\) utilizando las ondas de Bloch
\[ \psi_{\boldsymbol{k}}(\boldsymbol{r}) = \sum_{\boldsymbol{G}}c_{\boldsymbol{k}+\boldsymbol{G}}\,e^{i(\boldsymbol{k}+\boldsymbol{G})\cdot\boldsymbol{r}} \;, \]
donde la suma abarca (en principio) todos los vectores \(\boldsymbol{G}\,\) de la red recíproca. Entonces, la resolución de la ecuación de Schrödinger sobre \(\psi\) equivale resolver un sistema de ecuaciones sobre los coeficientes \(c_{\boldsymbol{k}}\)
\[ \begin{equation}\label{Schr-k} \left(\frac{\hbar^2k^2}{2m} - \varepsilon\right) c_{\boldsymbol{k}} + \sum_{\boldsymbol{G}}U_{\boldsymbol{G}}\,c_{\boldsymbol{k}-\boldsymbol{G}} = 0\;. \end{equation} \]
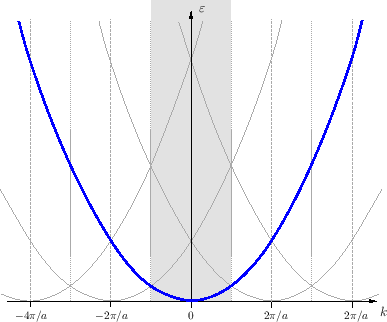
El análisis que desarrollamos nos permitió concluir que los estados \(k\) conectados en este sistema eran aquellos que se aproximan al borde de las diferentes zonas de Brillouin (planos de Bragg), o lo que es equivalente, estados en los que se cumple la condición de Laue. Si bien es directo delimitar las zonas de Brillouin en un problema sencillo, conviene dejar en claro cuáles son los \(k\) conectados en la expresión anterior. Para ello consideremos un problema unidimensional, en el cual expandimos el potencial periódico \(U(x)\) respetando la periodicidad \(a\) de la red de Bravais
\[ U(x) = \sum_{G} U_G\,e^{iGx} \;, \]
donde sumamos sobre todos los vectores (1D) \(G\!=\!2\pi m/a\) de la red recíproca. En este caso, los "planos de Bragg" que delimitan la PZB son simplemente los puntos a mitad de camino entre \(k\!=\!0\) y \(k\!=\!\pm2\pi/a\,\) (es decir, los puntos \(k\!=\!\pm\pi/a\,\)).
|
En el esquema extendido están permitidos todos los valores de \(k\), aunque sabemos que la información provista siempre puede trasladarse a la PZB. En este esquema (que no es exactamente el que se desarrolla en el texto de Ashcroft & Mermin), trabajamos con la ecuación anterior para los \(c_{\boldsymbol{k}}\), permitiendo cualquier valor para \(k\), sabiendo que la degeneración de interés ocurre en los planos de Bragg, es decir en \(k_n\!=\!\pm n\pi/a\). Veamos el caso de \(k_1\!=\!+\pi/a\,\): allí la energía \(\varepsilon_1\!=\!\hbar^2k_1^2/(2m)\) de la partícula libre es compartida por el estado \(k_{-1}\!=\!-\pi/a\), de manera que en la ecuación de arriba por un lado interviene \(k\!=\!k_1\), cuyo estado se conecta con \(k_{-1}\) mediante un único sumando con \(G\!=\!+2\pi/a\) (\(k_1\!-\!G\!=\!-\pi/a\!=\!k_{-1}\)); y por el otro, el estado con \(k\!=\!k_{-1}\) se vincula al estado \(k_1\) a través de un solo sumando con \(G\!=\!-2\pi/a\) (ahora \(k_{-1}\!-\!G\!=\!+\pi/a\!=\!k_1\)). Para esta energía hay solo dos ecuaciones como la anterior que conforman el sistema
|
|
\[
\left\{ \begin{array}{cccclll}
\left(\varepsilon_1-\varepsilon\right) c_{+\pi/a} & + &
U_{+2\pi/a}\,c_{-\pi/a} &=& 0 &\qquad& \left( \displaystyle k=+\frac{\pi}{a} \right) \\
&&&&&& \\
U_{-2\pi/a}\,c_{+\pi/a} & + &
\left(\varepsilon_1-\varepsilon\right) c_{-\pi/a} &=& 0 && \left( \displaystyle k=-\frac{\pi}{a} \right)
\end{array} \right.
\]
Tomemos la próxima energía que merece nuestra atención, para \(k_2\!=\!+2\pi/a\,\). La energía de electrón libre \(\varepsilon_2\!=\!\hbar^2k_2^2/(2m)\) se comparte con el estado con \(k_{-2}\!=\!-2\pi/a\): nuevamente notamos que la ecuación para los \(c_{\boldsymbol{k}}\) vincula a \(k\!=\!k_2\) con un único sumando en el que participa \(k_{-2}\), en este caso mediante un vector \(G\) de la red recíproca que permita cumplir \(k_2\!-\!G\!=\!k_{-2}\), es decir
\[
+\frac{2\pi}{a} - G = -\frac{2\pi}{a} \qquad\Rightarrow\qquad G = \frac{4\pi}{a} \;. \]
A continuación planteamos la situación análoga en que \(k\!=\!k_{-2}\), que comparte su energía de partícula libre con \(k_2\), en cuyo caso el planteo nos conduce a \(G\!=\!-4\pi/a\), de manera que construimos el sistema de ecuaciones
\[
\left\{ \begin{array}{cccclll}
\left(\varepsilon_2-\varepsilon\right) c_{+2\pi/a} & + &
U_{+4\pi/a}\,c_{-2\pi/a} &=& 0 &\qquad& \left( \displaystyle k=+\frac{2\pi}{a} \right) \\
&&&&&& \\
U_{-4\pi/a}\,c_{+2\pi/a} & + &
\left(\varepsilon_2-\varepsilon\right) c_{-2\pi/a} &=& 0 && \left( \displaystyle k=-\frac{2\pi}{a} \right)
\end{array} \right. \label{2pi_a}
\]
Vale la pena recordar que por construcción, \(U_{-G}\!=\!\left(U_{+G}\right)^*\), y que cuando el potencial \(U(x)\) es par (como suele ocurrir en los problemas que encaramos aquí), esto se reduce a \(U_{-G}\!=\!U_{+G}\).
|
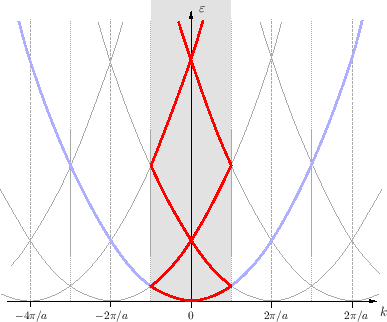
Realizamos a continuación el mismo análisis pero en el esquema reducido: ahora solo admitimos \(\boldsymbol{k}\) en la PZB, y cualquier estado análogo lo fabricamos sumando un vector de la red recíproca que nos lleve a la zona de Brillouin que nos interesa describir. Utilizamos entonces los vectores auxiliares \(\boldsymbol{M}\) de la red recíproca que nos permiten traer cualquier estado \(\boldsymbol{q}\) de afuera de la PZB para trabajar con \(\boldsymbol{k}\) en la PZB. Usando (casi) la notación del texto de Ashcroft & Mermin, definimos \(\boldsymbol{M}\) mediante la relación \(\boldsymbol{k}=\boldsymbol{q}+\boldsymbol{M}\), de modo que —teniendo en cuenta que el barrido de \(\boldsymbol{G}+\boldsymbol{M}\) abarca todos los vectores de la red recíproca— la ecuación para los \(c_{\boldsymbol{k}}\) se reescribe
|
|
\[
\left(\frac{\hbar^2(\boldsymbol{k}-\boldsymbol{M})^2}{2m} -
\varepsilon\right) c_{\boldsymbol{k}-\boldsymbol{M}} + \sum_{\boldsymbol{G}}U_{\boldsymbol{G}-\boldsymbol{M}}\,c_{\boldsymbol{k}-\boldsymbol{G}} = 0 \;.
\]
La diferencia entre esta ecuación y la de más arriba es que esta última solo admite vectores \(\boldsymbol{k}\) de la PZB, mientras que la anterior no tiene esa restricción: por lo demás, el contenido de ambas es equivalente. Nos convencemos mejor de esto volviendo a analizar el caso de la energía \(\varepsilon_2\) en nuestro problema 1D, que en el esquema reducido se consigue sumando \(M\) al estado \(+2\pi/a\) para traerlo a la PZB: queremos convertirlo en \(k\!=\!0\), lo que implica que
\[
\frac{2\pi}{a} + M = 0 \qquad\Rightarrow\qquad M = -\frac{2\pi}{a} \;.
\]
El único término que se acopla con la misma energía es el que resulta \(-2\pi/a\), ya que \(\varepsilon_{-2}=\varepsilon_2\); dicho término aparece cuando \(k-G=0-G=-2\pi/a\), es decir \(G=2\pi/a\) y en este caso \(G-M=4\pi/a\), de modo que solo aporta el coeficiente \(U_{4\pi/a}\) en la sumatoria (\(U_{4\pi/a}\,c_{-2\pi/a}\)). Un planteo similar surge cuando consideramos el estado \(-2\pi/a\) (que obviamente comparte la \(\varepsilon\)): para traerlo a la PZB (\(k\!=\!0\)) sumamos \(M\)
\[
-\frac{2\pi}{a} + M = 0 \qquad\Rightarrow\qquad M = +\frac{2\pi}{a} \;,
\]
y continuando el razonamiento vemos que en este caso \(G=-2\pi/a\) (ejercicio), con lo cual completamos el sistema de ecuaciones, que coincide con el construido anteriormente con el esquema extendido.
\[
\frac{2\pi}{a} + M = 0 \qquad\Rightarrow\qquad M = -\frac{2\pi}{a} \;.
\]
Analicemos también en el esquema reducido la próxima energía degenerada, \(\varepsilon_3=\hbar^2(3\pi/a)^2/(2m)\). Este estado se representa en la PZB con \(k=+\pi/a\) (por comodidad elegimos componentes positivas para \(k\)), de modo que
\[
\frac{3\pi}{a} + M = \frac{\pi}{a} \qquad\Rightarrow\qquad M = -\frac{2\pi}{a} \;.
\]
El único sumando que debe aparecer en la sumatoria asociado con \(-3\pi/a\!=\! k-G=\pi/a-G\), con lo cual \(G=4\pi/a\). Reuniendo todos estos ingredientes construimos el sistema de ecuaciones para \(c_{3\pi/a}\) y \(c_{-3\pi/a}\)
\[
\left\{ \begin{array}{cccclll}
\left(\varepsilon_3-\varepsilon\right) c_{+3\pi/a} & + &
U_{+6\pi/a}\,c_{-3\pi/a} &=& 0 &\qquad& \left( \displaystyle k-M=+\frac{3\pi}{a} \right) \\
&&&&&& \\
U_{-6\pi/a}\,c_{+3\pi/a} & + &
\left(\varepsilon_3-\varepsilon\right) c_{-3\pi/a} &=& 0 && \left( \displaystyle k-M=-\frac{3\pi}{a} \right)
\end{array} \right. %\label{3pi_a}
\]
La elección del esquema para realizar la construcción de estas ecuaciones depende de las preferencias de cada uno. Conviene enfatizar que si recuperamos el planteo que hicimos para el caso general en que un estado \(\boldsymbol{k}_1\) (en el esquema extendido) se conectaba a otro con igual energía mediante un vector \(\boldsymbol{G}_1\), la construcción del sistema de ecuaciones al que arribamos
\[
\left\{ \begin{array}{cccl}
\displaystyle\left(\frac{\hbar^2 k_1^2}{2m} -
\varepsilon\right) c_{\boldsymbol{k}_1} &+& U_{\boldsymbol{G}_1}\,c_{\boldsymbol{k}_1-\boldsymbol{G}_1} &= 0 \\
&&& \\
U_{-\boldsymbol{G}_1}\,c_{\boldsymbol{k}_1} &+&
\displaystyle\left(\frac{\hbar^2 |\boldsymbol{k}_1\!-\!\boldsymbol{G}_1|^2\!}{2m} -
\varepsilon\right) c_{\boldsymbol{k}_1\!-\!\boldsymbol{G}_1} &= 0
\end{array} \right.
\]
es equivalente a los de más arriba: siempre podemos comenzar desde este punto y obtener directamente las soluciones correctas.

