Siguiente: Algunos ejemplos de sistemas Subir: Condiciones para el equilibrio Anterior: Equilibrio químico
La propiedad de homogeneidad de primer orden de la ecuación fundamental
permite escribir esta relación de una manera muy conveniente. Para ello
recordemos que esta homogeneidad significa que
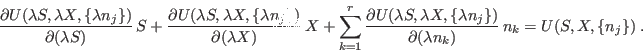
![\begin{displaymath}
{\fbox{ $\displaystyle U = T S + Y X + \sum_{k=1}^r \mu_k n_k
\rule[-1.8em]{0em}{4em}$ } }
\end{displaymath}](img169.png)
![\begin{displaymath}
{\fbox{ $\displaystyle S = \frac1T U - \frac YT X - \sum_{k=1}^r
\frac{\mu_k}T n_k \rule[-1.8em]{0em}{4em}$ } }
\end{displaymath}](img170.png)
A través de estas expresiones puede hallarse una relación entre los
parámetros intensivos de un sistema. Para ello tomamos el diferencial de ![]() :
:
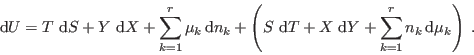
![\begin{displaymath}
{\fbox{ $\displaystyle S {\rm d}T+X {\rm d}Y+\su...
...^r n_k {\rm d}\mu_k = 0
\rule[-1.8em]{0em}{4em}$ } }
\end{displaymath}](img172.png)
Para un sistema gaseoso simple monocomponente, esta relación toma la forma
En la representación entropía la relación de Gibbs-Duhem se deduce
análogamente, y se escribe
![\begin{displaymath}
{\fbox{ $\displaystyle U {\rm d}\!\left(\frac1T\righ...
...(\frac{\mu_k}T\right) = 0
\rule[-1.8em]{0em}{4em}$ } }
\end{displaymath}](img175.png)
En un sistema termodinámico cualquiera, el número de parámetros intensivos que pueden variar independientemente constituye el número de grados de libertad termodinámicos. Es importante entonces notar que, así como en el ejemplo mencionado más arriba, las ecuaciones de estado correspondientes a un sistema termodinámico cualquiera están siempre conectadas entre sí a través de la relación de Gibbs-Duhem.
Vemos que matemáticamente podemos siempre expresar ![]() en términos de
variables termodinámicas diferentes de
en términos de
variables termodinámicas diferentes de ![]() haciendo uso de las
ecuaciones de estado. Un caso habitual es utilizar
haciendo uso de las
ecuaciones de estado. Un caso habitual es utilizar ![]() como función de
como función de
![]() . Sin embargo, es importante resaltar que ésta no sería una
relación fundamental, ya que no contiene toda la información termodinámica
posible. Para poner esto en evidencia, notemos que como
. Sin embargo, es importante resaltar que ésta no sería una
relación fundamental, ya que no contiene toda la información termodinámica
posible. Para poner esto en evidencia, notemos que como
![]() , entonces
, entonces
![]() es una ecuación en derivadas
parciales para
es una ecuación en derivadas
parciales para ![]() , de manera que, aunque la integremos, nos faltará conocer
funciones indeterminadas que surgen en el proceso de integración.
, de manera que, aunque la integremos, nos faltará conocer
funciones indeterminadas que surgen en el proceso de integración.
Gustavo Castellano 06/06/2013