Fluido ideal de Van der Waals
Los gases reales se comportan como gases ideales sólo a bajas densidades.
Una mejor descripción se logra utilizando la ecuación de estado
donde 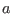 y
y 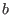 son constantes características de cada gas. Esta ecuación
representa cualitativamente bien el comportamiento de muchos fluidos, e
incluso resulta adecuada para incluir la transición de fase líquido-gas. En
realidad esta expresión surge como modificación a la ecuación para los gases
ideales. El parámetro
son constantes características de cada gas. Esta ecuación
representa cualitativamente bien el comportamiento de muchos fluidos, e
incluso resulta adecuada para incluir la transición de fase líquido-gas. En
realidad esta expresión surge como modificación a la ecuación para los gases
ideales. El parámetro 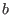 contempla la primera corrección, que surge a raíz
de que las moléculas de un gas no son masas puntuales, sino que cada una
ocupa cierto volumen
contempla la primera corrección, que surge a raíz
de que las moléculas de un gas no son masas puntuales, sino que cada una
ocupa cierto volumen 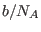 ; de este modo el volumen disponible para cada
partícula no es el volumen
; de este modo el volumen disponible para cada
partícula no es el volumen 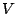 del recipiente, sino que es reducido a
del recipiente, sino que es reducido a
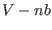 . La segunda corrección (
. La segunda corrección (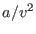 ) está relacionada con la interacción
entre las moléculas: cerca de las paredes del recipiente las moléculas no
experimentan una fuerza resultante nula, sino que son atraídas por el resto
de las moléculas hacia el interior. Esta reducción de la presión debe ser
proporcional al número de pares de moléculas interactuantes, o sea al
cuadrado del número de moléculas por unidad de volumen
) está relacionada con la interacción
entre las moléculas: cerca de las paredes del recipiente las moléculas no
experimentan una fuerza resultante nula, sino que son atraídas por el resto
de las moléculas hacia el interior. Esta reducción de la presión debe ser
proporcional al número de pares de moléculas interactuantes, o sea al
cuadrado del número de moléculas por unidad de volumen 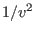 .
.
Para definir completamente nuestro sistema debemos agregar a la ecuación de
estado ``mecánica'' una ecuación de estado ``térmica''. Es decir, contamos
con la ecuación
y nos falta una relación del tipo
para poder integrar
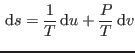 .
Para construir esta relación, notemos que para que
.
Para construir esta relación, notemos que para que 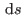 sea un diferencial
exacto, debe cumplirse
sea un diferencial
exacto, debe cumplirse
Como
la igualdad anterior puede escribirse
es decir que 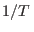 depende de las variables
depende de las variables 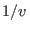 y
y 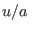 de manera
tal que al derivar con respecto a cada una de ellas se obtiene la misma
expresión. Esto puede suceder si
de manera
tal que al derivar con respecto a cada una de ellas se obtiene la misma
expresión. Esto puede suceder si 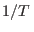 es función sencilla de
es función sencilla de 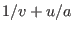 .
Como buscamos corregir la expresión que teníamos para el gas ideal, para el
que se cumple
.
Como buscamos corregir la expresión que teníamos para el gas ideal, para el
que se cumple 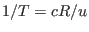 , lo más natural parece ser adecuarla escribiendo
, lo más natural parece ser adecuarla escribiendo
Con esta segunda ecuación de estado se completa la descripción para el
fluido de Van der Waals. Combinando las dos ecuaciones de estado puede
escribirse la relación mecánica en términos de 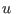 y
y 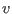 :
:
Ahora sí, estamos en condiciones de integrar la expresión diferencial para
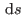 . Queda como ejercicio mostrar que la ecuación fundamental resulta
. Queda como ejercicio mostrar que la ecuación fundamental resulta
Al igual que en el caso del gas ideal, esta ecuación fundamental
no satisface el postulado de Nernst (las dos verificaciones se
dejan también como ejercicios). Esto significa que no puede esperarse una
buena descripción termodinámica a bajas temperaturas, lo que no implica
ningún contratiempo, ya que de antemano sabíamos que ésta era una
limitación para ambos modelos.
El último comentario que hacemos sobre el fluido de Van der Waals es que la
descripción que se logra presenta regiones ``inestables'' para ciertas
temperaturas. Como veremos más adelante, esto significa que el fluido se
separa espontáneamente en dos fases, una líquida y otra gaseosa.
Gustavo Castellano 06/06/2013
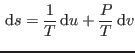 .
Para construir esta relación, notemos que para que
.
Para construir esta relación, notemos que para que 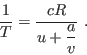
![\begin{displaymath}
\fbox{ $S = \displaystyle nR \ln \left[ (v-b)
\left( ...
...right)^c \right] + n s_o \;. \rule[-1.75em]{0em}{4em}$ }
\end{displaymath}](img243.png)