Análisis Numérico

Trabajo de Laboratorio N$^\circ$ 1 (Versión para lenguaje $C$)

Ejercicios Obligatorios

Problema 1: Evaluar (en papel y lápiz) las siguientes expresiones:

1. 5 / 2 + 20 % 6
2. 4 * 6 / 2 - 15 / 2
3. 5 * 15 / 2 / (4 - 2)
4. 8 == 16 || 7 != 4 && 4 < 1
5. (4 * 3 < 6 || 3 > 5 - 2) && 3 + 2 < 12

Problema 2: Escribir un programa que pida dos números reales e imprima en la pantalla el mayor de ellos. El programa debe indicar si los números son iguales.

Problema 3: Escribir un programa que pida un número entero y determine si es múltiplo de 2 y de 5.

Problema 4: Escriba una programa que ingrese los coeficientes $A$, $B$ y $C$ de un polinomio real de segundo grado ( $A x^2 + B x + C$), calcule e imprima en pantalla las dos raíces del polinomio en formato complejo $a + i b$.

Problema 5: Diseñar una función que calcule la potencia enésima de un número, es decir que devuelva $X^n$ para $X$ real y $n$ entero. Realice un programa que utilice la función e imprima en pantalla las primeras 5 potencias naturales de un número ingresado.

Problema 6: Se pretende calcular las sumas $S_N = \sum_{k=1}^N a_k$, donde $N$ es un número natural. Llamemos $S^{\prime}_N$ al valor calculado que se logra de hacer (float) $(S_{N-1} + a_N)$. Sea $S_N = \sum_{k=1}^N 1/k$. Mostrar que $S^{\prime}_N$ se estaciona a partir de algún $N$ suficientemente grande. Deducir que a partir de entonces $S_N \neq S_N^{\prime}$. Hacer un programa que determine el valor a partir del cual $S_N^{\prime}$ se estaciona.

Problema 7: Escriba un programa para calcular un valor aproximado de $\pi$ utilizando la productoria de Wallis

$$\frac{\pi}{2} = \prod_{n=1}^\infty \frac{(2n)^2}{(2n)^2-1} = \frac21\frac23\frac43\frac45\frac65\frac67\dots$$

Calcule el valor de $\pi$ truncando la productoria a $10^6$ factores.

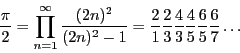
Ejercicios Complementarios

Problema 8: Escribir un programa que permita jugar a doble o nada: el jugador apuesta una cantidad y tira una moneda. Si sale cara obtiene el doble de la cantidad apostada. Si sale cruz la pierde todo.

Problema 9: Para calcular un valor aproximado de $\pi$ utilizaremos la siguiente serie infinita alternante

$$\sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} = \frac{\pi}{4}$$ (1)

Recordemos que una cota superior para el error cometido al truncar una serie alternante (de valor absoluto decreciente) está dado por el valor absoluto del primer término despreciado. Escriba un programa que ingrese el número de cifras decimales exactas con que se desea el valor de $\pi$ (entre 1 y 5 cifras) y devuelva en pantalla el número de términos que deben incluirse en la serie (1) para obtener dicha precisión y a renglón siguiente el valor de $\pi$ obtenido de esta forma, truncado el resultado al múmero de cifras pedido.

Problema 10: Escribir un programa para jugar a adivinar un número entero entre 1 y 10 (generado al azar por el ordenador). Su salida debe ser el número de intentos.

Problema 11: Escribir un programa que pida un número e imprima por pantalla su tabla de sumar.

Problema 12: Escribir un programa que pida una contraseña de tres dígitos y permita leer tres intentos. Si el usuario da la contraseña correcta responde responde ``Correcto'' y queda inactivo, con este mensaje. En caso contrario el programa escribe ``Lo siento, contraseña equivocada'' y se cierra de inmediato.

Problema 13: Escribir un programa que, dado un año y el nombre de un mes, saque por pantalla el número de dias del mes (tenga en cuenta que algunos años son bisiestos).