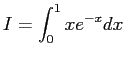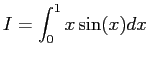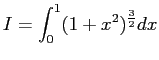Análisis Numérico

Trabajo de Laboratorio N$^\circ$ 3

Integración Numérica

Problema 1: a) Realice un programa que integre numéricamente la función

$$I = \int _0 ^1 e^{-x} dx$$

utilizando optativamente la regla compuesta del trapecio o la regla compuesta de Simpson. El intervalo de integración debe ser dividido en $N$ subintervalos del mismo tamaño $h$. La salida debe ser la aproximación $S$ obtenida.

b) Calcule, utilizando el programa del punto anterior, el error $\varepsilon(h)=\vert S-I\vert$, para $h=0.05$ y $h=0.025$. Verifique que el cociente de precisión

$$Q = \frac{\varepsilon(h)}{\varepsilon(h/2)}$$

sea aproximadamente 4 o 16, según haya usado la regla del trapecio o de Simpson, respectivamente.

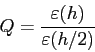
Ejercicios Complementarios

Problema 2: Realice un programa que integre numéricamente una función $f$ en un intervalo $[a,x]$ utilizando la regla compuesta del trapecio corregida.

Problema 3: Aplique el programa del ejercicio anterior para integrar $f(x) = \cos(x)$ entre $0$ y $x$, generando un tabla de valores con dos columnas, $x$ y $S(x)$, donde $S(x)$ es la aproximación numérica a a integral

$$I(x) = \int_0^x \cos(u)~du,$$

Grafique usando gnuplot $\sin(x)$ y $S(x)$ vs. $x$, simultáneamente.

Problema 4: Calcular mediante las reglas del trapecio compuestas, la regla de Simpson compuesta, y la regla del trapecio corregido compuesta, las siguientes integrales, con 6 dígitos correctos.

1. $I = \displaystyle{\int _0 ^1 x e^{-x} dx}$

2. $I = \displaystyle{\int _0 ^1 x \sin (x) dx}$

3. $I = \displaystyle{\int _0 ^1 ( 1 + x^2 )^{\frac{3}{2}} dx}$