Next: About this document ...
Problema 1:
Realizá un programa en C que te permita resolver numéricamente
el problema de valores iniciales de la forma,
Problema 2:
Utilizando el programa del ejercicio anterior, resolvé mediane el método
de Euler el siguiente problema de valores iniciales:
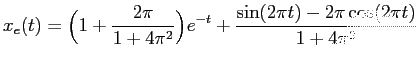
Problema 3:
Realizá un programa en C que te permita resolver numéricamente
el problema de valores iniciales de la forma
Problema 4: Repetí el problema 3, pero esta vez usando el método de Runge-Kutta de
4![]() orden en lugar del método de Euler.
orden en lugar del método de Euler.
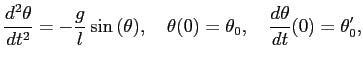
| (1) | ||
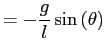 |
(2) |
Modificá el programa del ejercicio 3 de forma tal que resuelva ahora este sistema
de dos ecuaciones diferenciales ordinarias acopladas usando
![]() y
y ![]() La salida debe ser un archivo de tres columnas
La salida debe ser un archivo de tres columnas ![]() ,
, ![]() y
y ![]() .
.
Problema 6:
La llamada ecuación logística
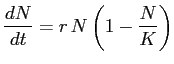
Una solución ![]() se dice estacionaria si se satisface que
se dice estacionaria si se satisface que ![]() , y por
ende no cambia en el tiempo. Para esta ecuación es fácil verificar que
sólo existen dos soluciones estacionarias:
, y por
ende no cambia en el tiempo. Para esta ecuación es fácil verificar que
sólo existen dos soluciones estacionarias: ![]() y
y ![]() .
.
Determiná cual de las dos soluciones estacionarias es estable y cual inestable
resolviendo numéricamente la ecuación diferencial con el método
Runge-Kutta de cuarto orden para ![]() ,
, ![]() , en el intervalo
, en el intervalo
![]() con
con ![]() y considerando cinco condiciones iniciales diferentes: a)
y considerando cinco condiciones iniciales diferentes: a) ![]() ,
b)
,
b) ![]() , c)
, c) ![]() , d)
, d) ![]() y d)
y d) ![]() . Graficá
simultaneamente las cinco soluciones
. Graficá
simultaneamente las cinco soluciones ![]() vs.
vs. ![]() en el intevalo
en el intevalo
![]() .
.