Análisis Numérico

Trabajo de Laboratorio N$^\circ$ 6

Problema 1: Desarrolle un programa que implemente, optativamente, el método de Jacobi o el método de Gauss-Seidel para resolver el sistema lineal $A \vec{x} = \vec{b}$.

Los datos de entrada deben ser la tolerancia $\delta$ y el número máximo permitido de iteraciones.

El programa debe leer los valores de las entradas de $A$, $\vec{b}$ y de la iteración inicial $\vec{x}_0$ de tres archivos de datos.

Para cada iteración, el programa debe imprimir en pantalla el número $s$ de iteración y el valor de la norma $\Vert\vec{x}^s - \vec{x}^{s-1}\Vert _1$, donde

$$\Vert\vec{x}^s\Vert _1 = \sum_{i=1}^N \vert x^s_i\vert$$

El programa debe detenerse cuando alcanza el número máximo de iteraciones o si se cumple la condición: $\Vert\vec{x}^s - \vec{x}^{s-1}\Vert _1 \le \delta$; debe imprimir además la iteración final en formato exponencial y con diez decimales.

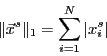
Problema 2: Aplique el programa desarrollado para resolver, mediante ambos métodos, el sistema de ecuaciones $A \vec{x} = \vec{b}$ con

$$A=\left(\begin{array}{rrrrrr} 4 & -1 & 0 & -1 & 0 & 0\\ -1 ... ...begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{array} \right)$$

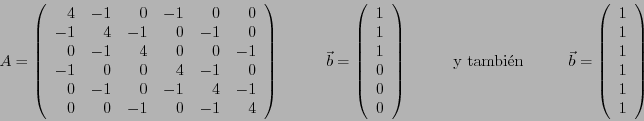
Problema 3: Decida si los métodos de Jacobi y/o Gauss-Seidel son aplicables para resolver los siguientes sistemas de ecuaciones. En cada caso afirmativo calcule las soluciones, en el caso (a) con $\delta = 10^{-11}$, en el caso (b) con $\delta = 10^{-4}$. >Cuántas iteraciones son necesarias en cada caso para alcanzar la precisión deseada?

$$\mbox{\bf (a)} \;\; \left(\begin{array}{ccc} 3 & 1 & 1\\ 2 ... ...left(\begin{array}{c} 23 \\ 32 \\ 33 \\ 31 \end{array} \right)$$

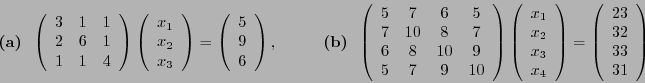
Ejercicios Complementarios

Problema 4: Modifique el programa que implementa el método de Jacobi para que guarde en las sucesivas filas de un archivo de salida los valores de las iteraciones $\vec{x}^s$. Utilizando este programa resuelva el sistema con

$$A = \left(\begin{array}{cc} 2 & 1\\ 3 & 6 \end{array}\right... ...} \vec{b} = \left(\begin{array}{c} 8 \\ 21 \end{array}\right)$$

con los distintos valores iniciales

$$\mbox{\bf (a)} \;\; \vec{x}^0 = \left(\begin{array}{c} 1 \\ ... ...\vec{x}^0 = \left(\begin{array}{c} 5 \\ 2 \end{array}\right)$$

Finalmente grafique los puntos de las sucesiones de iteraciones obtenidas usando gnuplot.