Fundamentos básicos del procesamiento de imágenes¶

Una vez presentadas las bases físicas que dan lugar a la formación de las imágenes radiológicas, en el presente Capítulo se introducirán los primeros conceptos básicos y la formulación matemática necesaria para un acercamiento al procesamiento de imágenes digitales. Así, se introducirá al lector en las primeras nociones para lograr comprender la representación y las operaciones elementales del procesamiento digital de imágenes.

Introducción al procesamiento de imágenes¶

El análisis y procesamiento de imágenes se realiza a través de computadoras, debido a la complejidad y el número de cálculos necesarios para realizarlo. Es por esto que, si bien la formulación matemática necesaria para su realización data de varios siglos atrás, la posibilidad real de utilizarla de forma cotidiana en la práctica clínica ha sido posible recién en las últimas décadas, gracias al avance en las tecnologías del hardware.

La proliferación de nuevos equipamientos con capacidad para realizar millones de operaciones por segundo y su extensión a la vida cotidiana y a todo tipo de usuario, ha hecho posible que el análisis y procesamiento de imágenes digitales se constituya en un gran campo de estudio. En la actualidad, esta tecnología se encuentra incorporada incluso en todo tipo de equipamiento doméstico, como cámaras digitales, scaners y teléfonos celulares, entre otros.

En términos históricos, la utilización de imágenes radiográficas para diagnóstico clínico data prácticamente desde el descubrimiento de los rayos X en 1895 (Röentgen). Incluso, las imágenes funcionales a partir de la emisión de fotones (rayos $\gamma$) por parte de radionucleidos ya cuenta con más de 90 años de antigüedad (Heavesy & Seaborg, 1924). Sin embargo, las imágenes eran adquiridas sobre films radiográficos o directamente in vivo, por lo que su correcto procesamiento no ha explotado su real potencialidad sino hasta la incorporación de la tecnología que permitió digitalizarlas.

El motivo principal de esta “aparición tardía” del procesamiento de imágenes ha sido entonces, debido a los requerimientos de hardware tanto para el procesamiento de las mismas como para la representación de estas en sistemas gráficos de alta performance. Paralelamente a este desarrollo, la formulación de algoritmos para el procesamiento ha seguido los avances tecnológicos logrando un alto grado de sofisticación y manipulación de imágenes en tiempo casi real.

La variedad actual de técnicas, algoritmos y desarrollos de software y hardware utilizados en el procesamiento de imágenes digitales escapa al alcance de cualquier curso. En ellos se aprovechan técnicas desarrolladas inicialmente sobre conceptos fundacionales para el análisis de imágenes, y se incorporan conceptos y nociones de los más variados, propios de la física y la matemática, como el caso de la entropía o la métrica.

En el presente capítulo se introducirán las primeras nociones y conceptos para abordar el estudio del procesamiento de imágenes digitales, entre los que se cuentan las formatos de lectura y representación de imágenes, las operaciones de modificación, las transformaciones sobre tonalidades y colores, y la generación de efectos sobre regiones de una imagen.

El interés del siguiente estudio puede condensarse en dos objetivos principales: a) lograr una mejora considerable de la calidad de la imagen para la interpretación de un especialista, y/o b) lograr la obtención de información específica para su procesamiento por medio de sistemas de cálculo y análisis.

Serán de interés de este curso, las imágenes producidas por interacción de la radiación ionizante con la materia para uso médico, es decir aquellas adquiridas por detectores de rayos X o $\gamma$ [1] y que hayan atravesado -o partido de- tejido biológico de un paciente, formando una imagen bidimensional (2D) o tridimensional (3D).

Formato de imagen y representación digital¶

En la actualidad, las imágenes constituyen un lenguaje en sí mismas. Dependiendo de diferentes factores culturales, las imágenes son utilizadas para transmitir mensajes, símbolos y distintos tipos de información. Por esto, es necesario contar con un soporte para la representación digital de las imágenes que permita luego modificar el mismo a fin de o bien modificar el contenido visual y simbólico u obtener información necesaria.

Bandas en imágenes digitales¶

Para lograr adquirir una imagen, de forma remota, debe existir algún tipo de interacción entre el objeto que se desea observar y el detector. En las imágenes digitales, los distintos tipos de detector dependen del tipo de radiación electromagnética que son capaces de detectar. Así como la información que se puede obtener de un objeto depende también de la interacción de esta radiación con el objeto. De esta particularidad proviene el concepto de “bandas”, donde se divide el espectro electromagnético en función de los tipos de interacción de la radiación con la materia (ver Fig. [fig2-1]), lo que define desde los objetos a analizar hasta los detectores y materiales que pueden utilizarse.

Todos los objetos absorben, reflejan o emiten cuantos de energía dependiendo de su longitud de onda, intensidad y tipo de radiación. Este tipo de radiación se define a partir de sus propiedades físicas dentro del espectro electromagnético. El ojo humano, por su parte, solo es capaz de detectar energía electromagnética en el espectro de luz visible, mientras que para los rayos X, la radiación ultravioleta, infrarroja o de microondas, es necesaria la construcción de detectores que puedan recabar esta información, ya sea de forma digital o analógica, para poder ser cuantificada y analizada.

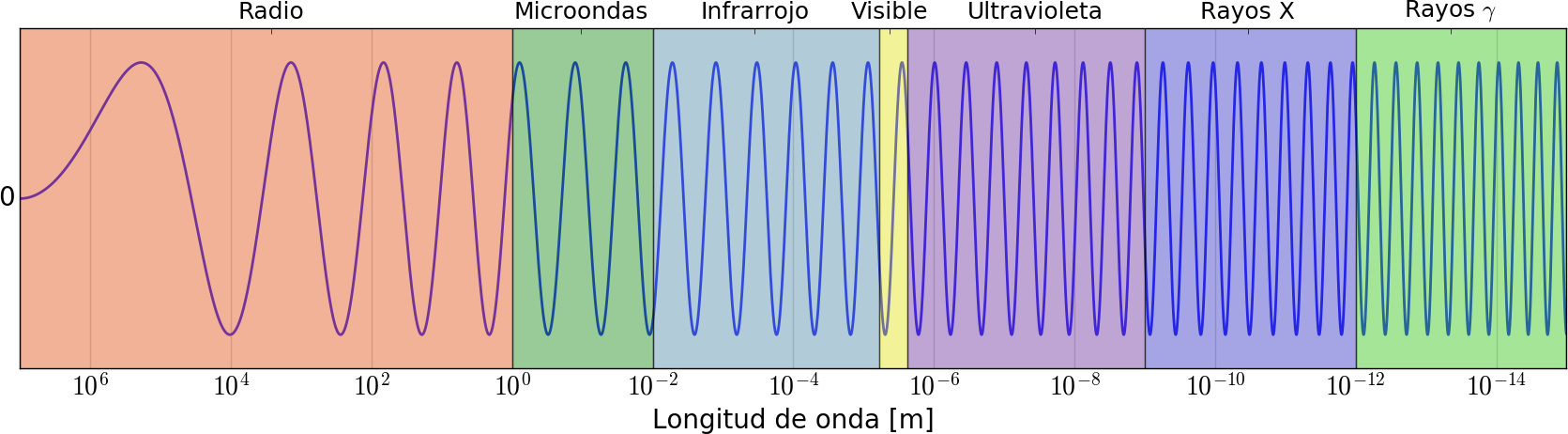
Figura 1: Esquema cualitativo del espectro electromagnético

Representación digital: mapa de bits (Bitmaps)¶

Un Bitmap es un modo elemental para representar imágenes digitales como información en el hardware, específicamente la memoria, de un computador. Consiste, básicamente, en formar arreglos de elementos (vectores, matrices, tensores) ordenados de modos específicos. En general, para el caso típico de imágenes 2D, se realiza un ordenamiento por filas de elementos de matriz (pixels) asignando a cada uno un valor que determina “el color” en esa posición de la imagen.

En el caso de imágenes en tonalidades de grises, el valor del elemento de matriz es un escalar; mientras que para el caso de imágenes a color el valor de cada elemento de matriz es un vector de tres coordenadas, cada una de las cuales especifica “el grado de influencia” de los colores rojo (Red “R”), verde (Green “G”) y azul (Blue “B”), de modo que se denomina representación RGB). Existen otros modos de representación a color, como por ejemplo CMYK (cián, magenta, amarillo y negro).

Típicamente se emplean escalas (que determinan “rangos dinámicos”) en $2^{N}$ bits, y se denomina $N-$ bits. Es decir, para el caso más común de 8-bits, la escala es $[0, 255]$, ya que por costumbre se define el rango como $[0, 2^{N} - 1]$.

El uso típico de 8-bits está basado, principalmente, en dos motivos. En primer lugar, estudios biométricos muestran que el ojo humano no es suficientemente sensible para diferenciar más de 256 niveles de intensidad para un dado color. Además, el rango de valores para los elementos de matriz determinan las necesidad en cuanto a la capacidad de almacenamiento en el computador.

Entonces, para imágenes en tonalidades de grises, conocidas como “de una banda” el rango para los valores de los elementos de matriz (escalares) es $[0, 255]$, mientras que para imágenes a color, los valores de elementos de matriz (vectores de 3 coordenadas) asumen valores en $([0, 255], [0, 255], [0, 255])$. Si embargo, también es frecuente encontrar representaciones normalizadas para imágenes a color, es decir, elementos de matriz en $([0, 1], [0, 1], [0, 1])$ para determinar los colores RGB.

Todos los colores en el rango visible pueden representarse como combinaciones RGB, variando desde el negro $(0, 0, 0)$ al blanco $(255, 255, 255)$. Por lo tanto, una imagen RGB es representada por un arreglo bidimensional de pixels, cada uno codificado en 3 bytes pudiendo asumir $256^{3}$ diferentes valores de combinaciones vectoriales, es decir 16.8 millones de diferentes colores, aproximadamente.

Representación digital: imágenes vectoriales¶

Las imágenes vectoriales están constituidas por contornos y rellenos definidos matemáticamente, vectorialmente, por medio de ecuaciones que describen perfectamente cada ilustración. De este modo, es posible implementar scaling sin pérdida de calidad. El proceso de scaling es típico en la formación, producción o reproducción en dispositivos. Por ello, la importancia de mantener la invariabilidad. Esta característica resulta de particular relevancia en casos que las ilustraciones contengan marcadas zonas con contornos curvados, ya que el pixelado implicaría una pérdida de resolución, como indica la figura .

Figura 2: Imagen en representación vectorial (izquierda) y en pixelado bitmap (derecha).

Modificación de colores en imágenes¶

Es posible cuantificar la diferencia entre dos colores (en representación digital, valores del trio vectorial RGB) calculando la distancia, según algún tipo de métrica, Euclidea por ejemplo, entre los vectores que los representan.

Se el color $C_{1}$ representado por el vector $(R_{1}, G_{1}, B_{1})$ y el color $C_{2}$ representdo por $(R_{2}, G_{2}, B_{2})$. Entonces, en el espacio vectorial, la distancia $D (C_{1}, C_{2})$ entre éstos está dada por:

\[\begin{aligned} D(C_{1}, C_{2}) = \sqrt{ \left(R_{1} - R_{2} \right)^{2} + \left(G_{1} - G_{2} \right)^{2} + \left(B_{1} - B_{2} \right)^{2}} \label{EqXXII}\end{aligned}\]

Para el caso particular de imágenes de una banda (tonalidades de grises) puede aplicar la misma metodología descrita para imágenes RGB con la simplificación asociada al hecho de que en el espacio de colores, los vectores en la dirección del vector $(1, 1, 1)$ representan las diferentes tonalidades de gris.

Por tanto, existe la equivalencia de que para cualquier pixel de tipo RGB $(R, G, B)$ si se lo proyecta sobre $(1, 1, 1)$ se obtiene la contribución de cada tonalidad de gris. Entonces, se tiene:

\[\begin{aligned} Proy \equiv (R, G, B) \cdot (1, 1, 1) =R + G + B = \lvert \vec{V} \rvert \lvert \hat{n} \rvert cos(\phi) \label{EqXXIIb}\end{aligned}\]

donde $Proy$ es la proyección, $\vec{V}$ es el vector que forma el punto $(R, G, B)$ en el espacio de coordenadas del trío (representación vectorial), $\hat{n}$ es el versor de proyección $(1, 1, 1)$ y $\phi$ es el ángulo que forma $\vec{V}$ con $\hat{n}$.

De aquí puede verse que $Proy = \frac{R + G + B}{\sqrt{3}}$ y debe atenderse de que este valor no exceda 255, de modo que es usual renormalizar para obtener $Proy = \frac{R + G + B}{3}$

A modo de ilustración de los conceptos generales expuestos sobre representaciones vectoriales-bitmap, se propone un caso de aplicación muy sencillo. Si el objetivo en la detección de bordes (orillas) de las formas en una imagen para obtener el bitmap resultante que resalte los bordes en blanco-negro, puede procederse del siguiente modo: Desplazarse dentro de la imagen pixel a pixel comparando el color de cada uno con su vecino de la derecha y su vecino de abajo. Luego, se efectúa el siguiente control (criterio): si al comparar resulta en una diferencia muy grande (“muy grande” es un parámetro [2] o conjunto de parámetros pre-definidos por el usuario, o bien automatizados en casos más elaborados) el pixel en consideración forma parte del borde y se le asigna el color blanco, de otro modo se asigna el color negro.

Histograma de una imagen¶

Dada la representación digital de una imagen por medio del arreglo de $N$ filas por $M$ columnas se determina una matriz $M \times N$, en la cual la representación digital de bitmap estará dada por la función distribución $f(m, n)$, para $n \in [0, N-1]$ y $m \in [0, M-1]$, típicamente $N$ y $M$ son potencias de 2, como ya se enunció.

El histograma de una imagen $h(i)$, comúnmente denominado “image enhancenment” o “image characterization” es un vector que da cuenta de la cantidad de pixels dentro de la imagen con un cierto valor de elemento. Es decir, para una imagen de $\alpha$-bits, se tiene:

\[\begin{aligned} h(i) \equiv \sum _{m=0}^{M-1} \, \; \sum _{n=0}^{N-1} \delta(f(n, m) - i) \; \, \; \forall i \in [0, 2^{\alpha}-1] \label{EqXXIII}\end{aligned}\]

Una de las técnicas genéricas, que luego se diversifica a una cantidad muy variada de metodologías específicas de procesamiento, es el método de convolución. Sea $w(k, l)$ un arreglo $2 \times K + 1, 2 \times L + 1$, centrado en el “origen” $(0, 0)$ que coincide con el pixel central de la imagen. Puede considerarse a $w(k, l)$ como un kernel de convolución de modo que aplicado a la imagen $f(n, m)$ resulte:

\[\begin{aligned} g(m, n) \equiv w(k, l) \ast f(m, n) = \sum _{k=-K}^{K} \, \; \sum _{l=-L}^{L} w(k, l) \cdot f(m-k, n-l) \label{EqXXIV}\end{aligned}\]

A partir de esta definición, pueden introducirse una gran cantidad de métodos específicos, entre los que se destacan las transformadas, como Fourier, Laplace, Radon, etc.

Resolución de una imagen¶

A priori, este concepto tiene diferentes acepciones según el contexto en el que se utilice y se podría definir, de modo genérico, como la capacidad para representar o percibir los detalles de una imagen. Se trata de un concepto presente en todo el proceso digital, desde la captura o generación hasta la representación, y afecta (condiciona) el procesamiento posterior.

Una definición útil es: la resolución de una imagen es la cantidad de pixels que la describen. Y una medida típica es en términos de “pixels por pulgada” (ppi). Por tanto, la calidad de la representación así como el tamaño de la imagen dependen de la resolución, que determina a su vez los reqerimientos de memoria para el archivo gráfico a generar.

Resolución, tamaño de imagen y tamaño de archivo¶

Los tres conceptos están estrechamente relacionados y dependen mutuamente, aunque se refieren a características diferenciadas y debe evitarse la confusión.

El tamaño de una imagen son sus dimensiones reales en términos de anchura y altura una vez impresa, mientras que el tamaño del archivo se refiere a la cantidad de memoria física necesaria para almacenar la información de la imagen digitalizada en cualquier soporte informático de almacenamiento.

Ciertamente, la resolución de la imagen condiciona fuertemente estos dos conceptos, ya que la cantidad de pixels de la imagen digitalizada es fijo y por tanto al aumentar el tamaño de la imagen se reduce la resolución y viceversa.

A modo de ejemplo: duplicando la resolución de una imagen digitalizada, de 50 ppi a 100 ppi, el tamaño de la imagen se reduce a la cuarta parte del original mientras que dividir la resolución por 2. Es decir, se pasa de 300 ppi a 150 ppi obteniendo una imagen con el doble de las dimensiones originales que represebtan cuatro veces su superficie.

La reducción de la resolución de la imagen, manteniendo su tamaño, provoca eliminación de pixels. Entonces, se obtiene una representación (descripción) menos precisa de la imagen, así como transiciones de color más bruscas. El tamaño del archivo que genera una imagen digitalizada es proporcional, como se espera, a la resolución, por lo tanto, variarla implica modificar en el mismo sentido el tamaño del archivo.

Contraste en una imagen¶

Conceptualmente, aumentar o disminuir el contraste en una imagen consiste, básica y visualmente, en aumentar o disminuir la pendiente de la linea recta con pendiente a 45 grados que representa los grises (con la precaución de no exceder los límites 0-255) entre input y output, como indica la figura [Fig2_2].

La transformación correspondiente al cambio de contraste es:

\[\begin{aligned} V_{O}(m, n) = \left( V_{I}(m, n) - 2^{Y - 1} \right) \, \tan{\phi} \, + 2^{Y - 1} \label{EqXXV}\end{aligned}\]

donde $Y$ es la escala en bits, $V_{I}$ y $V_{O}$ son los valores de input y output, respectivamente valuados en el pixel $(m, n)$; y el ángulo $\phi$ cooresponde a las propiedades de la transformación lineal de contrastes, específicamente la pendiente (figura [Fig2_2]).

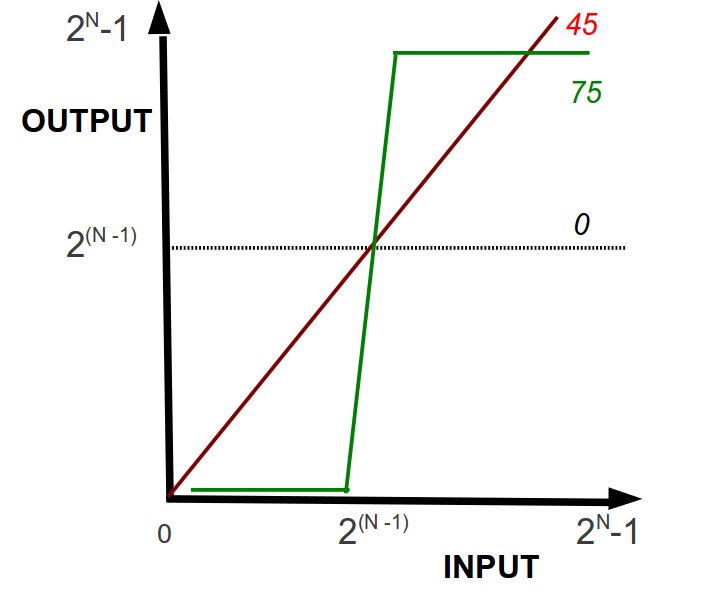
Figura 3: Representación del cambio de contraste entre input y output.

Vínculo físico del origen de imágenes¶

Las imágenes generadas por radiación electromagnética pueden clasifcarse en modo genérico según el ordenamiento de mayor a menor frecuencia.

Rayos $\gamma$: medicina nuclear, observaciones de astronomía.
Rayos X: diagnóstico médico e industria (control de calidad).
Banda ultravioleta: Inspección industrial y microscopía biológica.
Banda visible e infrarroja: Aplicaciones varias, fotografía.
Microondas: radar.
Ondas de radio: medicina (MRI) y algunas aplicaciones en astronomía.

Modificación de una imagen¶

Una imagen input puede ser modifica por medio de diferentes maneras, según la/s propiedad/es que se modifica/n.

En particular, se consideran a continuación algunas de las modificaciones más frecuentes.

Modificación de colores o tonalidades: Corrección $\gamma$¶

Existe una amplia variedad de técnicas y criterios para modificar los colores de una imagen. Una de las metodologías más empleada, y sencilla, es la corrección $\gamma$, definida a partir de:

\[\begin{aligned} V_{O}(m, n) = \left( 2^{N} - 1 \right) \left( \frac{V_{I}(m, n)}{2^{N} -1} \right)^{\frac{1}{\gamma}} \label{EqXXVI}\end{aligned}\]

donde el índice $\gamma$ asume valores $\in \Re$.

Por lo tanto, resulta:

Para $\gamma$ = 1 no hay ninguna corrección.
Para valores de $\gamma > 1$ hay una gran corrección en el contraste para valores pequeños del color de input mientras que una pequeña corrección en el contraste para valores altos. El brillo aumenta más para valores intermedios del color de input.
Para valores de $\gamma < 1$ hay una pequeña corrección en el contraste para valores bajos del color de input, mientras que una gran corrección en el contraste para valores altos. El brillo disminuye más para valores intermedios del color de input.

Modificación de imagen: inversión (flip)¶

Básicamente, esta modificación consiste en una transformación que produce un “movimiento” de la columna $m$, fila $n$ a la columna $m$ y fila $(n_{max} - n) + 1$, para $n_{max}$ como la dimensión en la dirección de $n$.

Es decir,

\[\begin{aligned} V_{flip}(m, n) = V_{I} (m, (n_{max} - n) + 1) \label{EqXXVII}\end{aligned}\]

donde $V_{flip}$ es la matriz de output que corresponde a la transformación de inversión.

Modificación de imagen: reflexión (mirror)¶

Básicamente, esta modificación consiste en una transformación que produce un “movimiento” de la fila $n$, columa $m$ a la fila $n$ y columna $(m_{max} - m) + 1$, para $m_{max}$ como la dimensión en la dirección de $m$.

Es decir,

\[\begin{aligned} V_{mirror}(m, n) = V_{I} ((m_{max} - m) + 1, n) \label{EqXXVIII}\end{aligned}\]

donde $V_{mirror}$ es la matriz de output que corresponde a la transformación de reflexión.

Modificación de imagen: interpolación¶

A partir de de un muestreo input pueden estimarse los valores de la intensidad en puntos diferentes a aquellos puntos donde si se conoce el valor Entre otras técnicas, se destacan los métodos de re-sampling.

De este modo, se emplean diferentes criterios para determinar los valores $V_{O}(k, l)$ para pixels $(k, l)$ donde el input $V_{I}$ no es conocido:

Interpolación al vecino más cercano.
Interpolación bilineal.
Interpolación bicúbica.

La técnica de interpolacoón al vecino más cercano (Nearest neighbor interpolation) está basada en superponer el arreglo 2D output al arreglo 2D input calculando el valor para los pixels $(k, l)$ según los valores conocidos $V_{I}(i, j)$, utilizando un promedio (que puede cuantificarse de diferentes maneras) de los vecinos más cercanos equidistantes. Sin embargo, puede verse que esta técnica presenta algunos efectos indeseables.

La tácnica de interpolación lineal considera los 4 pixels más cercanos a $V(k, l)$ para la interpolación. Se realiza un promedio entre estos 4 valores para determinar el valor desconocido del pixel $(k, l)$. La imagen output resulta más “suave” que para el caso de la técnica Nearest neighbor interpolation. Pero, puede causar que la imagen se vea algo “difusa”.

Entonces, los valores de pixels $(k, l)$, para los cuales no se conoce $V_{I}(k, l)$ se obtienen a partir de:

\[\begin{split}\begin{aligned} V_{O}(k, l) = (1 - \alpha)\, (1-\beta) \, V_{I}(i,j) + \alpha (1 - \beta) \, V_{I}(i +1, j) + \nonumber \\ (\alpha -1) \, V_{I}(i, j+1) + \alpha \, \beta \, V_{I}(i +1, j +1) \label{EqXXIX}\end{aligned}\end{split}\]

donde $\alpha \equiv k - i$, $\beta \equiv l -j$, $i \equiv floor(k)$ y $j \equiv floor(l)$ [3].

Por su parte, la técnica de interpolación bicúbica Es el algoritmo de interpolación más utilizado. Considera los 16 pixels más cercanos a cada pixel $(k, l)$ cuyo valor debe determinarse por interpolación. Se aproxima localmente al valor (el nivel de gris) en la imagen original mediante una superficie polinómica de tipo bicúbica. Resulta ser, de las técnicas quí descritas, el óptimo al considerar el balance entre tiempo de cómputo y performance.

La implementación de este método puede llevarse a cabo por medio de procesar el bloque $B(k, l)$, centraado en el pixel $(k, l)$, cuyas dimensiones se corresponden con las dimensiones de la máscara (16 pixels en un arreglo 5 $\times$ 5):

\[\begin{split}\begin{aligned} B(k, l) = \sum _{i=0}^{3} \sum _{j=0}^{3} \, q^{(k, l)}_{i, j} (k - k')^{i} \, (l - l')^{j} \\ \nonumber \, \, \; \; k', \, \in [k - 2, k + 2] \; \, \& \; l' \, \in [l - 2, l + 2] \label{EqXXX}\end{aligned}\end{split}\]

donde los coeficientes $q_{i, j}$ deben ser determinados. O bien,

\[\begin{aligned} V_{O}(k, l) = h(k) \, h(l) \label{EqXXXI}\end{aligned}\]

donde la función de interpolación $h$ se define, a trozos, del siguiente modo:

\[\begin{split}\begin{aligned} h(p) \equiv 1 - \, \lvert p \rvert^{2} + \lvert p \rvert^{3} \; \, \; \forall \lvert p \rvert < 1 \nonumber \\ h(p) \equiv 4 - \, 8 \, \lvert p \rvert^{2} + 5 \, \lvert p \rvert^{2} - \lvert p \rvert^{3} \; \, \; \forall 1 \leq \lvert p \rvert < 2 \\ h(p) \equiv 0 \, \; \, \forall p \geq 2 \nonumber \label{EqXXXII}\end{aligned}\end{split}\]

Comparación cualitativa de performance de algoritmos de interpolación¶

Interpolación de vecino más cercano: El error de posición resulta, a los sumo, medio pixel, que es perceptible en objetos con fronteras rectas en las que aparece un efecto de salto después de de esta transformación.
Interpolación Lineal: Genera una leve disminución de resolución debido al borroneo (blurring) intrínseco al modo de cálculo del valor promedio, pero disminuye el efecto de salto que presenta el algoritmo de vecino más cercano.
Interpolación Bicúbica: No presenta el problema del efecto de salto a la vez que genera un menor blurring.

Relaciones básicas entre pixels¶

La relación básica más inmediata entre pixels es la distancia $D$ entre dos pixels $(m, n)$ y $(m', n')$.

Los axiomas para definir una métrica o función de distancia entre pixels $D$ requieren de los siguientes criterios:

$D(k \; k', l \; l') \geq 0$ con $D(k \; k', l \; l') = 0 \Leftrightarrow k=k' \, \; l=l'$
$D(k \; k', l \; l') = D(k' \; k, l' \; l)$
$D(k \; k', l \; l') \leq D(k \; k', s \; s') + D(s \; s', l \; l')$

A partir de estas condiciones pueden definirse diferentes métricas. Entre ellas:

\[\begin{aligned} D(k \; k', l \; l') \equiv \sqrt{\left( k - k' \right)^2 + \left( l - l' \right)^2} \label{EqXXXIII}\end{aligned}\]

\[\begin{aligned} D_{4}(k \; k', l \; l') \equiv \lvert k - k' \rvert + \lvert l - l' \rvert \label{EqXXXIV}\end{aligned}\]

\[\begin{aligned} D_{8}(k \; k', l \; l') \equiv \max \left( \lvert k - k' \rvert , \lvert l - l' \rvert \right) \label{EqXXXIV}\end{aligned}\]

Las definiciones Euclidea, $D_{4}$ y $D_{8}$ para la distancia entre pixels no depende de adyacencias sino exclusivamente de las coordenadas espaciales $(k, l)$.

Puede verse, a partir de las definiciones de las métricas que la condición $D(k \, k', l \, l') \leq. R$ determina un círculo centrado en $(k, l)$ para la métrica Euclidea, un rombo para la métrica $D_{4}$ y un cuadrado para la métrica $D_{8}$.

Operadores sobre imágenes¶

Para operar sobre imágenes pueden utilizarse herramientas basadas en operaciones matriciales de álgebra lineal y operaciones “de array” orientadas pixel a pixels. $\mathbf{H}$ es un operador arbitrario sobre una imagen cuya representación matricial es $f(m, n)$ si satisface:

\[\begin{aligned} \mathbf{H} \left[ f(m, n) \right] = g(m, n) \label{EqXXXV}\end{aligned}\]

Además, $\mathbf{H}$ es un operador lineal si:

\[\begin{aligned} \mathbf{H} \left[ \sum _{j} \alpha_{j} f_{j}(m, n) \right] = \sum _{j} \alpha_{j} \; \mathbf{H} \left[ f_{j}(m, n) \right] \label{EqXXXVI}\end{aligned}\]

Una aplicación importante de las propiedades de linealidad de operadores sobre imágenes es la descripción de imágenes $g(m, n)$ como contribución “original” ($f(m, n)$) y ruido random ($r(m, n)$):

\[\begin{aligned} g(m, n) = f(m, n) + r(m, n) \label{EqXXXVII}\end{aligned}\]

La imagen de ruido es de tipo random si los valores de pixels de $r(m, n)$ son aleatorios no correlacionados y con esperanza 0.

Promediando $N_{Tot}$ imágenes con ruido random se obtiene la imagen promedio $\langle g \rangle$ dada por:

\[\begin{aligned} \langle g \rangle (m, n) = \frac{1}{N_{Tot}} \sum _{j=1} ^{N_{Tot}} g_{j} (m, n) \label{EqXXXVIII}\end{aligned}\]

La aplicación del teorema del límite central establece que la imagen promedio $\langle g \rangle (m, n) \; \rightarrow f(m, n)$ (imagen “original”) para $N_{Tot} \rightarrow \infty$.

Otra aplicación útil de los operadores lineales es la substracción de una máscara [4] $M(m, n)$ a la imagen original $f(m, n)$:

\[\begin{aligned} g (m, n) = f(m, n) - M(m, n) \label{EqXXXIX}\end{aligned}\]

Adición y diferencia de imágenes¶

Para ejemplificar las operaciones, se utilizan imágenes 8-bits.

Por tanto, los valores de la imagen resultado de la adición de dos imágenes varían en $[0, 510]$. Mientras que los valores de la imagen resultado de la diferencia de dos imágenes varían en $[-255, 255]$.

La adecuación ($f_{A}$) de los valores de la imagen resultado de adición/diferencia de dos imágenes se realiza del siguiente modo:

\[\begin{aligned} f_{A} (m, n) = round \left[ \left( 2^{N} - 1 \right) \frac{f(m, n) - min{ \left[ f(m, n) \right] }}{max{ \left[ f(m, n) - min{f(m, n)} \right] }} \right] \label{EqXL}\end{aligned}\]

Para imágenes de tipo $N$-bits.

Operaciones sobre pixels¶

La introducción de operaciones espaciales que se llevan a cabo sobre los valores de pixels de la imagen permiten:

Operaciones de un pixel.
Operaciones de vecindad.
Transformaciones geométricas.

Operaciones de un pixel

Se modifica el valor de un pixel de modo individual en la imagen original $f(m, n)$, dando como resultado $g(m, n)$ dado por:

\[\begin{aligned} g (m, n) = \mathbf{T} \left( f(m, n) \right) \label{EqXLI}\end{aligned}\]

de manera que el valor de imagen es modificado por la transformación $\mathbf{T}$. Este concepto se aplica, por ejemplo, para determinar “el negativo”

Operaciones de vecindad

Sea $C (M, N)$ un conjunto de pixels ($M := [m_{min}, m_{max}]$ y $N := [n_{min}, n_{max}]$) entorno (vecinos) al pixel $(m, n)$.

A partir de este tipo de operaciones de vecinos puede calcularse, por ejemplo, el valor medio en un entorno rectangular ($M \times N$) de un pixel de interés [5]. Resulta:

\[\begin{aligned} g (m, n) = \frac{1}{ M \; N} \sum _{(i, j) \in C(M, N)} f(i, j) \label{EqXLII}\end{aligned}\]

Transformaciones geométricas.

Las transformaciones geométricas $\mathbf{T}$ de una image $f(m, n)$ puede obtenerse a partir de una transformación de índole geométrico de coordenadas espaciales: al valor del pixel $(m, n)$ se asigna el valor de un pixel $(i, j)$.

Debido a la naturaleza discreta de la representación de imágenes, debe considerarse el proceso de interpolación para obtener los valores de pixels como resultado de aplicar l transformación $\mathbf{T}$.

Una de las categorías principales de los operadores de transformación son las transformaciones denominadas afines, que incluyen translaciones, rotaciones, escalados, reflexiones y proyecciones, entre otros.

Algunos ejemplos de operadores de transformación son:

Rotación: $\mathbf{T_{Rot}} = \begin{array}{cc} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \\ \end{array}$
Escaleo: $\mathbf{T_{Esc}} = \begin{array}{cc} e_{i} & 0 \\ 0 & e_{j} \\ \end{array}$
Traslación: $\mathbf{T_{Tra}} = \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ t_{i} & t_{j} & 0 \\ \end{array}$

Transformadas dicretas: La transformada de Fourier¶

Desde un punto de vista general, las transformadas constituyen operaciones espaciales sobre una imagen original $f(m, n)$, representada en el dominio espacial (que se refiere a las coordenadas $(m, n)$) y una imagen resultado $F(m, n)$ que procesan los valores de pixels en el plano geométrico.

Existen diferentes modos de representar de la imagen, en términos del espacio ce representación:

la imagen $f(m, n)$ es representada por una matriz $M \times N$ de pixels $(m, n)$ discretos.
la imagen $F(m*, n*)$ es representada por una matriz $M \times N$ de variables transformadas $(m*, n*)$.

Como se introdujo de modo cualitativo ([EqXXV] y [EqXXVI]), una transformación lineal de una imagen original $f(m, n)$ significa‘:

\[\begin{aligned} F (m*, n*) = \sum _{m} \sum _{n} f(m, n) \, k(m \; m*, n \; n*) \label{EqXLIII}\end{aligned}\]

donde $k$ es el kernel de la transformación.

La transformada directa (fordward) de $f(m, n)$ deviene en $F(m*, n*)$, y la transformada inversa (inverse) de $F(m*, n*)$ deviene en $f(m, n)$. Por tanto, el equivalente a la expresión ([EqXLIII]) es:

\[\begin{aligned} f (m, n) = \sum _{m*} \sum _{n*} F(m*, n*) \, k(m* \; m, n* \; n) \label{EqXLIV}\end{aligned}\]

donde $k(m* \; m, n* \; n)$ es el kernel de la transformación inversa.

De este modo, se habilita la posibilidad de operar en el espacio de la transformada. Es decir:

\[\begin{aligned} f (m, n) \; \underrightarrow{\mathbf{T}} \; \; F(m*, n*) \; \underrightarrow{\mathbf{O}} \; \; G(m*, n*) \; \underrightarrow{\mathbf{T^{-1}}} \; \; g(m, n) \label{EqXLV}\end{aligned}\]

donde $\mathbf{T}$ y $\mathbf{T^{-1}}$ representan la transformada directa e inversa, respectivamente. $\mathbf{O}$ es un operador arbitrario.

Resulta de particular importancia la propiedad de los kernels de ser separable en variables. Es decir:

\[\begin{aligned} k (m \; m*, n \; n*) = k_{(m, n)} (m, n) \; k_{(m*, n*)} (m*, n*) \label{EqXLVI}\end{aligned}\]

La transformada discreta de Fourier bidimensional 2D se define a partir de los kernels de transformación:

\[\begin{split}\begin{aligned} k_{TF} (m \; m*, n \; n*) = e^{-2 \pi i \left( \frac{m \, m*}{M} + \frac{n \, n*}{N}\right)} \nonumber \\ k_{(TF)^{-1}} (m \; m*, n \; n*) = \frac{1}{M \, N}e^{2 \pi i \left( \frac{m \, m*}{M} + \frac{n \, n*}{N}\right)} \label{EqXLVII}\end{aligned}\end{split}\]

Por tanto, la operación de transformadas discretas directa ($\mathbf{TF}$) e inversa ($\mathbf{(TF)^{-1}}$) resultan:

\[\begin{split}\begin{aligned} F(m*, n*) = \sum _{m} ^{M-1} \sum _{n} ^{N-1} f(m, n) \; e^{-2 \pi i \left( \frac{m \, m*}{M} + \frac{n \, n*}{N}\right)} \nonumber \\ f(m, n) = \frac{1}{M \, N} \sum _{m*} ^{M-1} \sum _{n*} ^{N-1} F(m*, n*) \; e^{2 \pi i \left( \frac{m \, m*}{M} + \frac{n \, n*}{N}\right)} \label{EqXLVIII}\end{aligned}\end{split}\]

Cuyo análogo en espacios continuos es:

\[\begin{split}\begin{aligned} F(u, v) = \mathbf{TF}[f(x, y)] = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) \; e^{-2 \pi \i (u \, x + v \, y)} \; dx dy \nonumber \\ f(x, y) = \mathbf{(TF)^{-1}}[F(u, v)] = \frac{1}{4 \pi^{2}} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(u, v) \; e^{2 \pi i (u \, x + v \, y)} \; du dv \label{EqLI}\end{aligned}\end{split}\]

La expresión ([EqXLIX]) para la transformada de Fourier puede interpretarse, dejando de lado momentaneamente problemas de existencia y unicidad, como una suma de exponenciales complejas con pesos para los términos, donde las variables $m*$ y $n*$ representan las frecuencias en el dominio de la transformada.

El valor de la transformada en $(m*, n*)$ ($F(m*, n*)$) contribuye a través de $F(m*, n*) \, e^{2 \pi i (u \, x + v \, y)}$ y puede verse, ya que $f(m, n)$ es una función real, que $F(m*, n*) = F^{\prime} (m*, n*)$, donde $\prime$ indica el complejo conjugado.

A modo de ejemplo, la figuras [Fig2_3], [Fig2_4] y [Fig2_5] presentan resultados de aplicar la transformada de Fourier de la imagen orifinal $f(m, n)$ para diferentes casos.

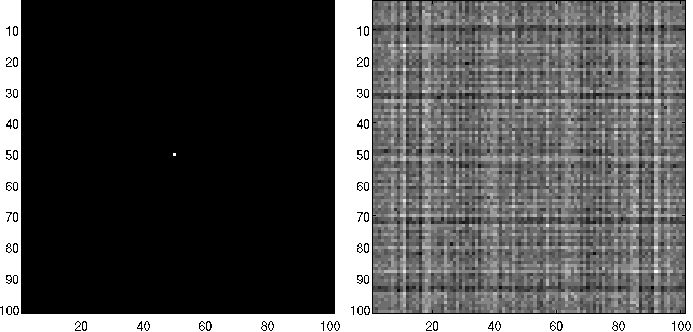
Figura 4: Ejemplo de transformada de Fourier: $f(m, n) = 0$; $\forall (m, n) \neq (51, 51)$; $m, n \in [1, 101]$ obtenido con plataforma MatLab [*].

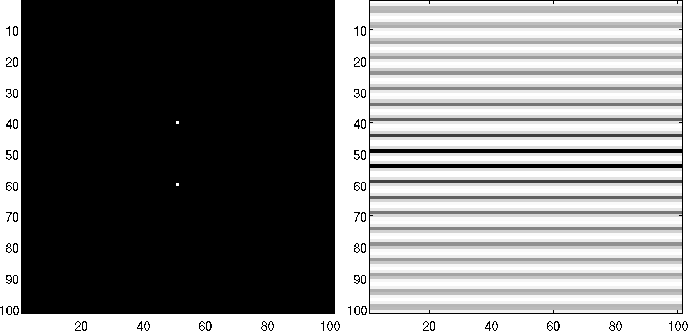
Figura 5: Ejemplo de transformada de Fourier: $f(m, n) = 0$; $\forall (m, n) \neq (40, 51)$, $\vee \neq (60, 51)$; $m, n \in [1, 101]$ obtenido con plataforma MatLab.

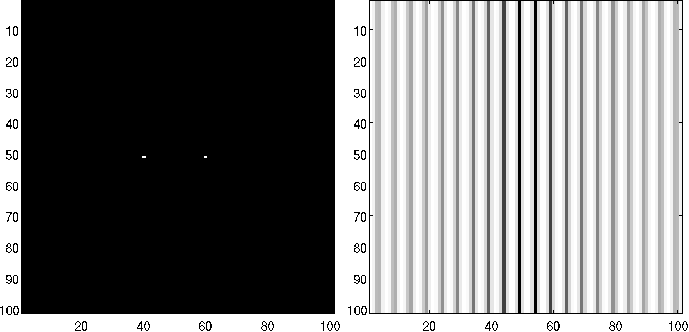
Figura 6: Ejemplo de transformada de Fourier: $f(m, n) = 0$; $\forall (m, n) \neq (51, 40)$, $\vee \neq (51, 60)$; $m,n \in [1, 101]$ obtenido con plataforma MatLab.

Filtros¶

A partir de las definiciones introducidas por las expresiones ([EqL]) y ([EqLI]) resulta posible realizar procesos de filtrado tanto en el dominio especial de la imagen original $f(m, n)$ como en el dominio de las frecuencias de la transformada $F(m*, n*)$.

Una característica significativa, que representa de hecho una de las principales ventajas de los espacios de transformadas, es que la operación de filtrado se realiza por medio de una multiplicación de transformadas; mientras que la operación en el espacio de coordenadas significa una convolución denotada por el símbolo $\otimes$. En virtud del teorema de convolución, se tiene:

\[\begin{aligned} f(m, n) \otimes g(m, n) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(m, n) \; g(m-k, n-l)\; dk \, dl \label{EqLII}\end{aligned}\]

Aplicando la definición de transformada de Fourier, se obtiene:

\[\begin{split}\begin{aligned} F_{f, g}(m*, n*) \equiv \mathbf{TF} [ f(m, n) \otimes g(m, n) ] = \nonumber \\ \mathbf{TF} [ f(m, n)] \; \mathbf{TF} [ g(m, n)] = F(m*, n*) \; G(m*, n*) \label{EqLIII}\end{aligned}\end{split}\]

Para una dada función original $f(m, n)$ y su correspondiente transformada de Fourier $F(m*, n*)$, en referencia a la expresión ([EqLIII]) el operador $G(m*, n*)$ se define como un filtro espacial lineal o función de transferencia de filtro.

Entonces, la imagen resultado del proceso de filtrado $h(m, n)$ se obtiene aplicando la transformada inversa:

\[\begin{aligned} h(m, n) = \mathbf{TF^{-1}} [F_{f, g}(m*, n*) ] \label{EqLIV}\end{aligned}\]

El filtro queda determinado por medio de la función de transferencia o bien por la respuesta de impulso $j(m, n)$ definida a partir de:

\[\begin{split}\begin{aligned} j(m, n) = F_{f, g}(m, n) = \delta (m, n) \otimes j(m, n) = \nonumber \\ \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(m, n) \, j(k-m, l-n) \; dk \, dl \label{EqLV}\end{aligned}\end{split}\]

Resulta que $j(m, n)$ es un filtrado intenso en términos de la función $\delta$ de Dirac.

A fines de cómputo, la transformada discreta de Fourier puede obtenerse, en modo análogo a la expresión ([EqXLVIII]) operando:

\[\begin{split}\begin{aligned} F(m^*, n^*) = \mathbf{TF}[f(m, n)] = \frac{1}{M \, N} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(m, n) \; \nonumber \\ \left[ \cos \left( 2 \pi (\frac{m^* \, m}{M} + \frac{n^* \, n}{N}) \right) + i \, \sin \left( 2 \pi (\frac{m^* \, m}{M} + \frac{n^* \, n}{N}) \right)\right] \nonumber \\ f(m, n) = \mathbf{TF^{-1}} [F(m^*, n^*)] = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} F(m^*, n^*) \; \nonumber \\ \left[ \cos \left( -2 \pi (\frac{m^* \, m}{M} + \frac{n^* \, n}{N}) \right) - i \, \sin \left( 2 \pi (\frac{m^* \, m}{M} + \frac{n^* \, n}{N}) \right)\right] \nonumber \\ \label{EqLVI}\end{aligned}\end{split}\]

Debido a la naturaleza discreta del espacio de muestreo intrínseco al procesamiento digital de imágenes, se determina la relación entre dominios espaciales y de frecuencias por medio de:

\[\begin{split}\begin{aligned} \Delta m^* = \frac{1}{M\; \Delta m} \\ \Delta n^* = \frac{1}{N\; \Delta n} \label{EqLVII}\end{aligned}\end{split}\]

Cabe destacar que, por conveniencia de procesamiento, para el caso de imágenes “cuadradas” para las que $N = M$, se redefine la expresión para la transformada de Fourier, multuplicando la expresión ([EqLVI]) por $N$, es decir:

\[\begin{split}\begin{aligned} F(m^*, n^*) = \mathbf{TF}[f(m, n)] = \frac{1}{N} \sum_{m=0}^{N-1} \sum_{n=0}^{N-1} f(m, n) \; e^{-2 \pi \, i \, \left( \frac{m^* \, m + n^* \, n}{N} \right)} \nonumber \\ f(m, n) = \mathbf{TF^{-1}} [F(m^*, n^*)] = \frac{1}{N} \sum_{m=0}^{N-1} \sum_{n=0}^{N-1} F(m^*, n^*) \; e^{2 \pi \, i \, \left( \frac{m^* \, m + n^* \, n}{N} \right)} \nonumber \\ \label{EqLVIII}\end{aligned}\end{split}\]

La componente espectral compleja de $F(m^*, n^*)$ determina módulo y fase, respectivamente, dados por:

\[\begin{split}\begin{aligned} \lvert F(m^*, n^*) \rvert = \sqrt{\left[ \Re{ \left( F(m^*, n^*) \right) }\right]^{2} + \left[ \Im{\left( F(m^*, n^*) \right) } \right]^{2}} \nonumber \\ \phi(m^*, n^*) = \arctan \left[ \frac{\Im{\left( F(m^*, n^*) \right) }}{\Re{\left( F(m^*, n^*) \right) }}\right] \label{EqLIX}\end{aligned}\end{split}\]

donde $\Im$ y $\Re$ representan las componentes imaginaria y real, respectivamente. Al filtrar una imagen original cuadrada $f(m, n)$ de dimensiones $N \times N$ mediante un filtro $j(m, n)$ de dimensiones $L \times L$ se obtendrá una imagen resultado $g(m, n)$ de dimensiones $N + L -1 \; \; \times \; \; N + L -1$.

Las propiedades de la transformada de Fourier permiten identificar de modo sencillo los operadores más relevantes del procesamiento digital, como:

\[\begin{split}\begin{aligned} f(m, n)e^{2 \pi \, i (\frac{m^* _{0} \, m + n^* _{0} \, n}{N})} \leftrightarrow F(m^* - m^* _{0}, n^* - n^* _{0}) \\ f(m - m_{0}, n - n_{0}) \leftrightarrow F(m^*, n^*) \, e^{-2 \pi \, i (\frac{m^* \, m_{0} + n^* \, n_{0}}{N})} \nonumber \label{EqLX}\end{aligned}\end{split}\]

Es decir, una traslación al punto $(m_{0}, n_{0})$ se identifica con con el corrimiento del origen del plano del dominio de frecuencias al punto $(m^*_{0}, n^*_{0})$.

En coordenadas polares $m = \rho \, \cos{\theta} \; \; n = \rho \, \sin{\theta} \; \; m^* = \omega \, \cos{\phi} \; \; n^* = \omega \, \sin{\phi}$, las imágenes original $f(m, n)$ y transformada $F(m^*, n^*)$ son expresadas como $f(\rho, \theta)$ y $F(\omega, \phi)$.

Aplicando la definición de transformada de Fourier, resulta:

\[\begin{aligned} f(\rho, \theta + \theta_{0}) \leftrightarrow F(\omega, \phi + \theta_{0}) \label{EqLXI}\end{aligned}\]

Es decir, la rotación de la imagen original $f(\rho, \theta)$ (o $f(m, n)$) por un ángulo $\theta_{0}$ se vincula con una rotación del mismo ángulo en la imagen resultante $F(\omega, \phi)$ (o $F(m^*, n^*)$).

Las figuras [Fig2_6] y [Fig2_7] muestran ejemplos de aplicación de operadores de rotación, en dominio de coordenadas y de frecuencias, respectivamente.

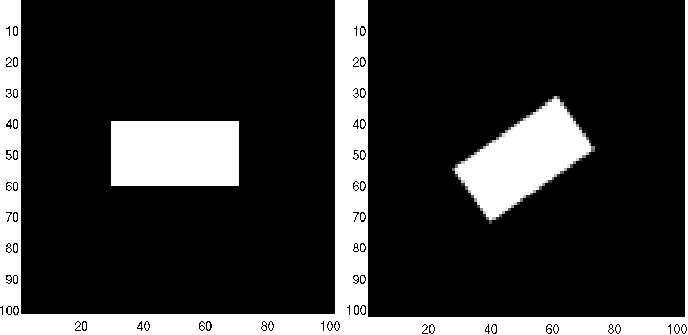
Figura 7: Rotación de $35^{\deg}$ de una imagen original $f(m, n)$ (o $f(\rho, \theta)$) obtenido con plataforma MatLab.

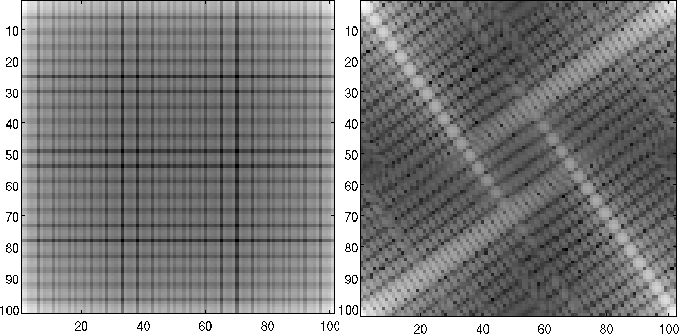
Figura 8: Rotación de $35^{\deg}$ de una imagen en dominio de transformada $F(m^*, n^*)$ (o $F(\omega, \phi)$) obtenido con plataforma MatLab.

Operador de Escaleo

La definición de transformada de Fourier implica que $\mathbf{TF} [f_{A}(m, n) + f_{B}(m, n)] = \mathbf{TF} [f_{A}(m, n)] + \mathbf{TF}[f_{B}(m, n)]$ pero $\mathbf{TF} [f_{A}(m, n) \cdot f_{B}(m, n)] \neq \mathbf{TF} [f_{A}(m, n)] \cdot \mathbf{TF}[f_{B}(m, n)]$.

Sin embargo, para escalares $\alpha$ y $\beta$ se tiene:

\[\begin{split}\begin{aligned} \alpha \, f(m, n) \leftrightarrow \alpha \, F(m^*, n^*) \\ f(\alpha m, \beta n) = \frac{1}{\lvert \alpha \beta \rvert} F(\alpha \, m^*, \beta \, n^*) \label{EqLXII}\end{aligned}\end{split}\]

Cálculo de promedios

El valor medio $\langle f \rangle$ se obtiene a partir de:

\[\begin{aligned} \langle f \rangle = \frac{1}{N^2} \sum _{m=0}^{N-1} \sum _{n=0}^{N-1} f(m, n) \label{EqLXIII}\end{aligned}\]

En particular, tomando $F(m^*=0, n^*=0)$ en la expresión ([EqLIX] (59)) se obtiene $F(0, 0)= \frac{1}{N} \sum _{m=0}^{N-1} \sum _{n=0}^{N-1} f(m, n)$. Por lo tanto, el valor promedio puede calcularse directamente a partir de:

\[\begin{aligned} \langle f \rangle = \frac{1}{N} F(m^* = 0, n^* = 0) \label{EqLXIV}\end{aligned}\]

Cálculo de operadores de derivadas: OPerador de Laplace

La laplaciana $\nabla^2$ de una imagen original $f(m, n)$ está dada por:

\[\begin{aligned} \nabla^2 f(m, n) \equiv \frac{\partial^2}{\partial m^2} + \frac{\partial^2}{\partial n^2} \label{EqLXV}\end{aligned}\]

Aplicando la definición de transformada de Fourier, se obtiene una expresión útil para el cálculo de la Laplaciana:

\[\begin{aligned} \mathbf{TF}[ \nabla^2 f(m, n) ] = -(2 \pi)^2 \left[ (m^*) ^2 + (n^*) ^2 \right] \; F(m^*, n^*) \label{EqLXVI}\end{aligned}\]

Filtros de paso de banda¶

Las transiciones abruptas, como bordes y contornos, en una imagen original $f(m, n)$ se corresponden con altas frecuencias en el dominio de la transformada.

Filtros de suavizado¶

Puede aprovecharse esta característica para implementar métodos de filtrado para suavizar operando en el dominio de frecuencias.

Es posible suprimir frecuencias por debajo o por encima de valores pre determinados de manera que se produzcan efectos de suavizado según requerimientos.

Filtros ideal de paso alto

Consiste en la utilización de la expresión ([EqLIII]) con la función de transferencia $G_{P,A}(m^*, n^*)$ definida por:

\[\begin{split}\begin{aligned} G_{P,A}(m^*, n^*) = \left\{ \begin{array}{ll} 0 & \mbox{$D(m^*, n^*) \leq D_{max}$}\\ 1 & \mbox{$D(m^*, n^*) > D_{max}$}.\end{array} \right. \label{EqLXVII}\end{aligned}\end{split}\]

Para un valor máximo de distancia $D_{max}$ como umbral para la distancia (independientemente de la métrica), $D(m^*, n^*)$ es la distancia al origen de frecuencias $(m^* = 0, n^* = 0)$.

En el caso de la métrica Euclidea $D(m^*, n^*) = \sqrt{ (m^*)^2 + (n^*)^2}$, el filtro se representa por un círculo de radio $D_{max}$ como muestra la figura [Fig2_8].

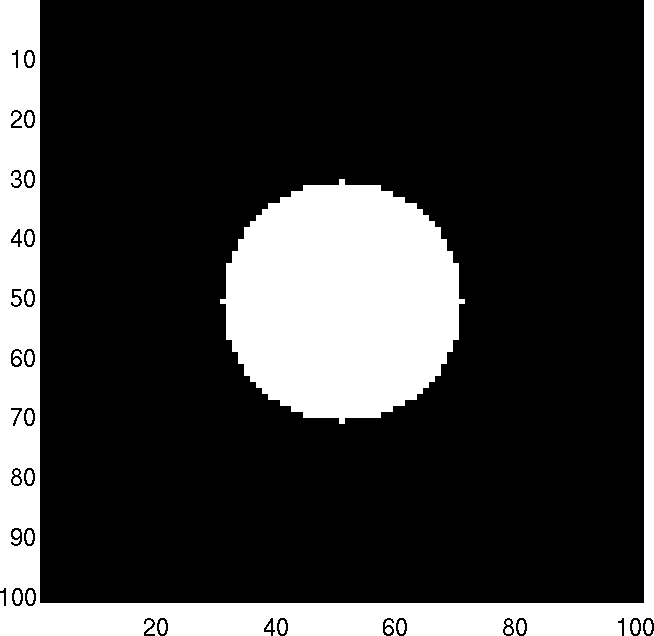
Figura 9: Matriz de transferencia $G_{P\,A}$ para un filtro ideal de paso alto obtenida con plataforma MatLab.

Filtros ideal de paso bajo

De modo análogo, para el caso del filtro de paso bajo se define a partir de la matriz de transferencia $G_{P,B}$ dada por:

\[\begin{split}\begin{aligned} G_{P,B}(m^*, n^*) = \left\{ \begin{array}{ll} 1 & \mbox{$D(m^*, n^*) \leq D_{max}$}\\ 0 & \mbox{$D(m^*, n^*) > D_{max}$}.\end{array} \right. \label{EqLXVIII}\end{aligned}\end{split}\]

La figura [Fig2_9] muestra la matriz de transferencia de paso bajo $G_{P\,B}$.

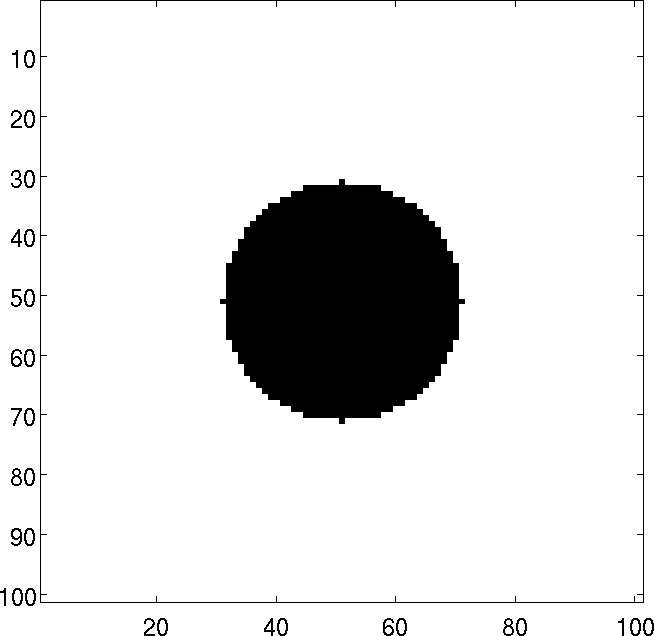
Figura 10: Matriz de transferencia $G_{P\,B}$ para un filtro ideal de paso alto obtenida con plataforma MatLab.

Máscaras para filtrado¶

Una máscara de filtrado $h(m, n)$ se denomina máscara de convolución espacial si se define pormedio de:

\[\begin{aligned} F(m^*, n^*) = \frac{1}{N} \sum _{m=0}^{N-1} \sum _{m=0}^{N-1} h(m, n) \, e^{-2 \pi i \left( \frac{m^* \, m + n^* \, n}{N} \right)} \label{EqLXIX}\end{aligned}\]

Si la máscara se restringue a una región específica, tal que $h(m, n) = 0$ para $m \wedge n \ge N_{max} < N$ de modo que la máscara restringida sea designada por $\hat{h}$, se obtiene:

\[\begin{aligned} \hat{H}(m^*, n^*) = \frac{1}{N} \sum _{n=0}^{N_{max}-1} \sum _{m=0}^{N_{max}-1} \hat{h}(m, n) \, e^{-2 \pi i \left( \frac{m^* \, m + n^* \, n}{N} \right)} \label{EqLXX}\end{aligned}\]

De modo que puedan determinarse los coeficientes de la expansión en ([EqLXX]) que de minimizar la cantidad:

\[\begin{aligned} \chi^2 \equiv \sum _{m^*=0}^{N-1} \sum _{n^*=0}^{N-1} \lvert \hat{H}(m^*, n^*) - H(m^*, n^*) \rvert^2 \label{EqLXXI}\end{aligned}\]

La expresión anterior ([EqLXXI]) puede resolverse por medio de una representación algebraica lineal $\mathbf{\hat{H}} = \mathbf{Q} \, \mathbf{\hat{h}}$ con $\mathbf{\hat{H}}$ representado por un vector de dimensión $N^2$ cuyos elementos son los de $\hat{H}$ ordenados de algún modo arbitrario, $\mathbf{\hat{h}}$ es un vector columna de dimensiones $N_{max}^2$ conteniendo los elementos de $\hat{h}$ y $\mathbf{Q}$ es una matriz de dimensiones $N^2 \times N_{max}^2$ de términos exponenciales de acuerdo con la expresión ([EqLXIX]) dados por:

\[\begin{aligned} \mathbf{Q}(k, l) = q(k, l) = \frac{1}{N} e^{-2 \pi i \left( \frac{m^* \, m + n^* \, n}{N} \right)} \label{EqLXXII}\end{aligned}\]

para $k= m^* N + n^*$ con $m^* \wedge n^* \in [0, N-1]$ y $l= m N_{max} + n$ con $m \wedge n \in [0, N_{max}-1]$.

[1]

Se entiende como rayos X a aquellos producidos en interacciones atómicas, y rayos $\gamma$ a aquellos producidos por interacciones internucleares. No existe a priori diferencia energética entre ellos y ambos son constituidos por fotones, la diferencia se realiza a partir de su procedencia. En adelante se utilizará indistintamente las letras X o $\gamma$ para referirse a fotones.

[2]	Este parámetro es denominado “umbral” y su valor condiciona la performance de la técnica.

[3]	Aquí la función floor se define por medio de asignar al argumento el número entero más grande que sea menor que el argumento.

[4]	Un ejemplo típico son las imágenes médicas por contraste, como angiografías.

[5]	Este método resulta de utilidad para suprimir detalles o realzar regiones.

[*]	Official license MathWorks 3407-8985-4332-9223-7918.