Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Introducción a la Física
Guía N 3
3
Problema 1:
La función de movimiento de un cuerpo que se desplaza sobre una
recta es:
donde ![$[x]$](img3.gif) son centímetros y
son centímetros y ![$[t]$](img4.gif) segundos.
segundos.
a) Calcular la velocidad media del móvil en los
intervalos de tiempo (en segundos): [0, 1] y [0, 4].
b) Calcular la velocidad media del móvil para el
intervalo [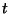 ,
, 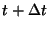 ].
].
c) ¿A qué valor tiende esta expresión cuando
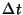 es muy pequeño?
es muy pequeño?
d) Encuentre él o los puntos en los que el cuerpo
está en reposo.
e) Obtenga la expresión general de la aceleración
del cuerpo.
f) Grafique la posición, velocidad y aceleración
del cuerpo en función del tiempo.
Problema 2:
Cada uno de los siguientes cambios de velocidad, tienen lugar en un
intervalo de tiempo de 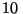 s. Calcule para cada intervalo la
aceleración media.
s. Calcule para cada intervalo la
aceleración media.
a) Al comienzo del intervalo, un cuerpo se mueve
hacia la derecha sobre el eje x a la velocidad de
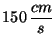 ; al final del intervalo se mueve hacia
la derecha a la velocidad de
; al final del intervalo se mueve hacia
la derecha a la velocidad de
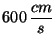 .
.
b) Al comienzo del intervalo se mueve hacia la
derecha a
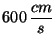 y al final hacia la
derecha a la velocidad de
y al final hacia la
derecha a la velocidad de
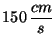 .
.
c) Al comienzo se mueve hacia la derecha a
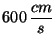 y al final hacia la izquierda a
y al final hacia la izquierda a
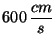 .
.
d) Al comienzo se mueve hacia la izquierda a
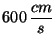 y al final hacia la izquierda a
y al final hacia la izquierda a
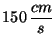 .
.
Problema 3:
Una partícula se desplaza a lo largo del eje x de acuerdo a la
ley
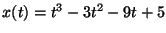 .
.
a) ¿Durante qué intervalos de tiempo la
partícula se está moviendo en la dirección positiva
del eje x?
b) ¿Durante qué intervalos se está moviendo
en la dirección negativa del eje x?
c) ¿Durante qué intervalos de tiempo el movimiento
es acelerado y en cuáles es retardado?
d) Grafique 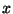 ,
, 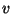 y
y 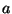 en función del tiempo.
en función del tiempo.
Problema 4:
Las ecuaciones de movimiento de tres cuerpos que se mueven sobre un
camino unidimensional son:
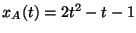 ,
,
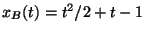 y
y
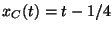 .
.
a) Calcule analítica y gráficamente él o los
puntos de encuentro de los cuerpos 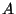 ,
, 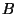 y
y 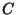 .
.
b) Calcule los instantes en que se producen dichos
encuentros.
c) Indique los instantes para los cuales las
velocidades de cada cuerpo se anulan.
d) ¿Cuál es la expresión para la aceleración
de cada uno de los cuerpos? Grafique 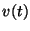 y
y 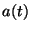 para cada uno
de los cuerpos.
para cada uno
de los cuerpos.
Problema 5:
Un móvil 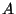 cuya función de movimiento es
cuya función de movimiento es 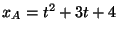 se
encuentra en el instante
se
encuentra en el instante 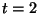 s con un móvil
s con un móvil 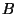 cuya función
de movimiento es
cuya función
de movimiento es 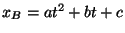 . Sabiendo que en
. Sabiendo que en 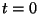 s el
móvil
s el
móvil 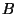 se encuentra 4 metros más lejos del origen que
se encuentra 4 metros más lejos del origen que 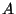 , y
que en
, y
que en 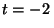 s su velocidad se anula; determine la función de
movimiento del móvil
s su velocidad se anula; determine la función de
movimiento del móvil 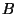 . ¿Existe otra solución?
. ¿Existe otra solución?
Problema 6:
Un movimiento uniformemente acelerado está dado por una expresión
del tipo
siendo 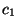 ,
, 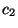 y
y 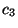 constantes.
Tomando:
constantes.
Tomando:
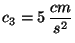 ;
y sabiendo que en
;
y sabiendo que en 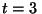 s,
s,
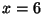 cm y que en
cm y que en 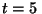 s,
s, 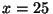 cm:
a) Encuentre la aceleración del movimiento
b) Calcule
cm:
a) Encuentre la aceleración del movimiento
b) Calcule 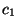 y
y 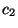 .
c) Interprete físicamente los coeficientes
.
c) Interprete físicamente los coeficientes
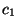 ,
, 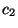 y
y 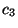 .
.
Problema 7:
La función posición de una partícula que se mueve sobre el
eje x depende del tiempo de la forma
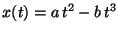 ,
donde
,
donde 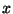 está en cm y
está en cm y 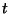 en s. ¿Qué unidades deben tener
en s. ¿Qué unidades deben tener 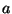 y
y
 ? Considerando
? Considerando 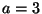 y
y 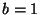 en las unidades adecuadas, calcule:
en las unidades adecuadas, calcule:
a) ¿En qué instante 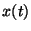 alcanza un valor
máximo como función del tiempo? ¿Es ese el máximo valor
posible de
alcanza un valor
máximo como función del tiempo? ¿Es ese el máximo valor
posible de 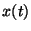 ?
?
b) Calcule el camino total recorrido en los
primeros 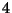 segundos.
segundos.
c) Calcule la velocidad y la aceleración de la
partícula para 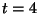 s. ¿Es un movimiento uniformemente
acelerado?
s. ¿Es un movimiento uniformemente
acelerado?
Problema 8:
La aceleración de un cuerpo en movimiento sobre el eje x está
dado por
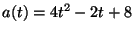 donde
donde
![$[a] = \displaystyle \frac{cm}{s^2}$](img45.gif) y
y ![$[t]=\,$](img46.gif) s.
Calcule una expresión general para la
velocidad, sabiendo que la misma es
s.
Calcule una expresión general para la
velocidad, sabiendo que la misma es
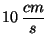 en
en 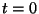 .
.
Problema 9:
La aceleración de un cuerpo que se mueve a lo largo de una
línea recta está dado por 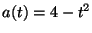 donde
donde 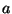 se da en
se da en
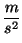 y
y 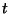 en segundos. Encontrar la
velocidad y la posición en función del tiempo suponiendo que
para
en segundos. Encontrar la
velocidad y la posición en función del tiempo suponiendo que
para 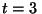 s,
s,
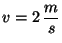 y
y 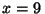 m.
m.
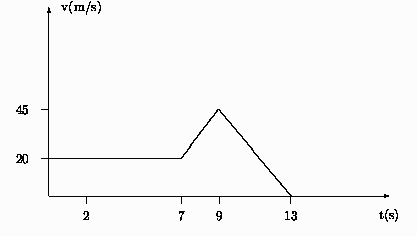
Problema 10:
La figura muestra la velocidad de un móvil en función de 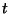 :
:
a) Determine la aceleración instantánea para
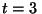 s y
s y 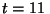 s.
s.
b) Calcule los caminos recorridos por el móvil
durante los primeros 5, 9 y 13 segundos.
c) Conociendo que 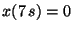 , encuentre la
posición del móvil en
, encuentre la
posición del móvil en 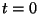 s.
s.
Problema 11:
La aceleración de una partícula es: 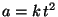
a) Sabiendo que
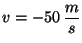 cuando
cuando 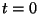 s y que
s y que
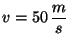 cuando
cuando
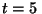 s, determine la constante
s, determine la constante 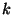 .
.
b) Escriba 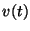 y
y 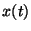 sabiendo que
sabiendo que 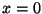 cuando
cuando
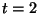 s.
s.
Problema 12:
Un cuerpo tiene una aceleración dada por 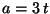 .
En
.
En 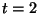 s el cuerpo se encuentra en
s el cuerpo se encuentra en 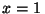 cm y en
cm y en 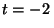 s
está en
s
está en 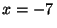 cm.
cm.
a) Calcule la velocidad y la posición del cuerpo en
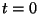 s.
s.
b) Calcule la velocidad del cuerpo en 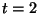 s y
s y
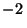 s.
s.
c) Haga un gráfico cualitativo de la función de
movimiento.
d) Grafique 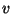 y
y 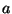 en función
en función 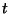
Problema 13:
Un tren parte de una estación con una aceleración constante de
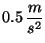 , hasta alcanzar una velocidad de
, hasta alcanzar una velocidad de
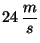 , que luego mantiene constante.
Calcular en que instantes la velocidad media es:
a)
, que luego mantiene constante.
Calcular en que instantes la velocidad media es:
a)
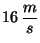 y
b)
y
b)
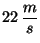 ;
y las caminos recorridos al cabo de dichos instantes.
;
y las caminos recorridos al cabo de dichos instantes.
Problema 14:
Un automóvil y un camión parten en el mismo instante,
encontrándose inicialmente el auto cierta distancia detrás
del camión. Este último tiene una aceleración constante de
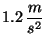 mientras que el auto acelera a
mientras que el auto acelera a
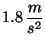 . El auto alcanza al camión
cuando éste ha recorrido
. El auto alcanza al camión
cuando éste ha recorrido 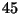 metros.
metros.
a) ¿Cuánto tiempo tarda el auto en alcanzar al
camión?
b) ¿Cuál es la distancia inicial entre ambos
vehículos?
c) ¿Cuál es la velocidad de cada uno en el momento
de encontrarse? Graficar 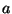 ,
, 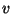 y
y 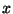 en función del tiempo.
en función del tiempo.
Problema 15:
Un móvil describe un movimiento armónico simple si su función
de movimiento 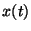 satisface la siguiente ecuación:
satisface la siguiente ecuación:
donde 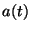 es la aceleración y
es la aceleración y 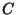 una constante
(
una constante
( ).
).
a) Pruebe que la función de movimiento:
satisface la ecuación del movimiento armónico simple
tomando 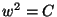 .
.
b) Encuentre los valores máximos y mínimos que
alcanza 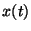 y los instantes de tiempo en los cuales ocurren.
y los instantes de tiempo en los cuales ocurren.
c) Interprete físicamente la constante 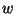 .
.
Problema 16:
Una partícula es acelerada en varios intervalos de tiempo
de acuerdo a:
a) Grafique 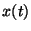 ,
, 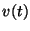 y
y 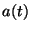 asumiendo que la
partícula se encontraba en reposo en el origen en
asumiendo que la
partícula se encontraba en reposo en el origen en 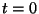 .
.
b) Calcule la velocidad de la partícula en
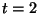 s y el camino recorrido entre
s y el camino recorrido entre 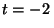 s y
s y 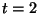 s.
s.
Problema 17:
Dos autos 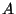 y
y 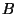 se mueven en la misma dirección con velocidad
se mueven en la misma dirección con velocidad
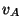 y
y 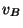 . Cuando el auto
. Cuando el auto 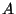 se encuentra una distancia
se encuentra una distancia 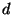 detrás de
detrás de 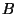 se aplican los frenos de
se aplican los frenos de 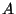 causando una
desaceleración constante
causando una
desaceleración constante 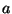 . Demostrar que para que no se
produzca un choque entre
. Demostrar que para que no se
produzca un choque entre 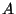 y
y 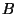 es necesario que:
es necesario que:
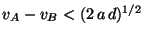
Problema 18:
El móvil 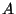 se mueve con una aceleración
se mueve con una aceleración
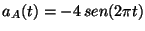 ;
se encuentra en
;
se encuentra en 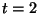 s en la posición
s en la posición 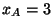 m siendo su
velocidad nula en
m siendo su
velocidad nula en
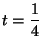 s. Calcule él
o los puntos de encuentro de
s. Calcule él
o los puntos de encuentro de 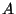 con un segundo móvil
con un segundo móvil 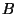 tal que
tal que
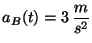 ,
, 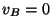 en
en 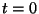 y
y
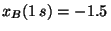 m.
m.
Problema 19:
Un tren viaja a una velocidad de
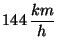 cuando de pronto el conductor advierte que en la misma vía,
cuando de pronto el conductor advierte que en la misma vía,
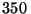 metros delante suyo se halla detenido otro tren.
Aplica inmediatamente los frenos que le producen una desaceleración
constante de
metros delante suyo se halla detenido otro tren.
Aplica inmediatamente los frenos que le producen una desaceleración
constante de
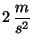 . Cuando lleva
recorridos
. Cuando lleva
recorridos 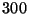 metros, el segundo tren al advertir que va a ser
embestido logra ponerse en movimiento con aceleración constante.
metros, el segundo tren al advertir que va a ser
embestido logra ponerse en movimiento con aceleración constante.
a) ¿Cuál es el valor mínimo de la
aceleración del segundo tren necesaria para evitar la colisión?
b) ¿Cuál es la velocidad de ambos trenes en el
momento de máxima proximidad? Realize los cálculos utilizando la
aceleración encontrada en a).
c) Suponiendo que el segundo tren arranca con una
aceleración de
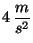 , cuánto vale la
mínima distancia a que llegarán a estar separados los trenes?
¿En que instante estarán a esa distancia?
, cuánto vale la
mínima distancia a que llegarán a estar separados los trenes?
¿En que instante estarán a esa distancia?
Problema 20:
Dos automóviles se acercan el uno hacia el otro a
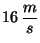 y
y
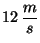 respectivamente. Cuando se encuentran separados por
respectivamente. Cuando se encuentran separados por 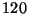 metros,
los dos conductores se dan cuenta de la situación y aplican los
frenos. Llegan al reposo al mismo tiempo, justo antes de chocar.
Suponiendo una desaceleración constante para los dos automóviles,
calcular:
metros,
los dos conductores se dan cuenta de la situación y aplican los
frenos. Llegan al reposo al mismo tiempo, justo antes de chocar.
Suponiendo una desaceleración constante para los dos automóviles,
calcular:
a) El tiempo necesario para que se detengan.
b) La aceleración de cada automóvil.
c) El camino recorrido por cada auto durante la
frenada.
Problema 21:
Un grifo deja caer gotas de agua a intervalos iguales de tiempo.
Cuando una determinada gota 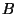 empieza su caída libre, la gota
precedente
empieza su caída libre, la gota
precedente 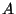 ha descendido ya
ha descendido ya 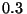 metros. Determinar la
distancia que habrá descendido la gota
metros. Determinar la
distancia que habrá descendido la gota 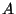 durante el tiempo en que
la distancia entre
durante el tiempo en que
la distancia entre 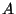 y
y 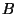 haya aumentado a
haya aumentado a 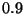 metros.
metros.
Problema 22:
La función de movimiento de un cuerpo respecto de un sistema 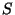 es
es
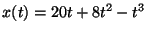 .
.
a) Transforme esta función de tal forma que dé
las coordenadas del cuerpo respecto de un sistema 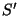 cuyo origen se
halla a
cuyo origen se
halla a 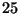 cm a la izquierda de
cm a la izquierda de 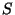 .
.
b) Escriba una nueva función de movimiento que dé
las coordenadas del cuerpo respecto a un tercer sistema 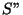 que se
mueve en la dirección x hacia la derecha con
que se
mueve en la dirección x hacia la derecha con
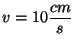 respecto a
respecto a 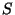 y cuyo origen en
y cuyo origen en
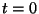 coincide con el origen de
coincide con el origen de 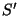 .
.
c) Calcule las expresiones generales de la
aceleración y la velocidad del cuerpo en función del tiempo
respecto a los tres sistemas.
d) Grafique y compare.
Problema 23:
Desde un montacargas que sube con una velocidad de
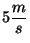 se deja caer una piedra que llega al suelo en
se deja caer una piedra que llega al suelo en 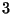 s.
a) ¿A qué altura estaba el montacargas cuando se
dejó caer la piedra?
b) ¿Con que velocidad chocó la piedra contra el
suelo?
s.
a) ¿A qué altura estaba el montacargas cuando se
dejó caer la piedra?
b) ¿Con que velocidad chocó la piedra contra el
suelo?
Problema 24:
Un ascensor de carga se mueve hacia arriba con velocidad constante de
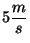 y pasa a un ascensor de pasajeros que
está quieto. Tres segundos más tarde parte hacia arriba el
ascensor de pasajeros con una aceleración de
y pasa a un ascensor de pasajeros que
está quieto. Tres segundos más tarde parte hacia arriba el
ascensor de pasajeros con una aceleración de
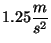 . Cuando el ascensor de pasajeros alcanza la velocidad
de
. Cuando el ascensor de pasajeros alcanza la velocidad
de
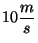 , continúa con velocidad
constante. Dibujar los diagramas
, continúa con velocidad
constante. Dibujar los diagramas 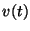 y
y 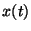 y hallar a partir de
ellos el tiempo y la distancia necesarios para que el ascensor de
pasajeros alcance al de carga.
y hallar a partir de
ellos el tiempo y la distancia necesarios para que el ascensor de
pasajeros alcance al de carga.
Problema 25:
Por el pozo de una mina caen gotas de agua a intervalos
constantes de 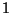 s. Un ascensor sube por el pozo a velocidad
constante de
s. Un ascensor sube por el pozo a velocidad
constante de
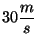 y es golpeado por una
gota de agua cuando se encuentra a
y es golpeado por una
gota de agua cuando se encuentra a 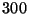 metros por debajo del
nivel de tierra. ¿Cuándo y dónde golpeará al ascensor la
siguiente gota?
metros por debajo del
nivel de tierra. ¿Cuándo y dónde golpeará al ascensor la
siguiente gota?
Fa.M.A.F ©1996
Pedro Pury
2001-02-07
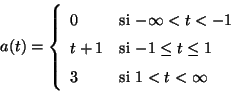
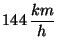 cuando de pronto el conductor advierte que en la misma vía,
cuando de pronto el conductor advierte que en la misma vía,