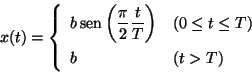Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Introducción a la Física
Guía N 6
Ejemplos de Problemas de Examen
6
Ejemplos de Problemas de Examen
Problema 1:
Considere una partícula cuya aceleración está dada por:
donde 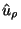 es el versor polar en la dirección radial en
el plano x-y, y
es el versor polar en la dirección radial en
el plano x-y, y 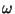 es una constante.
Suponga que en el instante inicial dicha partícula se encuentra
en la posición
es una constante.
Suponga que en el instante inicial dicha partícula se encuentra
en la posición
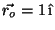 y su velocidad es
y su velocidad es
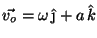 (donde la unidad
de distancia está en metros y la de tiempo en segundos).
(donde la unidad
de distancia está en metros y la de tiempo en segundos).
a) Escriba el vector posición 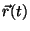 de la
partícula.
de la
partícula.
b) Calcule la aceleración tangencial y normal a la
trayectoria.
c) Interprete el significado físico de la
constante 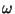 .
.
d) Dibuje la trayectoria.
Problema 2:
Un joven agita una botella de champagne parado sobre el borde de una
pista de baile circular de 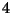 m de radio que gira con una velocidad
angular de
m de radio que gira con una velocidad
angular de 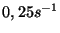 . Considere que en el momento de saltar el
corcho, la botella apuntaba radialmente hacia fuera de la pista,
formando el eje de la botella un ángulo de
. Considere que en el momento de saltar el
corcho, la botella apuntaba radialmente hacia fuera de la pista,
formando el eje de la botella un ángulo de 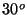 con la normal al
piso, y que se encontraba elevada a una altura de
con la normal al
piso, y que se encontraba elevada a una altura de 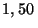 m respecto
del piso del salón de baile.
m respecto
del piso del salón de baile.
a) Si el corcho toca el piso del salón (sin haber
encontrado ningún otro obstáculo en su camino) habiendo
recorrido una distancia de 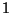 m medida sobre el piso del salón;
cuál es la velocidad inicial del corcho respecto de la botella?
m medida sobre el piso del salón;
cuál es la velocidad inicial del corcho respecto de la botella?
b) Describa el movimiento del corcho desde una mesa
en el salón lejos de la pista (Es decir escriba el vector
posición del corcho como función del tiempo).
c) ¿Cuál es la distancia angular recorrida por el
joven en la pista desde que salta el corcho hasta que toca el piso?
Problema 3:
Considere un cañon cuya longitud es 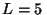 m, el cual forma un
ángulo
m, el cual forma un
ángulo 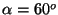 con la horizontal. La bala ubicada en el
fondo del cañon se encuentra a nivel del terreno. Al ser disparada,
la bala es acelerada dentro del cañon, desde su posición inicial
de reposo hasta que alcanza la boca de salida, según la función:
con la horizontal. La bala ubicada en el
fondo del cañon se encuentra a nivel del terreno. Al ser disparada,
la bala es acelerada dentro del cañon, desde su posición inicial
de reposo hasta que alcanza la boca de salida, según la función:
donde
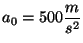 .
.
a) Determine el instante de tiempo 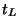 en el cual
la bala alcanza la boca del cañon, y la velocidad
en el cual
la bala alcanza la boca del cañon, y la velocidad 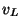 con la cual
es expulsada. Grafique la velocidad
con la cual
es expulsada. Grafique la velocidad 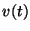 y la aceleración
y la aceleración 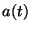 de la bala en su trayecto dentro del cañon.
de la bala en su trayecto dentro del cañon.
b) Calcule el instante de tiempo en el que la bala
disparada llega al nivel del terreno. Considere la aceleración de
la gravedad
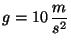 .
.
c) Calcule la distancia horizontal que recorre la
bala, desde su posición inicial de reposo.
d) Calcule el instante de tiempo en el cual la bala
alcanza la altura máxima.
e) ¿Es este tiempo la mitad del calculado en el
punto b)? Explique.
f) Calcule la distancia horizontal recorrida por la
bala cuando se encuentra a máxima altura.
g) Calcule las componentes tangencial y normal a la
trayectoria de la aceleración de la bala para todo 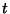 .
.
h) Cuando la bala se encuentra a máxima altura,
realice un diagrama vectorial de las componentes tangencial y normal
de la aceleración sobre el gráfico de la trayectoria.
Problema 4:
Un barco y un submarino viajan en el mar uno sobre el otro hacia el
Norte a
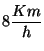 . El capitán del barco no
advierte que en un dado instante comienza a navegar sobre una
corriente superficial de
. El capitán del barco no
advierte que en un dado instante comienza a navegar sobre una
corriente superficial de
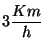 en la
dirección NE (
en la
dirección NE (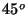 respecto al Norte). En el mismo instante el
capitán del submarino pone rumbo al Este con una velocidad de
respecto al Norte). En el mismo instante el
capitán del submarino pone rumbo al Este con una velocidad de
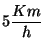 .
.
a) Calcule el desplazamiento del barco respecto del
submarino 15 minutos luego del instante de separación.
b) Si ahora el submarino deseara alcanzar al barco,
¿Hacia donde debe colocar su rumbo, suponiendo que su velocidad
respecto al agua es de
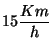 y que la
velocidad del barco y de la corriente superficial siguen siendo las
mismas?; ¿Cuanto tiempo le llevará al submarino alcanzar al barco.
y que la
velocidad del barco y de la corriente superficial siguen siendo las
mismas?; ¿Cuanto tiempo le llevará al submarino alcanzar al barco.
Problema 5:
La trayectoria de una partícula en el plano es:
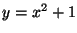 ;
y se tiene la siguiente función de movimiento:
;
y se tiene la siguiente función de movimiento:
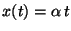 ,
donde la constante
,
donde la constante 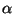 es una incógnita.
Un segundo móvil se desplaza en el mismo plano, libre de
aceleración, con una velocidad de módulo
es una incógnita.
Un segundo móvil se desplaza en el mismo plano, libre de
aceleración, con una velocidad de módulo 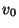 y en
y en 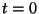 su
coordenada
su
coordenada 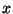 es nula.
Si en el instante
es nula.
Si en el instante 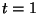 s ambos móviles se encuentran de manera
tal que se hallan en reposo relativo, determine para el segundo
móvil su vector posición como función del tiempo y
calcule el valor de la constante
s ambos móviles se encuentran de manera
tal que se hallan en reposo relativo, determine para el segundo
móvil su vector posición como función del tiempo y
calcule el valor de la constante 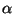 .
.
Problema 6:
Discuta la validez de la siguiente afirmación:
`` En los puntos de la trayectoria de una partícula en los
cuales su velocidad es nula, el vector aceleración es tangente a la
trayectoria''.
Problema 7:
En la matinee del último domingo, se vió un indio Sioux que
cabalgaba por un desfiladero de montaña sobre su caballo a
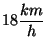 (esta velocidad sólo posee
componente horizontal). Perpendicular al desfiladero corría un
camino recto por el cual se desplazaba una carreta con un cargamento
de whisky. Cuando la carreta se hallaba en el cruce del camino con el
desfiladero, el indio, que en ese momento se encontraba a
(esta velocidad sólo posee
componente horizontal). Perpendicular al desfiladero corría un
camino recto por el cual se desplazaba una carreta con un cargamento
de whisky. Cuando la carreta se hallaba en el cruce del camino con el
desfiladero, el indio, que en ese momento se encontraba a 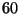 m de
dicho cruce (distancia horizontal) y a una altura de
m de
dicho cruce (distancia horizontal) y a una altura de 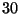 m sobre el
nivel del camino, disparó una flecha con una velocidad de
m sobre el
nivel del camino, disparó una flecha con una velocidad de
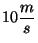 respecto al arco. Considerando que la
flecha es disparada formando un ángulo de
respecto al arco. Considerando que la
flecha es disparada formando un ángulo de 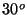 elevada con
respecto a la horizontal y que finalmente atraviesa al conductor de
la carreta. Calcule:
a) la dirección (en el plano horizontal) con la
cual la flecha fue lanzada,
b) la velocidad de la carreta,
c) el tiempo que tarda la flecha en alcanzar el
blanco desde que fue lanzada.
elevada con
respecto a la horizontal y que finalmente atraviesa al conductor de
la carreta. Calcule:
a) la dirección (en el plano horizontal) con la
cual la flecha fue lanzada,
b) la velocidad de la carreta,
c) el tiempo que tarda la flecha en alcanzar el
blanco desde que fue lanzada.
Problema 8:
Un aficionado al tango colocó en su viejo fonógrafo un disco de
Carlos Gardel. Cuando comenzó a sonar, el tanguero se percató que
la placa fonográfica de 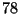 r.p.m. (revoluciones por minuto)
estaba girando a
r.p.m. (revoluciones por minuto)
estaba girando a 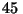 r.p.m.. Al cambiar el selector de velocidad
del fonógrafo, el disco pasó de manera uniforme de girar a
r.p.m.. Al cambiar el selector de velocidad
del fonógrafo, el disco pasó de manera uniforme de girar a
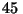 r.p.m. a girar a
r.p.m. a girar a 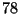 r.p.m. en
r.p.m. en 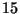 segundos; tras lo cual
permaneció con velocidad angular constante y la voz del zorzal
criollo se escuchó con inigualable nitidez.
Inadvertida por el tanguero, una hormiga negra se hallaba sujeta en
la periferia del disco e inmóvil respecto de este. Asumiendo que el
disco tiene un diámetro de
segundos; tras lo cual
permaneció con velocidad angular constante y la voz del zorzal
criollo se escuchó con inigualable nitidez.
Inadvertida por el tanguero, una hormiga negra se hallaba sujeta en
la periferia del disco e inmóvil respecto de este. Asumiendo que el
disco tiene un diámetro de 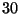 cm:
cm:
a) Calcule el vector aceleración de la
hormiga desde el instante en que se cambia el selector de velocidad
en adelante.
La hormiga harta de los tangos decide dejar el disco y comienza a
caminar hacia el centro de manera tal que, con respecto al disco,
describe un camino perfectamente radial.
b) Suponiendo la velocidad de la hormiga respecto del
disco constante: Exprese el vector aceleración de la hormiga
respecto al fonógrafo, como función de la distancia radial al
centro del disco.
Problema 9:
En una centrifugadora se coloca un tubo de ensayos con una muestra
líquida desconocida. Al conectarse la centrifugadora, esta
produce una aceleración angular dada por:
donde 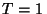 minuto y
minuto y 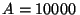 r.p.m.
r.p.m.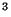 .
Al girar, el tubo de ensayos adopta una posición casi horizontal,
quedando la gota líquida a
.
Al girar, el tubo de ensayos adopta una posición casi horizontal,
quedando la gota líquida a 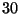 cm del centro de giro y a una
altura de
cm del centro de giro y a una
altura de 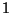 m del piso. Cuando la velocidad angular alcanza el
valor de
m del piso. Cuando la velocidad angular alcanza el
valor de 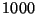 r.p.m., la muestra se solidifica repentinamente y se
rompe el tubo de ensayos liberando la misma.
r.p.m., la muestra se solidifica repentinamente y se
rompe el tubo de ensayos liberando la misma.
a) Calcule cuanto tiempo trascurrió desde que se
conecta la centrifugadora hasta que llega a 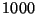 r.p.m..
r.p.m..
b) Si en el instante en que se libera la gota su
velocidad es perpendicular a una pared del laboratorio a 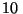 m del
centro de la centrifugadora, determine si la gota impacta contra la
pared y a qué altura del piso lo hace.
m del
centro de la centrifugadora, determine si la gota impacta contra la
pared y a qué altura del piso lo hace.
Problema 10:
Conocida la trayectoria de una partícula 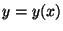 , puede
afirmarse inmediatamente que
, puede
afirmarse inmediatamente que
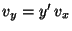 ; donde
; donde
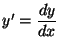 . Demuestre a continuación, que la
derivada respecto al tiempo del módulo de la velocidad
. Demuestre a continuación, que la
derivada respecto al tiempo del módulo de la velocidad 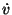 cumple:
cumple:
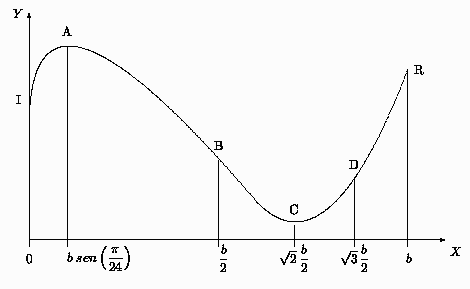
En la figura se muestra la trayectoria de un móvil sobre el plano
 . Se conoce además la siguiente función de movimiento:
. Se conoce además la siguiente función de movimiento:
a) Grafique para todo 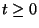 las siguientes
funciones:
las siguientes
funciones: 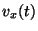 y
y 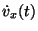 .
.
b) Determine en que instantes de tiempo el móvil se
encuentra en cada uno de los puntos destacados sobre la figura
(I, A, B, C, D, R).
c) Utilizando la información disponible, determine
si la aceleración tangencial es paralela o antiparalela al vector
velocidad en cada uno de los puntos destacados sobre la figura.
Explique en cada uno de los casos su razonamiento.
d) Sobre la figura dibuje un posible vector
aceleración para el móvil en cada uno de los puntos destacados.
e) Determine en qué regiones de la trayectoria el
movimiento puede ser acelerado; esto es, 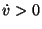 . Explique sus
conclusiones.
. Explique sus
conclusiones.
Fa.M.A.F ©1996
Pedro Pury
2001-02-07
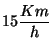 y que la
velocidad del barco y de la corriente superficial siguen siendo las
mismas?; ¿Cuanto tiempo le llevará al submarino alcanzar al barco.
y que la
velocidad del barco y de la corriente superficial siguen siendo las
mismas?; ¿Cuanto tiempo le llevará al submarino alcanzar al barco.
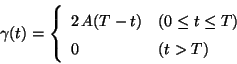
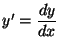 . Demuestre a continuación, que la
derivada respecto al tiempo del módulo de la velocidad
. Demuestre a continuación, que la
derivada respecto al tiempo del módulo de la velocidad