Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Introducción a la Física
Guía N 1
1
Problema 1: Calcule los valores de 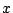 que satisfacen las siguientes
ecuaciones:
que satisfacen las siguientes
ecuaciones:
Nota: No utilice calculadora!! Para cada caso despeje 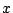 en
término de fracciones y radicales reducidos.
en
término de fracciones y radicales reducidos.
Problema 2: Ubique en un gráfico los puntos 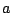 ,
, 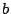 ,
, 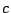 y
y 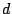 cuyas coordenadas son:
cuyas coordenadas son: 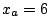 m;
m; 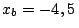 m;
m; 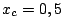 m
y
m
y 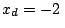 m.
Calcule la distancia que hay entre ellos, tomándolos de a pares.
m.
Calcule la distancia que hay entre ellos, tomándolos de a pares.
Problema 3: A un tramo recto de una ruta puede asociarse un sistema de
coordenadas, respecto al cual se refieren las coordenadas de los
objetos, personas, vehículos, etc. Dado un origen en el punto
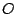 , las coordenadas de un semáforo
, las coordenadas de un semáforo 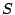 y un poste telefónico
y un poste telefónico
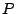 resultan
resultan 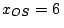 km y
km y
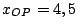 km. Indicar las
coordenadas del semáforo y del poste respecto de una estación
de servicio ubicada en
km. Indicar las
coordenadas del semáforo y del poste respecto de una estación
de servicio ubicada en 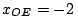 km respecto del sistema con
origen en
km respecto del sistema con
origen en 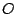 .
.
Problema 4: Los puntos  ,
, 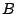 ,
, 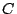 y
y 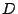 están consecutivamente
dispuestos sobre una recta desde la derecha hacia la izquierda.
Las distancias entre algunos pares de puntos son:
están consecutivamente
dispuestos sobre una recta desde la derecha hacia la izquierda.
Las distancias entre algunos pares de puntos son:
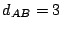 m,
m, 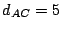 m,
m, 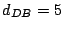 m.
Calcular las coordenadas de todos los puntos si elegimos,
respectivamente, el origen de coordenadas en los puntos:
a)
m.
Calcular las coordenadas de todos los puntos si elegimos,
respectivamente, el origen de coordenadas en los puntos:
a)  , b) B, c) C, d) D y
e)
, b) B, c) C, d) D y
e) 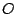 , siendo
, siendo 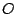 un punto elegido por Ud.
un punto elegido por Ud.
Problema 5: Considere nuevamente el Problema 2. Si ahora se considera
como origen de coordenadas al punto 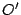 , situado entre los puntos
, situado entre los puntos
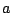 y
y 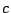 a
a 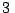 m de distancia del punto
m de distancia del punto 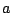 ,
expresar las coordenadas de todos lo puntos respecto de
,
expresar las coordenadas de todos lo puntos respecto de 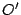 .
Calcular las distancias entre todos los posibles pares de puntos.
.
Calcular las distancias entre todos los posibles pares de puntos.
Problema 6: Sobre un camino unidimensional con origen en un punto  se
han indicado las coordenadas de Ernesto y de su tía, las cuales
son
se
han indicado las coordenadas de Ernesto y de su tía, las cuales
son 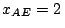 m y
m y 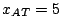 m respectivamente.
m respectivamente.
a) Calcular la distancia entre Ernesto y su tía.
b) Si ahora se considera como origen de las
coordenadas al punto 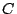 , tal que
, tal que 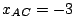 m, indique
las coordenadas de Ernesto y de su tía con respecto al nuevo
origen
m, indique
las coordenadas de Ernesto y de su tía con respecto al nuevo
origen 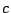 . ¿Cuál es ahora la distancia resultante entre
Ernesto y su tía, si ambos permanecen sentados durante todo
el problema. Discuta el resultado.
. ¿Cuál es ahora la distancia resultante entre
Ernesto y su tía, si ambos permanecen sentados durante todo
el problema. Discuta el resultado.
Problema 7: Considere un cuerpo que se mueve verticalmente partiendo de
un punto de coordenada 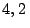 m y que pasa en forma sucesiva por los
puntos de coordenadas
m y que pasa en forma sucesiva por los
puntos de coordenadas 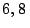 m,
m, 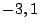 m,
m, 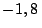 m y
m y  m,
para detenerse finalmente en el punto de coordenada
m,
para detenerse finalmente en el punto de coordenada 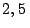 m.
Calcule:
m.
Calcule:
a) la longitud del camino recorrido en la zona de
coordenadas negativas,
b) la longitud total del camino recorrido y
c) la distancia entre los puntos de partida y
llegada.
Problema 8: Un automóvil que gasta 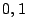 litros de nafta por
kilómetro, recorre un camino que une los puntos
litros de nafta por
kilómetro, recorre un camino que une los puntos 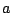 ,
, 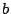 ,
, 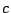 y
y 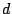 en ese orden. Si las coordenadas de esos puntos son:
en ese orden. Si las coordenadas de esos puntos son:
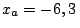 km;
km; 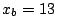 km;
km; 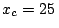 km y
km y 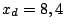 km,
calcule cuánta nafta gastó en su recorrido desde
km,
calcule cuánta nafta gastó en su recorrido desde 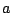 hasta
hasta 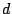 y a que distancia del punto de partida se encuentra el auto al
terminar su recorrido.
y a que distancia del punto de partida se encuentra el auto al
terminar su recorrido.
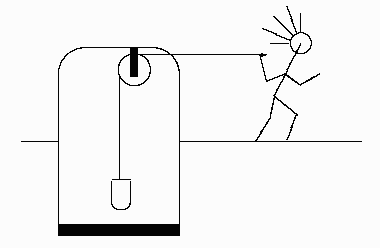
Problema 9: Un hombre saca agua de un pozo con un balde tirando de la
soga como se muestra en la figura. Cuando el balde se encuentra
sumergido al nivel de la superficie del agua, el hombre se halla
en un punto cuya coordenada es 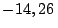 m respecto de algún origen
sobre su camino horizontal. Al llegar el balde al nivel del brocal,
el hombre se encuentra en el punto de ordenada
m respecto de algún origen
sobre su camino horizontal. Al llegar el balde al nivel del brocal,
el hombre se encuentra en el punto de ordenada 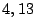 m respecto
del mismo origen. Calcular la longitud mínima que debe tener la
soga para poder sacar agua del pozo.
m respecto
del mismo origen. Calcular la longitud mínima que debe tener la
soga para poder sacar agua del pozo.
Problema 10: Un hombre no posee reloj pulsera, pero tiene un excelente
reloj de péndulo en su casa. Sin embargo este no se encuentra en
hora. Una tarde al salir de su casa observa su reloj y camina hasta
la casa de su amigo, a quien desea visitar. Al entrar y salir de la
casa de su amigo registra la hora oficial anunciada en el televisor.
Al llegar a su casa, vuelve a observar la hora de su antiguo reloj
y logra ajustarlo acorde a la hora oficial.
Explique como se puede colocar el reloj en hora con sólo los dos
pares de tiempos observados.
¿Qué suposiciones se asumen para realizar esta operación?
Problema 11: En cada uno de los siguientes casos, dar una expresión
matemática para la función descripta:
a) Un rectángulo tiene área  . Expresar el
perímetro
. Expresar el
perímetro 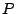 en función de la longitud de uno de sus lados y
la constante
en función de la longitud de uno de sus lados y
la constante  .
.
b) Un rectángulo está inscripto en una
semicircunferencia de radio 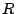 , con una de sus bases sobre el
diámetro. Expresar el área del rectángulo como función de la
longitud de su base y la constante
, con una de sus bases sobre el
diámetro. Expresar el área del rectángulo como función de la
longitud de su base y la constante 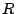 .
.
c) Para cercar dos parcelas de terreno, una circular
y la otra cuadrada, se han utilizado 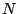 metros de cerco. Expresar
el área total cercada como función de la longitud del lado del
cuadrado y la constante
metros de cerco. Expresar
el área total cercada como función de la longitud del lado del
cuadrado y la constante 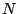 .
.
Problema 12: En coordenadas cartesianas ortogonales, determinar las
ecuaciones de las rectas que determinan los puntos 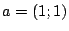 ,
,
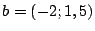 y
y 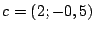 , tomados de a pares.
, tomados de a pares.
Problema 13: Si  ,
, 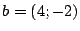 y
y 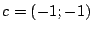 son tres de los
vértices de un paralelogramo
son tres de los
vértices de un paralelogramo 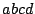 , hallar las coordenadas del
vértice
, hallar las coordenadas del
vértice 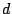 , las ecuaciones de las diagonales y graficar.
, las ecuaciones de las diagonales y graficar.
Problema 14: Representar gráficamente las siguientes funciones
y en cada caso determinar analítica y gráficamente los
puntos de intersección de la curva con los ejes 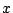 y
y 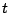 .
a)
.
a)
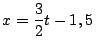 b)
b) 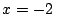 c)
c)
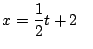 d)
d)
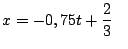 e)
e) 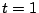 .
.
Problema 15: Dados los siguientes gráficos, encontrar una expresión
analítica para las correspondientes relaciones.
Problema 16: Representar gráficamente las siguientes funciones
y en cada caso determinar analítica y gráficamente
los puntos de intersección de la curva con los ejes 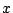 y
y 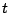 .
a)
.
a)
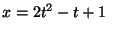 b)
b)
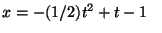 c)
c)
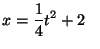 d)
d)
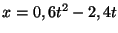
Problema 17: Determinar las constantes 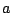 ,
, 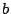 y
y 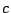 de función
cuadrática
de función
cuadrática
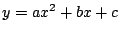 , de forma tal que su gráfica
pase por los puntos
, de forma tal que su gráfica
pase por los puntos 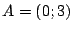 ,
, 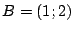 y
y 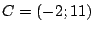 .
.
Problema 18: Dada la función
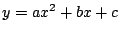 , graficar
cualitativamente cada uno de los siguientes casos:
, graficar
cualitativamente cada uno de los siguientes casos:
a) Suponga que 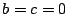 y considere las posibilidades:
i)
y considere las posibilidades:
i) 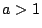 ; ii)
; ii) 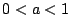 ; iii)
; iii)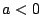 .
.
b) Suponga que 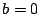 y considere las posibilidades:
i)
y considere las posibilidades:
i) 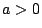 y
y 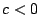 ; ii)
; ii) 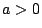 y
y 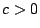 .
.
c) Suponga que 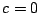 y considere las posibilidades:
i)
y considere las posibilidades:
i) 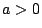 y
y 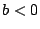 ; ii)
; ii) 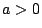 y
y 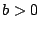 .
.
d) Suponga que 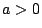 ,
, 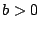 y
y 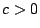 y estudie
los casos: i)
y estudie
los casos: i) 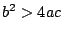 ; ii)
; ii) 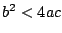 y iii)
y iii) 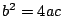 .
.
Problema 19: Calcular gráfica y analíticamente las intersecciones
entre la hipérbola
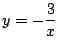 y la recta
y la recta
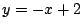 .
.
Problema 20: Representar gráficamente las siguientes funciones:
a)
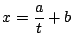 b)
b)
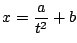 c)
c)
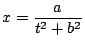
Problema 21: Representar gráficamente las siguientes funciones:
a) 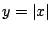 ,
b)
,
b) 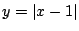 ,
c)
,
c) 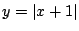 ,
e)
,
e)
Problema 22: Las funciones de movimiento de dos autos  y
y 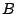 son
respectivamente:
son
respectivamente:
a) Determinar la distancia que separa a ambos
móviles en 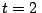 s.
b) ¿Para qué valor de
s.
b) ¿Para qué valor de 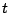 y en qué punto
y en qué punto 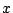 se
produce el encuentro de los autos? Resolver el problema analítica
y gráficamente.
se
produce el encuentro de los autos? Resolver el problema analítica
y gráficamente.
Problema 23: En el instante 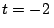 s parten un móvil
s parten un móvil  desde
desde
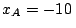 m y otro
m y otro 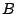 desde
desde 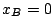 m. En
m. En 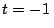 s,
s,
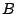 se halla en
se halla en 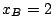 m, siendo en
m, siendo en 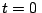 s la distancia
entre los móviles de
s la distancia
entre los móviles de 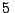 m.
m.
a) Determinar las funciones de movimiento de los
móviles  y
y 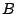 suponiendo que son de la forma
suponiendo que son de la forma 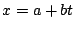 .
.
b) ¿Tiene el problema solución única?
¿Porqué?
c) Determine él o los puntos de encuentro en forma
gráfica y analítica.
Fa.M.A.F ©2003
Pedro Pury
2004-03-19
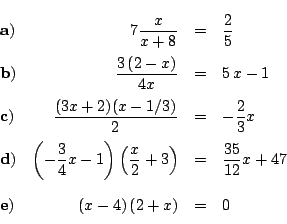
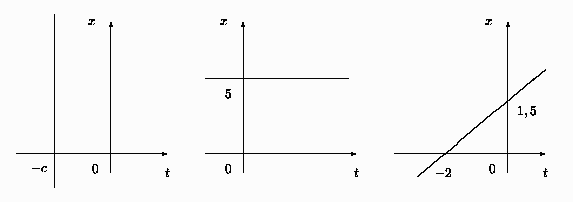
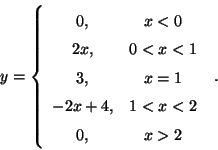
![\begin{displaymath}
\begin{array}{lcl}
x_A [m] &=& (1/2) [m/s] t [s] + 2,5 [m] \\
x_B [m] &=& -2 [m/s] t [s] + 4 [m]
\end{array}
\end{displaymath}](img91.png)