Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Introducción a la Física
Guía N 2
2
Problema 1:
a) Expresar en radianes los siguientes ángulos
dados en grados sexagesimales:
b) Expresar en grados, minutos y segundos
sexagesimales:
Problema 2:
Utilizando la circunferencia trigonométrica graficar las siguientes
funciones: tangente, cotangente, secante y cosecante en el intervalo
![$\left[0,2\pi \right]$](img8.png) .
.
Problema 3:
Conociendo que
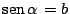 y que
y que 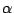 se encuentra
en el segundo cuadrante, calcule el valor de las restantes funciones
trigonométricas de
se encuentra
en el segundo cuadrante, calcule el valor de las restantes funciones
trigonométricas de 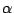 en términos de b.
en términos de b.
Problema 4:
Demostrar que:
a)
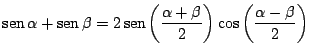 b)
b)
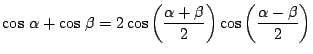
Problema 5:
Demostrar que:
Discrimine según el cuadrantre al cual pertenece
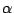 , cuál signo de la raiz cuadrada se aplica en a) y b).
, cuál signo de la raiz cuadrada se aplica en a) y b).
Problema 6:
Resolver gráficamente la ecuación:
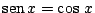 .
Encuentre una expresión general para los valores de
.
Encuentre una expresión general para los valores de 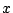 que son
soluciones de la ecuación anterior.
que son
soluciones de la ecuación anterior.
Problema 7:
Encuentre los valores de 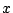 para los cuales:
para los cuales:
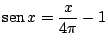 .
.
Problema 8:
Resolver la siguiente ecuación trascendente:
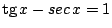 .
.
Problema 9:
Una torre proyecta una sombra de 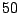 m cuando el sol está a
m cuando el sol está a
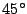 sobre el horizonte. Calcular la altura de la torre.
sobre el horizonte. Calcular la altura de la torre.
Problema 10:
A 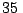 m del eje del obelisco de la ciudad de Buenos Aires se
sitúa un operador con un teodolito, quien encuentra que el
ángulo sustendido por el obelisco es de
m del eje del obelisco de la ciudad de Buenos Aires se
sitúa un operador con un teodolito, quien encuentra que el
ángulo sustendido por el obelisco es de
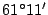 .
Calcule la altura del obelisco teniendo en cuenta que el instrumento
está a
.
Calcule la altura del obelisco teniendo en cuenta que el instrumento
está a 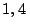 m del suelo.
m del suelo.
Problema 11:
Desde el espejo de un faro marino situado a 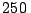 m sobre el nivel
del mar se observa un bote bajo un ángulo de depresión de
m sobre el nivel
del mar se observa un bote bajo un ángulo de depresión de
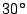 . Calcule la distancia horizontal entre el bote y el
faro.
. Calcule la distancia horizontal entre el bote y el
faro.
Problema 12:
Dos observadores en tierra, separados por una distancia de 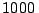 m,
observan un globo aerostático que se encuentra elevado entre ellos.
Ambos observadores y el globo se hallan en un mismo plano vertical.
Uno de los observadores mide un ángulo de elevación de
m,
observan un globo aerostático que se encuentra elevado entre ellos.
Ambos observadores y el globo se hallan en un mismo plano vertical.
Uno de los observadores mide un ángulo de elevación de
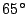 y el otro mide
y el otro mide 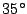 . Calcule la altura a la que
se encuentra el globo.
. Calcule la altura a la que
se encuentra el globo.
Problema 13:
Considere los polígonos regulares de n lados inscriptos en un
circunferencia de radio R.
a) Verifique que el perímetro de dichos
polígonos puede expresarse como:
b) Verifique que el área encerrada por dichos
polígonos puede expresarse como:
c) Grafique las funciones 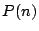 y
y 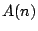 para
n = 3, 4, 5, 6 y 12 (considere
para
n = 3, 4, 5, 6 y 12 (considere 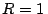 cm).
cm).
d) Teniendo en cuenta el límite notable
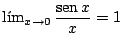 ,
encuentre los límites de las sucesiones
,
encuentre los límites de las sucesiones 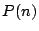 y
y 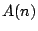 .
Interprete geométricamente estos resultados.
.
Interprete geométricamente estos resultados.
e) Encuentre el límite de la sucesión
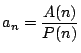 y compare con el
correspondiente cociente entre el área y el perímetro
del círculo.
y compare con el
correspondiente cociente entre el área y el perímetro
del círculo.
Problema 14:
Derivar aplicando la definición las siguientes funciones:
Problema 15:
Derive las siguientes funciones:
Problema 16:
Encontrar los puntos críticos de las siguientes funciones y
determinar si son máximos, mínimos o puntos de inflexión.
Graficar.
Problema 17:
Determinar la función cuadrática
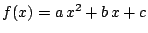 ,
tal que se anula para
,
tal que se anula para 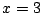 y
y 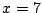 y tiene un mínimo en
y tiene un mínimo en
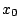 tal que
tal que 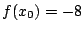 .
.
Problema 18:
Estudie la función:
para 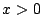 .
Considerando distintas posibilidades para el valor del
parámetro
.
Considerando distintas posibilidades para el valor del
parámetro 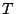 . En particular:
Grafique la función en cada uno de estos casos.
. En particular:
Grafique la función en cada uno de estos casos.
Problema 19:
¿Cuál es el área máxima que puede encerrar un rectángulo de
perímetro 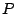 ?
?
Problema 20:
Determinar el rectángulo inscripto en la elipse de semiejes 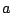 y
y
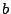 de lados paralelos a los ejes y de área máxima.
de lados paralelos a los ejes y de área máxima.
Problema 21:
Se quiere construir una caja sin tapa con una hoja de cartón de
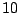 cm x
cm x 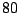 cm. ¿Cuáles serán las dimensiones de la caja
para que tenga capacidad máxima?.
cm. ¿Cuáles serán las dimensiones de la caja
para que tenga capacidad máxima?.
Problema 22:
Sea la función
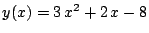 . Calcular la diferencia
entre
. Calcular la diferencia
entre 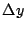 y
y 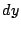 en
en 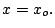
Problema 23:
¿Cuál debe ser la longitud de un hilo que rodee la Tierra por una
circunferencia máxima?. Si repetimos la operación de manera tal
que exista 1 cm entre el hilo y la Tierra, cuánto debemos
aumentar la longitud del hilo?. Utilice diferenciales para el
cálculo y compare con el valor exacto de variación de la
longitud.
Problema 24:
Suponga que se quiere rodear la Tierra con una esfera metálica de
forma tal que exista entre ambas una capa de aire de 1 cm de espesor.
¿Cuánto más grande debe ser la superficie de la esfera respecto
de la superficie de la Tierra?. ¿Y su volumen?. Utilice
diferenciales para el cálculo y compare con los valores exactos de
la variación de la superficie y el volumen.
(Radio de la Tierra: 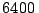 Km).
Km).
Problema 25:
La medida del diámetro de un círculo es 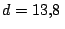 cm, con
un error por defecto menor que
cm, con
un error por defecto menor que 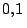 cm. Calcular mediante la
diferencial el error cometido en la determinación de la superficie.
cm. Calcular mediante la
diferencial el error cometido en la determinación de la superficie.
Comparar con el valor exacto de 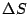 .
.
Problema 26:
Demostrar que el error relativo cometido en la determinación del
área 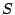 de un círculo es igual al doble del error relativo del
radio
de un círculo es igual al doble del error relativo del
radio 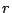 (se define como error relativo de una magnitud
(se define como error relativo de una magnitud 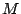 al
cociente
al
cociente 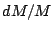 ).
Compare
).
Compare 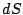 con el valor exacto de
con el valor exacto de 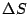 para
para
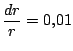 y
y 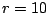 .
.
Problema 27:
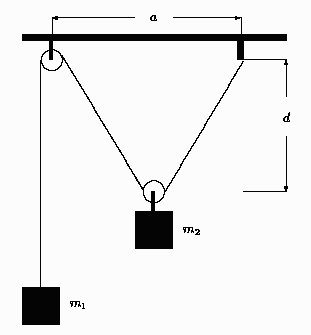
La figura muestra un sistema compuesto por las masas 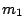 y
y 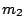 las cuales se hallan suspendidas de forma tal que mientras
las cuales se hallan suspendidas de forma tal que mientras
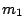 está atada a un extremo de la cuerda,
está atada a un extremo de la cuerda, 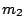 está colgada
del eje de la polea la cual puede deslizar libremente sobre la
cuerda. La longitud total de la cuerda es
está colgada
del eje de la polea la cual puede deslizar libremente sobre la
cuerda. La longitud total de la cuerda es 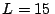 m,
m, 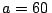 cm
y
cm
y 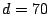 cm. Los radios de ambas poleas son despreciables frente a
las dimensiones de
cm. Los radios de ambas poleas son despreciables frente a
las dimensiones de 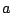 y
y 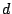 .
.
a) Si la masa 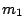 se desplaza
se desplaza 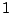 cm hacia abajo, hallar
el desplazamiento de la masa
cm hacia abajo, hallar
el desplazamiento de la masa 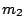 utilizando la diferencial. No
utilice calculadora. Compare con el desplazamiento exacto ocurrido.
utilizando la diferencial. No
utilice calculadora. Compare con el desplazamiento exacto ocurrido.
b) Suponiendo que 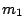 se desplaza con velocidad
se desplaza con velocidad 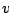 ,
calcule la velocidad de la masa
,
calcule la velocidad de la masa 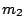 .
.
Problema 28:
Considere la siguiente función de movimiento de un cuerpo:
donde ![$[ x ] =\,$](img84.png) m y
m y ![$[ t ] =\,$](img85.png) s.
s.
a) Graficar la función 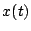 .
.
b) Determinar analíticamente en todos los casos y
gráficamente en los siete primeros, los valores de  (velocidad media del móvil) en los
siguientes intervalos de tiempo expresados en segundos:
(velocidad media del móvil) en los
siguientes intervalos de tiempo expresados en segundos:
![$[ -1,5 ]$](img88.png) ,
, ![$[ -1,4 ]$](img89.png) ,
, ![$[ -1,2 ]$](img90.png) ,
, ![$[ -1,1 ]$](img91.png) ,
,
![$[ -1,-0.5 ]$](img92.png) ,
, ![$[ -1,-0.8 ]$](img93.png) ,
, ![$[ -1,-0.9 ]$](img94.png) ,
, ![$[ -1,-0.99 ]$](img95.png) ,
,
![$[ -1,-0.999 ]$](img96.png) y
y
![$[ -1,-0.9999 ]$](img97.png) .
.
c) Sea
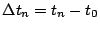 , con
, con 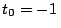 s y
s y
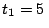 s,
s, 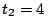 s,
s, 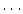 ,
,
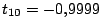 s. A
medida que
s. A
medida que 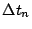 se hace más pequeño, a qué valor se
aproxima la velocidad media del móvil en el intervalo
se hace más pequeño, a qué valor se
aproxima la velocidad media del móvil en el intervalo
![$[ -1,-1 + \Delta t_n ]\,$](img105.png) s?. ¿Cómo se interpreta
geométricamente este resultado?.
s?. ¿Cómo se interpreta
geométricamente este resultado?.
d) Encuentre la ecuación de la recta tangente a la
función 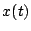 en
en 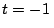 s.
s.
Problema 29:
Las coordenadas de dos móviles están dadas en función del
tiempo por:
Hallar la mínima distancia que separa a los móviles y
el instante en el que están en esa situación.
Graficar:
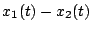 y
y
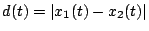
Problema 30:
Sabiendo que las funciones de movimiento de los móviles 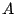 y
y 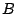 son respectivamente:
son respectivamente:
a) Calcule la distancia mínima que los separa y
el instante de tiempo 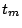 en que esto se produce.
en que esto se produce.
b) Calcule 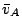 y
y 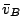 entre
entre 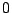 y
y
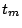 .
.
c) Calcule 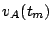 y
y 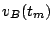 .
.
Fa.M.A.F ©2003
Pedro Pury
2004-03-19
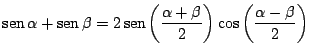
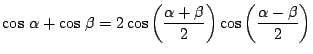
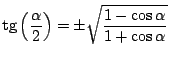 c)
c)
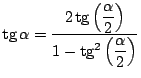
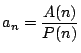 y compare con el
correspondiente cociente entre el área y el perímetro
del círculo.
y compare con el
correspondiente cociente entre el área y el perímetro
del círculo.
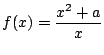
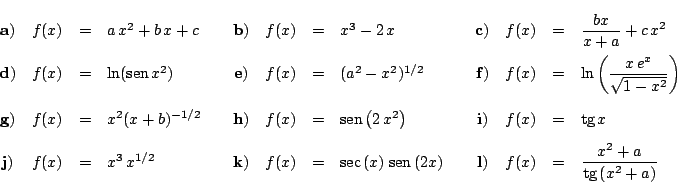
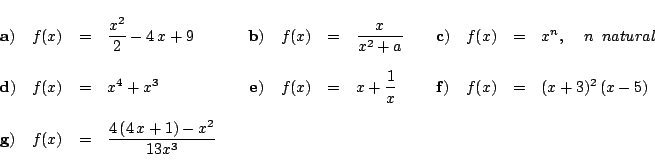
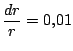 y
y