Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Introducción a la Física
Guía N 4
4
Problema 1:
¿Cuales son las componentes del vector que resulta de la diferencia
del vector
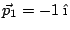 y el vector
y el vector
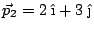 ?
Calcular el módulo del vector diferencia.
?
Calcular el módulo del vector diferencia.
Problema 2:
El vector 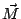 tiene módulo
tiene módulo 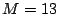 y su primera componente
es
y su primera componente
es 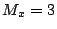 . ¿Cuál es el valor de la otra componente?
. ¿Cuál es el valor de la otra componente?
Problema 3:
Dados los vectores
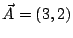 ;
;
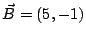 ;
;
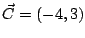 y
y
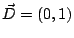 ,
determinar gráfica y analíticamente, las componentes, módulo,
dirección y sentido de los vectores:
,
determinar gráfica y analíticamente, las componentes, módulo,
dirección y sentido de los vectores:
Problema 4:
Sea el vector de componentes 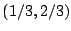 . Hallar las componentes del
vector de módulo
. Hallar las componentes del
vector de módulo 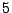 que tiene la misma dirección y sentido que
el vector dado.
que tiene la misma dirección y sentido que
el vector dado.
Problema 5:
Sean los vectores 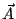 y
y 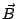 de módulo
de módulo 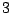 y
y 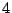 respectivamente.
respectivamente.
a) Calcule el módulo de la resultante de ambos
vectores cuando el ángulo comprendido entre ellos es
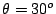 .
.
b) Haga lo mismo para
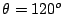 .
.
c) Calcule en ambos casos la dirección de la
resultante respecto del vector 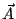 .
.
Problema 6:
Dados
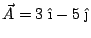 ;
;
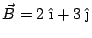 y
y
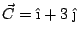 calcular:
calcular:
a)
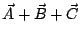
b)
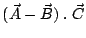
c) La distancia que hay entre los extremos de los
vectores 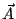 y
y 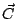 (ubicados ambos a partir del mismo
origen).
(ubicados ambos a partir del mismo
origen).
d) El ángulo que forman
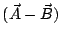 con
con
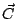 y
y
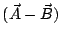 con
con 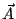 .
.
e) Encontrar un vector de módulo uno que sea
perpendicular a 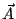 . ¿Cuántas soluciones pueden darse?
. ¿Cuántas soluciones pueden darse?
Problema 7:
Un avión vuela 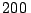 km hacia el NE en una dirección que
forma un ángulo de
km hacia el NE en una dirección que
forma un ángulo de 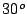 hacia el este de la dirección norte.
En ese punto cambia su dirección de vuelo hacia el NO. En esta
dirección vuela
hacia el este de la dirección norte.
En ese punto cambia su dirección de vuelo hacia el NO. En esta
dirección vuela 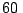 Km formando un ángulo de
Km formando un ángulo de 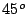 con la
dirección norte.
con la
dirección norte.
a) Calcular la máxima distancia hacia el este del
punto de partida a la que llegó el avión .
b) Calcular la máxima distancia hacia el norte del
punto de partida, a la que llegó el avión.
c) Calcular la distancia a la que se encuentra el
avión del punto de partida, al cabo de su recorrido.
Problema 8:
El movimiento de un cuerpo está dado paramétricamente por:
donde 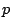 ,
, 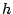 y
y 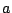 son constantes positivas.
son constantes positivas.
a) Escribir la ecuación de la trayectoria del cuerpo
y graficar.
b) Calcular la velocidad 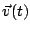 y la
aceleración
y la
aceleración 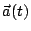 .
.
c) Determinar el instante de tiempo en que el cuerpo
se detiene y calcular 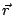 y
y 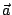 para ese instante.
para ese instante.
Problema 9:
El movimiento en el plano de una partícula está determinado
por:
donde
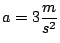 y
y
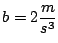 .
.
a) Calcular la trayectoria de la partícula.
Graficar.
b) Calcular la aceleración en
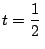 s.
s.
c) ¿Cuál es el ángulo que forman los vectores
velocidad y aceleración en ese instante?
d) Determinar el instante 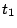 en que la
aceleración es paralela a la recta
en que la
aceleración es paralela a la recta 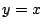 , y el instante
, y el instante 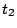 en que la velocidad es paralela a esa recta.
en que la velocidad es paralela a esa recta.
e) Determinar la velocidad media en el intervalo
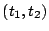 .
.
Problema 10:
Exprese las siguientes ecuaciones en coordenadas cartesianas y
grafique:
a)
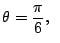 b)
b)
 c)
c)
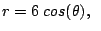 d)
d)
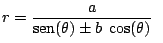 y
e)
y
e)
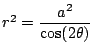 .
.
Problema 11:
Expresar la siguiente ecuación en coordenadas cartesianas:
y grafique considerando los siguientes casos:
a) 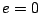
b) 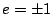
c) 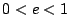 (graficar usando la exprexión dada en
polares).
(graficar usando la exprexión dada en
polares).
d) 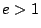 (intentar graficar la expresión en
cartesianas).
(intentar graficar la expresión en
cartesianas).
e) ¿Qué pasa si se cambia 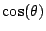 por
por
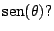
Problema 12:
Dos embarcaderos A y B, situados sobre un río, distan uno del
otro 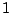 Km. Dos hombres han de realizar recorridos desde A hacia B
y volver. Uno de los hombres va remando en una barca a la velocidad
de
Km. Dos hombres han de realizar recorridos desde A hacia B
y volver. Uno de los hombres va remando en una barca a la velocidad
de
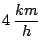 tespecto al río.
El otro realiza el trayecto por tierra a una velocidad de
tespecto al río.
El otro realiza el trayecto por tierra a una velocidad de
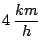 . La velocidad del río respecto
de tierra es de
. La velocidad del río respecto
de tierra es de
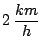 en la dirección de
A a B. ¿Cuánto tardará cada hombre en efectuar el recorrido?.
en la dirección de
A a B. ¿Cuánto tardará cada hombre en efectuar el recorrido?.
Problema 13:
Un piloto de avión desea volar hacia el norte. El viento sopla
hacia el oeste a
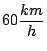 . Si la velocidad de
vuelo del avión es de
. Si la velocidad de
vuelo del avión es de
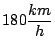 (velocidad
con aire en calma). ¿En qué dirección debe poner rumbo el
piloto?. ¿Cuál es la velocidad del avión respecto de tierra?.
Haga un diagrama vectorial.
(velocidad
con aire en calma). ¿En qué dirección debe poner rumbo el
piloto?. ¿Cuál es la velocidad del avión respecto de tierra?.
Haga un diagrama vectorial.
Problema 14:
Un piloto de avión pone su brújula hacia el oeste y mantiene su
velocidad respecto del aire en
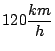 .
Después de volar media hora se encuentra sobre una ciudad situada
.
Después de volar media hora se encuentra sobre una ciudad situada
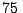 km hacia el oeste y
km hacia el oeste y 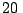 km al sur de su punto de partida.
km al sur de su punto de partida.
a) Calcular la velocidad del viento en magnitud y
dirección.
b) Si la velocidad del viento varía, siendo
ahora en dirección sur de
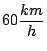 ,
¿En que dirección debería el piloto poner su rumbo a fin de
dirigirse hacia el oeste? (Tómese la velocidad del avión de
,
¿En que dirección debería el piloto poner su rumbo a fin de
dirigirse hacia el oeste? (Tómese la velocidad del avión de
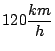 respecto del aire.)
respecto del aire.)
Problema 15:
Una gota de lluvia que cae verticalmente pega contra la ventana de un
tren que se mueve a razón de
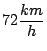 . La
gota marca una raya sobre el cristal que forma un ángulo de
. La
gota marca una raya sobre el cristal que forma un ángulo de 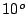 con la horizontal. ¿Cuál es la velocidad de caída de la gota?
con la horizontal. ¿Cuál es la velocidad de caída de la gota?
Problema 16:
Un río muy ancho tiene una corriente de
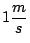 en la dirección positiva del eje
en la dirección positiva del eje 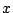 . Una lancha cuya
velocidad respecto al agua es de
. Una lancha cuya
velocidad respecto al agua es de
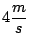 viaja
oblicuamente formando un ángulo de
viaja
oblicuamente formando un ángulo de 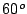 con la dirección
con la dirección
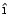 . En un momento dado, se deja caer desde la lancha
una botella que flota, y luego de
. En un momento dado, se deja caer desde la lancha
una botella que flota, y luego de 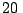 minutos se decide volver a
buscarla. Para lo cual la lancha se detiene y regresa manteniendo su
velocidad de
minutos se decide volver a
buscarla. Para lo cual la lancha se detiene y regresa manteniendo su
velocidad de
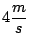 respecto al agua.
respecto al agua.
a) ¿Hacia dónde debe apuntar la lancha con respecto
a la dirección de la corriente para encontrar la botella?
b) ¿Cuánto tardará en regresar a la botella?
c) Describa el problema desde un sistema fijo en
tierra.
Fa.M.A.F ©2003
Pedro Pury
2004-03-19
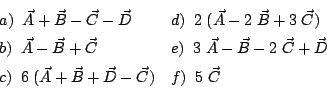
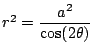 .
.
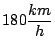 (velocidad
con aire en calma). ¿En qué dirección debe poner rumbo el
piloto?. ¿Cuál es la velocidad del avión respecto de tierra?.
Haga un diagrama vectorial.
(velocidad
con aire en calma). ¿En qué dirección debe poner rumbo el
piloto?. ¿Cuál es la velocidad del avión respecto de tierra?.
Haga un diagrama vectorial.
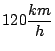 .
Después de volar media hora se encuentra sobre una ciudad situada
.
Después de volar media hora se encuentra sobre una ciudad situada
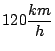 respecto del aire.)
respecto del aire.)