Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Introducción a la Física
Guía N 5
5
Problema 1:
Una bala es disparada horizontalmente por un cañon situado en una
plataforma de 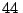 m de altura, con una velocidad de salida de
m de altura, con una velocidad de salida de
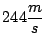 . Suponga el terreno horizontal y
perfectamente plano.
. Suponga el terreno horizontal y
perfectamente plano.
a) ¿Cuánto tiempo permanece la bala en el aire
antes de llegar al piso?
b) ¿Cuál es su alcance? Es decir, a qué
distancia del cañon choca con el piso?
c) ¿Cuál es la magnitud de la componente vertical
de la velocidad cuando llega al suelo?
d) Repita la parte c) para el caso en que la bala se
deja caer libremente desde la plataforma.
Problema 2:
Un jugador lanza una pelota, en una dirección que forma un
ángulo de 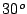 con la horizontal, con una velocidad inicial de
con la horizontal, con una velocidad inicial de
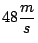 . Un segundo jugador, que se encuentra
a una distancia de
. Un segundo jugador, que se encuentra
a una distancia de 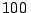 m en la dirección del lanzamiento, inicia
su carrera en el momento del lanzamiento en la dirección que va la
pelota; con el fin de tomarla.
m en la dirección del lanzamiento, inicia
su carrera en el momento del lanzamiento en la dirección que va la
pelota; con el fin de tomarla.
a) ¿Con qué velocidad debe correr el segundo
jugador para tomar la pelota justo antes de que esta llegue al suelo?
(Suponga que la velocidad de carrera es constante).
b) Calcule el ángulo de lanzamiento necesario para
lograr el máximo alcance con la misma velocidad inicial de la
pelota; y la velocidad del segundo jugador en este caso.
Problema 3:
Con un tubo de rayos catódicos se dispara horizontalmente un haz de
electrones con una velocidad de
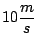 en la
región situada entre un par de placas horizontales de
en la
región situada entre un par de placas horizontales de 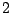 cm de
largo. Un campo eléctrico entre las placas ejerce sobre los
electrones una aceleración constante perpendicular a la dirección
inicial del haz, de
cm de
largo. Un campo eléctrico entre las placas ejerce sobre los
electrones una aceleración constante perpendicular a la dirección
inicial del haz, de
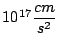 .
Encontrar:
.
Encontrar:
a) El desplazamiento del haz (dirección y magnitud)
cuando sale de las placas.
b) Si se coloca una pantalla a un metro de las placas
horizontales, ¿Cuál es el corrimiento del haz con respecto al
punto en que incidiría si no estuviese sujeto a dicha
aceleración?.
Problema 4:
Se disparan diversos proyectiles a una distancia horizontal R del
borde de un acantilado de altura h, de tal manera que lleguen al
suelo a una distancia horizontal 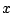 del pie del acantilado. Si Ud.
quiere que
del pie del acantilado. Si Ud.
quiere que 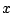 sea lo más chico posible, ¿Cómo ajustaría los
valores de
sea lo más chico posible, ¿Cómo ajustaría los
valores de 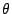 (ángulo de disparo respecto a la horizontal) y
(ángulo de disparo respecto a la horizontal) y
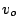 (velocidad inicial)?. Suponga que
(velocidad inicial)?. Suponga que 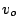 se puede incrementar
hasta cierto valor máximo y que
se puede incrementar
hasta cierto valor máximo y que 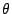 puede variar
continuamente.
puede variar
continuamente.
Problema 5:
Se apunta un rifle a un blanco colocado a una distancia 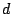 de la
boca del arma. Ambos están a una altura
de la
boca del arma. Ambos están a una altura 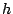 respecto del suelo
horizontal. Se deja caer el blanco libremente, mediante un mecanismo
que lo suelta en el momento en que la bala sale de la boca del rifle.
respecto del suelo
horizontal. Se deja caer el blanco libremente, mediante un mecanismo
que lo suelta en el momento en que la bala sale de la boca del rifle.
a) Determine el rango de velocidades inicial de la
bala de modo que dé en el blanco antes que este llegue al suelo.
b) ¿A qué altura del suelo choca contra el blanco
cuando se dispara con una velocidad inicial dentro de ese rango?
c) Si en lugar de lanzar horizontalmente la bala, se
dispara hacia arriba con un cierto ángulo y con una velocidad
inicial dentro del rango calculado en a) ¿Choca con el blanco
en algún momento? ¿Por qué? ¿Y si el disparo es con un
ángulo hacia abajo?
Problema 6:
El angulo 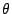 (en radianes) girado por una rueda, en función
del tiempo (en segundos) viene dado por
(en radianes) girado por una rueda, en función
del tiempo (en segundos) viene dado por
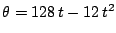 .
.
a) Calcule la velocidad y aceleración angulares al
cabo de 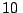 s.
s.
b) Grafique 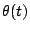 ,
, 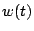 ,
, 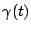 .
.
Problema 7:
La posición angular de una partícula que se mueve a lo largo de
una circunferencia de radio 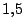 m está dada por la expresión:
m está dada por la expresión:
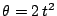 ; donde
; donde 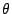 se da en radianes y t en
segundos.
se da en radianes y t en
segundos.
a) Calcule la aceleración tangencial, centrí
peta y total de la partícula para todo t.
b) Idem que a) para 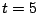 s y dibújelos sobre la
trayectoria.
s y dibújelos sobre la
trayectoria.
c) Calcule la aceleración angular 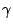 .
.
d) Grafique 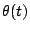 ,
, 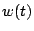 ,
, 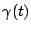 ,
,
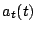 , y
, y 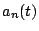 .
.
Problema 8:
Un cuerpo se mueve en el plano 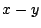 de manera que:
de manera que:
En estas expresiones 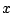 e
e 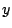 son las coordenadas del cuerpo,
son las coordenadas del cuerpo, 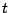 es
el tiempo, y
es
el tiempo, y 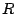 y
y 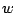 son constantes.
son constantes.
a) Encuentre la ecuación de la curva sobre la cual
se mueve el cuerpo. ¿Qué significa físicamente la constante
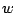 ?
?
b) Calcule las componentes 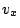 y
y 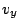 de la
velocidad, y la magnitud y dirección del vector
de la
velocidad, y la magnitud y dirección del vector 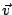 . Describa
el movimiento del cuerpo.
. Describa
el movimiento del cuerpo.
c) Calcule 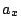 y
y 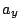 y además la magnitud y
dirección de la aceleración resultante.
y además la magnitud y
dirección de la aceleración resultante.
Problema 9:
Suponga un cuerpo que realiza un movimiento descripto por las
funciones:
siendo [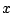 ] = metros, [
] = metros, [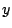 ] = metros, [
] = metros, [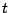 ] = segundos.
] = segundos.
a) Escribir los vectores  ,
, 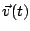 y
y
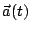 .
.
b) Calcular la aceleración tangencial y normal:
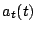 y
y 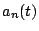 .
.
c) Calcular el valor de 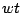 para el cual los
vectores
para el cual los
vectores  y
y 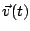 son perpendiculares. ¿Existen
otros valores de
son perpendiculares. ¿Existen
otros valores de 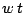 para los cuales se cumple esta condición?
para los cuales se cumple esta condición?
d) Determine la trayectoria del cuerpo.
Problema 10:
Una rueda gira con aceleracion angular 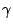 dada por:
dada por:
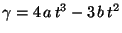 ; donde
; donde 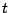 es el tiempo,
y
es el tiempo,
y 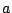 y
y 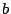 constantes. Si la rueda tiene velocidad inicial
constantes. Si la rueda tiene velocidad inicial 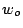 escriba las ecuaciones de:
escriba las ecuaciones de:
a) La velocidad angular y el ángulo descripto en
función del tiempo.
b) Grafique 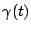 ,
, 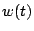 ,
, 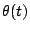 para
para
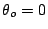 y
y 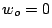 .
.
Problema 11:
La corona de una bicicleta cuyo radio es 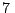 cm, parte del reposo y
aumenta su velocidad angular uniformemente a razon de
cm, parte del reposo y
aumenta su velocidad angular uniformemente a razon de
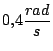 , por cada segundo. Dicha corona
transmite su movimiento a un piñon de
, por cada segundo. Dicha corona
transmite su movimiento a un piñon de 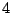 cm de radio.
cm de radio.
a) Obtener la relación entre las aceleraciones
angulares y los radios de la corona y el piñon.
b) Encontrar el tiempo necesario para que el piñon
alcance una frecuencia angular de 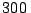 rpm.
rpm.
Problema 12:
El radio de la órbita terrestre (supuesta circular) es de
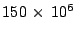 Km y la tierra la recorre en
Km y la tierra la recorre en 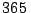 dias.
dias.
a) ¿Cuál es el módulo de la velocidad de la tierra
sobre su órbita en Km/h?
b) ¿Cuál es el módulo de la aceleración de la
tierra hacia el sol?
c) Escriba los vectores velocidad y aceleración de
la tierra en la base del sistema de coordenadas polares.
Problema 13:
La función de movimiento de una partícula está dada
paramétricamente por:
a) Escribir los vectores  ,
, 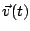 y
y
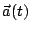 .
.
b) Interprete el significado físico de las
constantes 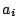 y
y 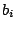 .
.
Suponga en particular:
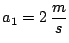 ,
,
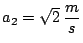 ,
,
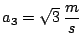 ,
y
,
y
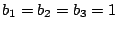 m.
m.
c) Grafique la trayectoria.
d) Calcule el módulo de 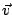 .
.
e) Verifique que los puntos (cuyas coordenadas
están expresadas en metros): 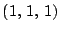 ;
;
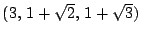 ; y
; y
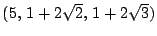 ,
pertenecen a la trayectoria de la partícula. ¿En qué instantes
de tiempo la partícula se encuentra en dichas posiciones?
,
pertenecen a la trayectoria de la partícula. ¿En qué instantes
de tiempo la partícula se encuentra en dichas posiciones?
f) Calcule las distancias que separan los puntos del
item anterior. Relacione estas distancias con los tiempos empleados
en recorrerlas.
Fa.M.A.F ©2003
Pedro Pury
2004-03-19
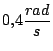 , por cada segundo. Dicha corona
transmite su movimiento a un piñon de
, por cada segundo. Dicha corona
transmite su movimiento a un piñon de