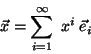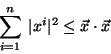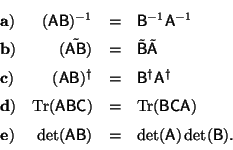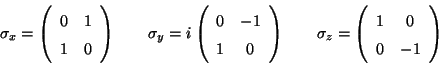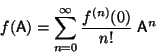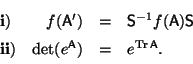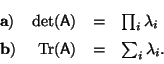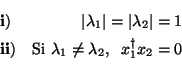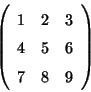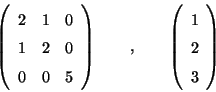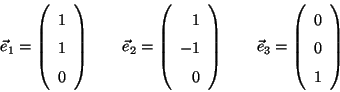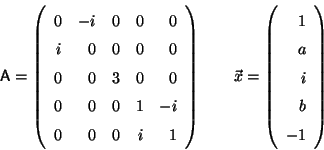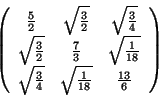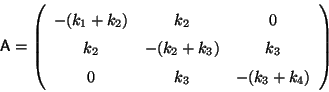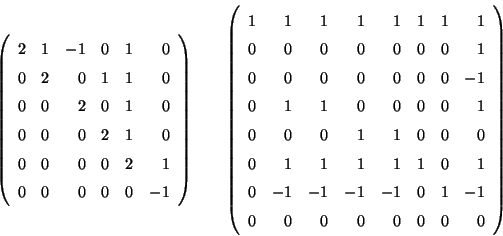Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Métodos Matemáticos de la Física
Guía N 1: Álgebra Lineal
1: Álgebra Lineal
Problema 1: Sean 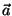 y
y 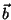 dos vectores
arbitrarios en un espacio vectorial con producto interno. Demuestre
la desigualdad de Cauchy-Schwartz:
dos vectores
arbitrarios en un espacio vectorial con producto interno. Demuestre
la desigualdad de Cauchy-Schwartz:
Determine cuando es válida la igualdad.
Ayuda: Utilice el vector:
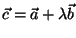 y exija que
y exija que
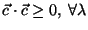 .
Considere una base ortonormal
.
Considere una base ortonormal
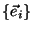 en
un espacio vectorial de dimensión infinita. Por cuestiones de
convergencia, el desarrollo de un vector arbitrario en términos
de la base:
en
un espacio vectorial de dimensión infinita. Por cuestiones de
convergencia, el desarrollo de un vector arbitrario en términos
de la base:
puede carecer de significado. No obstante, utilizando la desigualdad
de Cauchy-Schwartz, demuestre la desigualdad de Bessel:
resultado que es válido para todo 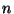 , por grande que este sea.
, por grande que este sea.
Problema 2: Siendo 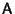 ,
, 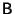 y
y
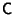 matrices cuadradas, probar que:
matrices cuadradas, probar que:
Problema 3: Supongamos que las matrices A y
B son hermiteanas y las matrices C y D son
unitarias. Demostrar que:
Problema 4: Sea
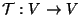 la
transformación lineal dada por
la
transformación lineal dada por
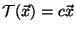 , donde
, donde
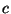 es un escalar fijo. Demostrar que
es un escalar fijo. Demostrar que 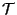 es unitaria si y
sólo si
es unitaria si y
sólo si 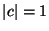 .
Si
.
Si 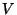 es un espacio unidimensional, demostrar que las únicas
transformaciones unitarias en
es un espacio unidimensional, demostrar que las únicas
transformaciones unitarias en 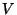 son las descriptas anteriormente.
En particular, si
son las descriptas anteriormente.
En particular, si 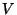 es un espacio real unidimensional, existen
sólo dos transformaciones ortogonales,
es un espacio real unidimensional, existen
sólo dos transformaciones ortogonales,
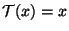 y
y
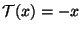 .
.
Problema 5: Las siguientes matrices 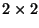 en
en
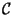 :
:
son las matrices de Pauli. Probar que:
a)
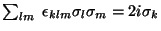 .
Es decir que puede utilizarse la notación:
.
Es decir que puede utilizarse la notación:
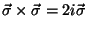 , con
, con
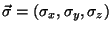 .
.
b)
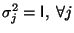 ; donde
I es la matriz identidad.
; donde
I es la matriz identidad.
c) El conjunto de matrices de Pauli mas I
forman una base para el espacio de matrices 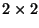 .
.
Problema 6: Dada la transformación de semejanza
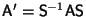 , probar que:
, probar que:
Dada una función analítica 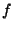 , es usual utilizar la notación
, es usual utilizar la notación
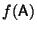 , donde
, donde 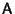 es una matriz cuadrada, para
representar al desarrollo en serie de Taylor de
es una matriz cuadrada, para
representar al desarrollo en serie de Taylor de 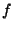 ``evaluado'' en
``evaluado'' en
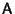 :
:
Utilizando esta notación pruebe que:
Problema 7: Si los autovectores 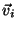 ,
correspondientes a los autovalores
,
correspondientes a los autovalores 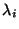 , de la matriz A
forman una base, probar que:
, de la matriz A
forman una base, probar que:
Problema 8: Sea 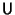 una matriz unitaria y
una matriz unitaria y
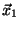 ,
, 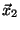 dos vectores propios de
dos vectores propios de 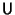 pertenecientes a los autovalores
pertenecientes a los autovalores 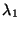 ,
, 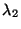 ,
respectivamente. Demostrar que:
,
respectivamente. Demostrar que:
Problema 9: Encontrar los autovalores y autovectores
normalizados de la matriz:
Problema 10: En una dada base
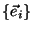 de un espacio vectorial abstracto, una transformación
lineal y un dado vector de dicho espacio, quedan respectivamente
determinados por:
de un espacio vectorial abstracto, una transformación
lineal y un dado vector de dicho espacio, quedan respectivamente
determinados por:
Encontrar las representaciones matriciales de la transformación y
del vector en una nueva base tal que la antigua queda representada
por:
Problema 11: Escribir la matriz A y el vector
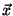 en la base en la cual A es diagonal.
en la base en la cual A es diagonal.
Problema 12: Demostrar cada una de las siguientes
proposiciones relativas a una matriz 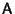 ,
, 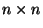 , real
y ortogonal:
, real
y ortogonal:
a) Si 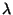 es un autovalor real de
es un autovalor real de 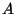 , entonces
, entonces
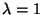 o
o 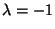 .
.
b) Si 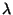 es un autovalor complejo de
es un autovalor complejo de 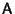 , el complejo conjugado
, el complejo conjugado 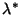 también es autovalor de
también es autovalor de
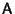 .
Es decir, los autovalores de
.
Es decir, los autovalores de 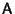 no reales son
conjugados a pares.
no reales son
conjugados a pares.
c) Si 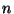 es impar,
es impar, 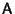 tiene por lo menos un
autovalor real.
tiene por lo menos un
autovalor real.
Problema 13: Sea 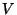 un espacio euclídeo real de
dimensión
un espacio euclídeo real de
dimensión 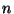 . Una transformación ortogonal
. Una transformación ortogonal
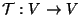 con determinante igual a
con determinante igual a 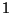 se llama rotación. Si
se llama rotación. Si 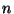 es impar
demostrar que 1 es autovalor para
es impar
demostrar que 1 es autovalor para 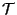 . Esto prueba que toda
rotación de un espacio de dimensión impar tiene un eje fijo.
. Esto prueba que toda
rotación de un espacio de dimensión impar tiene un eje fijo.
Problema 14: Las cónicas con centro en el origen de
un sistema coordenado obedecen la ecuación:
a) Escribir la ecuación en forma matricial:
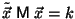 .
.
b) Encuentre la transformación que diagonaliza
M e interprete geométricamente.
c) Ejemplifique con
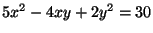 .
.
Problema 15: El tensor de inercia de un cuerpo
rígido en un particular sistema de coordenadas está expresado
por la matriz:
Encuentre los momentos principales de inercia y las direcciones de
los ejes principales. Recuerde que en un sistema coordenado orientado
en la dirección de los ejes principales la matriz asociada al
tensor es diagonal.
Problema 16: Demostrar que las oscilaciones
unidimensionales del sistema mecánico de la figura están regidas
por la ecuación vectorial:
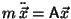 ;
donde:
;
donde:
a) Resolver la ecuación mediante la substitución
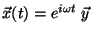 , demostrando que esto
conduce a un problema de autovalores.
, demostrando que esto
conduce a un problema de autovalores.
b) Suponiendo que
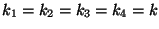 encontrar las
frecuencias de los modos normales de oscilación.
encontrar las
frecuencias de los modos normales de oscilación.
c) Escribir la solución de la ecuación bajo las
condiciones iniciales:
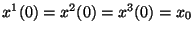 y
y
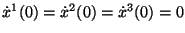 .
.
Problema 17: Si 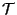 es un operador lineal sobre
un espacio vectorial de dimensión finita, diagonalizable,
probar el teorema de Cayley-Hamilton: Si
es un operador lineal sobre
un espacio vectorial de dimensión finita, diagonalizable,
probar el teorema de Cayley-Hamilton: Si 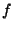 es el polinomio
característico de
es el polinomio
característico de 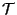 entonces
entonces
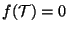 .
Ayuda: Probar que dado un autovector
.
Ayuda: Probar que dado un autovector 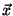 de
de
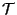 de autovalor
de autovalor 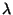 , para todo polinomio
, para todo polinomio 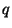 se cumple:
se cumple:
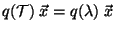 .
.
Problema 18: Una transformación lineal 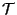 se
llama nilpotente si para algún número natural
se
llama nilpotente si para algún número natural 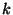 se cumple
que
se cumple
que
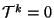 . Probar:
. Probar:
a) Si 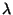 es un autovalor de
es un autovalor de 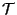 entonces
entonces 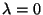 .
.
b) 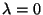 es un autovalor de
es un autovalor de 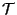 .
.
Se concluye entonces que el conjunto de autovalores de un
operador nilpotente es exactamente
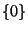 .
.
Problema 19: Sea
 . Considere sobre este
espacio el operador lineal derivación D.
. Considere sobre este
espacio el operador lineal derivación D.
a) Probar que D es nilpotente.
b) Construya la forma de Jordan correspondiente a D.
Problema 20: Si A es una matriz 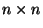 cuyo polinomio característico resulta:
cuyo polinomio característico resulta:
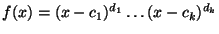 con
con
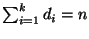 .
¿Cual es la traza de A?
.
¿Cual es la traza de A?
Problema 21: Sea A una matriz triangular
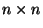 tal que
tal que
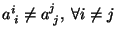 .
Escribir la forma de Jordan asociada con A.
.
Escribir la forma de Jordan asociada con A.
Problema 22: Escribir las formas de Jordan de las
siguientes matrices:
Fa.M.A.F ©1995
Pedro Pury
2001-02-07