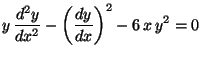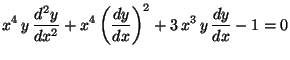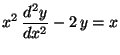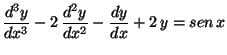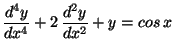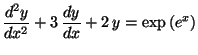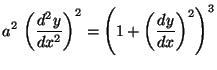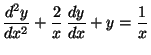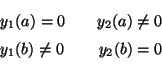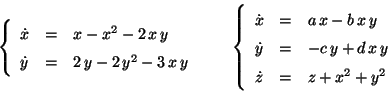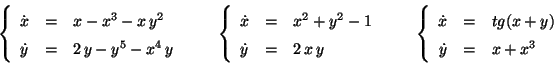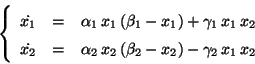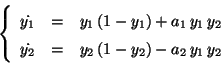Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Métodos Matemáticos de la Física
Guía N 3: Ecuaciones Diferenciales Ordinarias
3: Ecuaciones Diferenciales Ordinarias
Parte I: Soluciones por Cuadraturas
Problema 1: Verifique que las siguientes ecuaciones
diferenciales se reducen a ecuaciones diferenciales de variables
separables:
a)
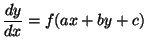 donde
donde 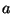 ,
, 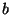 , y
, y 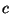 son constantes.
son constantes.
b)
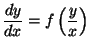
c)
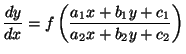
Problema 2: Calcular las soluciones particulares de
las siguientes ecuaciones diferenciales de variables separables, que
satisfacen las condiciones especificadas:
a)
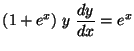 ;
;
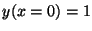 .
.
b)
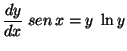 ;
(i)
;
(i)
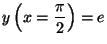 ,
(ii)
,
(ii)
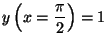 .
.
c)
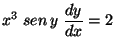 ;
;
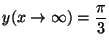 .
.
Problema 3: Calcular la solución general de las
siguientes ecuaciones diferenciales reducibles a ecuaciones
diferenciales homogéneas:
a)
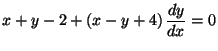 .
.
b)
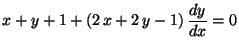 .
.
c)
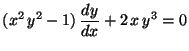 ,
(Ayuda: Utilizar el cambio de variable
,
(Ayuda: Utilizar el cambio de variable
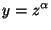 ).
).
Problema 4: Resolver las siguientes ecuaciones
diferenciales utilizando la sustitución:
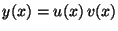 ,
,
a)
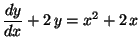 (Ecuación lineal inhomogénea).
(Ecuación lineal inhomogénea).
b)
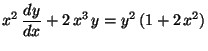 (Ecuación de Bernoulli).
(Ecuación de Bernoulli).
Problema 5: Resolver las siguientes ecuaciones
diferenciales teniendo en cuenta si son diferenciales exactas o bien
si existe un factor integrante:
a)
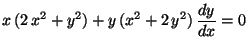 .
.
b)
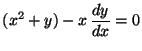 .
.
c)
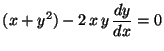 .
.
Problema 6: Determine todas las curvas del plano tales
que toda recta tangente a cada curva forma siempre con los ejes
coordenados un triángulo de area 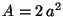 , siendo
, siendo 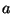 una
constante.
una
constante.
Problema 7: Calcular la solución general de las
siguientes ecuaciones diferenciales ordinarias:
a)
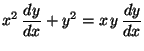
b)
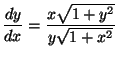
c)
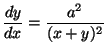
d)
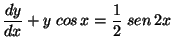
e)
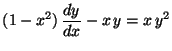
f)
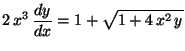
g)
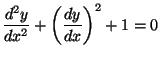
h)
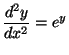
i)
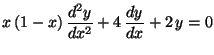
j)
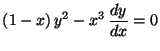
k)
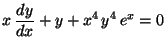
l)
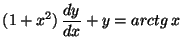
m)
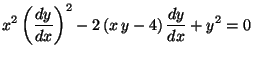 (soluciones general y singular)
(soluciones general y singular)
n)
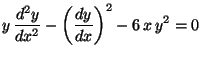
o)
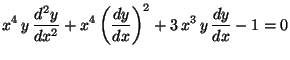
p)
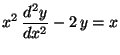
q)
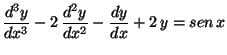
r)
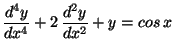
s)
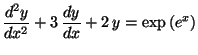
t)
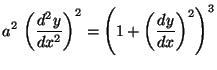
u)
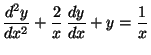
Problema 8: En la activación de una lámina de
Indio por un flujo constante de neutrones, el número 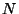 de
átomos radiactivos obedece la ecuación:
de
átomos radiactivos obedece la ecuación:
donde 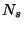 es el número constante que se alcanza luego de la
``saturación''. Calcular
es el número constante que se alcanza luego de la
``saturación''. Calcular 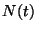 si
si 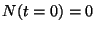 .
.
Problema 9: Encontrar la solución general de:
donde 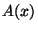 es una fiunción conocida e
es una fiunción conocida e 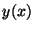 es la incógnita.
es la incógnita.
Problema 10: Calcular la solución general de la
ecuación:
Ayuda: Eliminar el término en derivada primera.
Problema 11: Notar que: 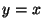 es una solución de
la ecuación:
es una solución de
la ecuación:
si el segundo miembro se iguala a cero. Use este hecho para obtener
la solución general de la ecuación dada.
Problema 12: Considere la ecuación diferencial:
en el intervalo
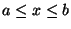 . Suponga que se conocen dos
soluciones,
. Suponga que se conocen dos
soluciones, 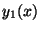 e
e 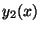 , tales que:
, tales que:
Dar la solución de la ecuación:
que obedece las condiciones 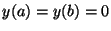 , en la forma:
, en la forma:
donde 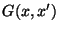 , la llamada función de Green, se construye sólo
en términos de las soluciones
, la llamada función de Green, se construye sólo
en términos de las soluciones 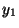 e
e 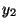 y asume diferentes
formas funcionales para
y asume diferentes
formas funcionales para 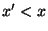 y
y 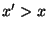 .
Ilustrar este problema resolviendo:
.
Ilustrar este problema resolviendo:
Parte II: Soluciones en Series de Potencias
Problema 13: Considere la ecuación diferencial:
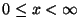 , donde
, donde 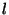 es un entero no negativo.
Encontrar todos los valores de la constante
es un entero no negativo.
Encontrar todos los valores de la constante 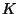 los cuales
generan soluciones finitas en todo el rango de
los cuales
generan soluciones finitas en todo el rango de 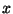 . Una ecuación
como esta se obtiene al resolver la ecuación de Schrödinger para
el átomo de Hidrógeno.
. Una ecuación
como esta se obtiene al resolver la ecuación de Schrödinger para
el átomo de Hidrógeno.
Problema 14: ¿Para que valores de la constante 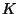 la
ecuación diferencial:
la
ecuación diferencial:
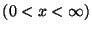 tiene una solución no trivial que se anula para
tiene una solución no trivial que se anula para
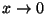 y
y
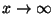 ?
?
Problema 15: ¿Para que valores de la constante 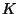 la
ecuación diferencial:
la
ecuación diferencial:
posee una solución acotada en el rango
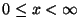 ?
?
Problema 16: Se desea una solución de la ecuación
diferencial:
tal que 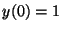 ,
, 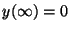 . ¿Para que valores de
. ¿Para que valores de 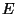 es
esto posible?
es
esto posible?
Problema 17: La ecuación de Bessel para 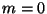 es:
es:
Una solución de esta ecuación es:
Mostrar que existe una segunda solución de la forma:
y encuentre los tres primeros coeficientes 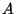 ,
, 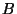 ,
, 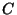 .
.
Problema 18: Considere la ecuación diferencial:
Dar dos soluciones, una regular y de valor 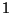 en el origen y la otra
de la forma:
en el origen y la otra
de la forma:
donde 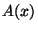 y
y 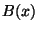 son regulares en el origen. Dar los primeros
tres términos de los desarrollos en serie de
son regulares en el origen. Dar los primeros
tres términos de los desarrollos en serie de 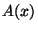 y
y 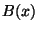 .
.
Parte III: Sistemas de Ecuaciones Diferenciales
Problema 19: Encontrar los todos los puntos de
equilibrio de los siguientes sistemas de ecuaciones diferenciales:
Problema 20: Considere el sistema de ecuaciones
diferenciales:
a) Mostrar que 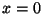 ,
, 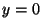 es el único punto de
equilibrio si:
es el único punto de
equilibrio si:
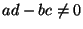 .
.
b) Mostrar que el sistema posee una línea de
puntos de equilibrio si: 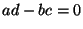 .
.
Problema 21: Encuentre las soluciones de equilibrio de
los siguientes sistemas de ecuaciones diferenciales y determine si
son estables o inestables:
Problema 22: Considere un sistema presa-predador donde
el predador posee un medio alternativo de sustento. Este sistema
puede ser modelado por el sistema de ecuaciones diferenciales:
donde 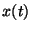 e
e 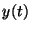 son las poblaciones al tiempo
son las poblaciones al tiempo 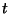 de predadores
y presas respectivamente y
de predadores
y presas respectivamente y 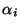 ,
, 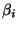 y
y 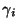 son
constantes.
son
constantes.
a) Mostrar que el cambio de coordenadas
reduce el sistema de ecuaciones a:
donde
b) ¿Cuales son las poblaciones de equilibrio estables
cuando: (i) 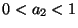 , (ii)
, (ii) 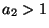 ?
?
c) Se observa que 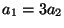 (
(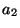 es una medida
de la agresividad del predador). ¿Cuál es el valor de
es una medida
de la agresividad del predador). ¿Cuál es el valor de 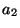 si el
instinto del predador consiste en maximizar su población de
equilibrio estable?
si el
instinto del predador consiste en maximizar su población de
equilibrio estable?
Fa.M.A.F ©1995
Pedro Pury
2001-02-07
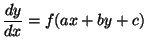 donde
donde 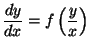
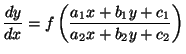
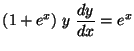 ;
;
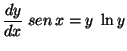 ;
(i)
;
(i)
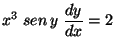 ;
;
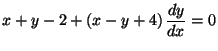 .
.
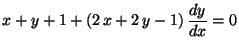 .
.
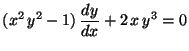 ,
(Ayuda: Utilizar el cambio de variable
,
(Ayuda: Utilizar el cambio de variable
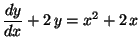 (Ecuación lineal inhomogénea).
(Ecuación lineal inhomogénea).
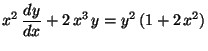 (Ecuación de Bernoulli).
(Ecuación de Bernoulli).
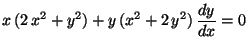 .
.
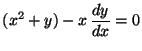 .
.
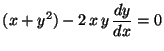 .
.
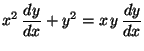
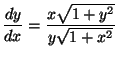
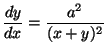
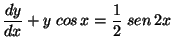
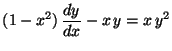
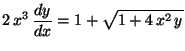
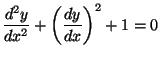
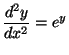
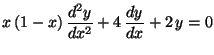
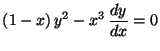
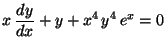
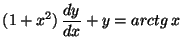
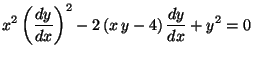 (soluciones general y singular)
(soluciones general y singular)