Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Práctico Especial 2002: I.
Problema de Simulación con Opciones
 Introducción a las Opciones
Introducción a las Opciones
Una opción otorga el derecho, sin generar la obligación a su
tenedor, de comprar o vender un activo financiero (por ejemplo una
acción, un bono, un commodity, monedas, etc.) bajo términos
específicos. Una opción ``call'' es aquella que da el derecho
de comprar y una opción ``put'' es una que da el derecho de vender
una acción. Ambos tipos de opciones tienen un precio estipulado
por acción o ``strike'' para la operación de compra o venta y un
tiempo de ejercicio explícito. Además, existen dos condiciones
estándar bajo las cuales operan las opciones: Opciones ``Europeas''
son aquellas que sólo pueden realizarse al cabo del tiempo de
ejercicio, mientras que las opciones ``Americanas'' pueden utilizarse
en cualquier momento hasta el tiempo de ejercicio. De esta manera,
una opción ``call'' Europea con precio ``strike'' 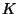 y tiempo de
ejercicio
y tiempo de
ejercicio 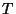 le otorga a su poseedor el derecho de comprar al tiempo
le otorga a su poseedor el derecho de comprar al tiempo
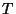 una acción al precio
una acción al precio 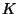 , mientras que una opción ``put''
Americana da a su tenedor el derecho de realizar la venta de una
acción en cualquier instante de tiempo
, mientras que una opción ``put''
Americana da a su tenedor el derecho de realizar la venta de una
acción en cualquier instante de tiempo 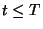 por el precio
``strike''. Las opciones permiten a los inversiores manejar el
riesgo de una cartera de acciones, pero lógicamemnte tienen un
costo. Este último es en definitiva el riesgo de pérdida que
asume el invesor tenedor de la opción.
por el precio
``strike''. Las opciones permiten a los inversiores manejar el
riesgo de una cartera de acciones, pero lógicamemnte tienen un
costo. Este último es en definitiva el riesgo de pérdida que
asume el invesor tenedor de la opción.
Aquí
puede encontrarse una introducción al tema de las opciones.
 Movimiento Browniano Geométrico
Movimiento Browniano Geométrico
Un modelo usual para simular la evolución del precio de
una acción en el tiempo es el llamado movimiento Browniano
geométrico.
Este proceso asume que si 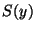 es el precio de la acción en el
tiempo
es el precio de la acción en el
tiempo 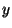 , entonces el cociente entre precio de la acción en un
futuro instante de tiempo
, entonces el cociente entre precio de la acción en un
futuro instante de tiempo 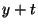 y
y 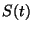 es una variable aleatoria
lognormal, independientemente de la historia de los
precios trancurrida hasta el instante
es una variable aleatoria
lognormal, independientemente de la historia de los
precios trancurrida hasta el instante 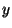 . Esto es, dado
. Esto es, dado 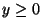
es una variable aletoria normal con media 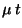 y varianza
y varianza
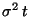 .
.
Ejercicio 1: Una variable aleatoria 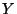 se llama lognormal con
parámetros
se llama lognormal con
parámetros 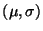 , si
, si 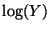 es una variable aleatoria
normal com media
es una variable aleatoria
normal com media 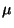 y varianza
y varianza 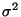 .
.
a) Demostrar que:
![$E[Y] = \exp \left( \mu + \displaystyle\frac{\sigma^2}{2} \right)$](img18.gif) .
.
b) Calcular Var![$[Y]$](img19.gif) .
.
Ejercicio 2: Construir un generador para la variable aletoria 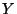 lognormal con parámetros
lognormal con parámetros 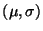 .
Implementar el algoritmo en la computadora y estimar
.
Implementar el algoritmo en la computadora y estimar
![$E[Y]$](img20.gif) y Var
y Var![$[Y]$](img19.gif) . Asumir los valores
. Asumir los valores 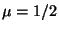 ,
, 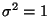 ,
y construir una tabla con las estimaciones de los valores pedidos
para
,
y construir una tabla con las estimaciones de los valores pedidos
para 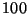 ,
, 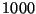 ,
, 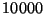 ,
, 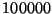 y
y 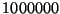 simulaciones.
simulaciones.
Una variable aletoria normal puede tomar valores positivos o
negativos con igual probabilidad. El movimiento Browniano
geométrico, dado que considera que el ``logaritmo'' del cociente
de precios es una variable normal, garantiza que los precios
sólo puedan tomar valores positivos. Además al ser las razones
de precios, separados por un período de tiempo fijo 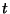 , las
que tienen distribución normal, resulta que el porcentaje
de cambio en el precio no depende del precio actual
, las
que tienen distribución normal, resulta que el porcentaje
de cambio en el precio no depende del precio actual 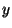 ,
pero los cambios de precio absolutos si resultan ser
proporcionales al precio de referencia:
,
pero los cambios de precio absolutos si resultan ser
proporcionales al precio de referencia:
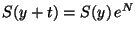 ,
donde
,
donde 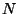 es una variable aleatoria normal de parámetros
es una variable aleatoria normal de parámetros
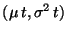 . Sin embargo, debe notarse que si los
parámetros del modelo
. Sin embargo, debe notarse que si los
parámetros del modelo 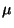 y
y 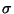 están determinados,
ninguna otra información es necesaria para determinar los precios
futuros a partir del precio presente; la información sobre los
precios pasados es irrelevante. Es precisamente este hecho, el que
limita la aplicación del movimiento Browniano geométrico en
situciones prácticas reales.
están determinados,
ninguna otra información es necesaria para determinar los precios
futuros a partir del precio presente; la información sobre los
precios pasados es irrelevante. Es precisamente este hecho, el que
limita la aplicación del movimiento Browniano geométrico en
situciones prácticas reales.
Ejercicio 3: Considerar un movimiento Browniano geométrico con
parámetros 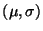 . Sea
. Sea 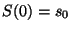 el valor inicial
del proceso.
el valor inicial
del proceso.
a) Mostrar que:
![$E[S(t)] = \exp
\left[ t\left( \mu + \displaystyle\frac{\sigma^2}{2} \right)\right]$](img34.gif) .
.
b) Calcular Var![$[S(t)]$](img35.gif) .
.
Ejercicio 4: Construir un generador para el movimiento Browniano
geométrico 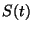 con parámetros
con parámetros 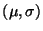 .
Para tiempos discretos se tiene que
.
Para tiempos discretos se tiene que
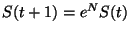 ,
donde
,
donde 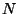 es una variable aleatoria normal de parámetros
es una variable aleatoria normal de parámetros
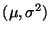 .
Implementar el algoritmo en la computadora y graficar dos
realizaciones del proceso (los 100 primeros pasos)
correspondientes a los valores de los parámetros:
(
.
Implementar el algoritmo en la computadora y graficar dos
realizaciones del proceso (los 100 primeros pasos)
correspondientes a los valores de los parámetros:
(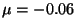 ,
,
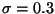 ) y (
) y (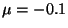 ,
,
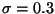 )
y considerando
)
y considerando 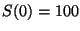 . Utilizar para ambas realizaciones del
proceso la misma semilla en el generador de números aleatorios.
. Utilizar para ambas realizaciones del
proceso la misma semilla en el generador de números aleatorios.
 Arbitraje
Arbitraje
Un esquema de apuestas, que involucra la compra y/o venta de
acciones y opciones, que da lugar a una ganancia segura se
denomina arbitraje. Los costos de las opciones se fijan
de manera de eliminar el arbitraje. Bajo la hipótesis de que los
precios de las acciones siguen un movimiento Browniano geométrico,
Black y Scholes dedujeron el 1973 una fórmula para fijar el precio
de las opciones ``call'', asociadas a una dada acción, de forma de
evitar el arbitraje. La fórmula de Black-Scholes fija el costo 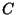 de la opción ``call'' en función del tiempo y depende de la tasa
de interés del mercado
de la opción ``call'' en función del tiempo y depende de la tasa
de interés del mercado 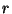 , el precio inicial de la acción
, el precio inicial de la acción
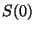 , el precio de ejercicio de la opción
, el precio de ejercicio de la opción 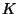 y del parámetro
y del parámetro
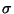 del movimiento Browniano geométrico (llamado tambien
parámetro de volatilidad), pero no depende del parámetro
del movimiento Browniano geométrico (llamado tambien
parámetro de volatilidad), pero no depende del parámetro 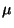 .
La fórmula de Black-Scholes, cuya demostración excede las
intenciones del práctico, establece que:
.
La fórmula de Black-Scholes, cuya demostración excede las
intenciones del práctico, establece que:
donde
y 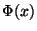 es la distribución de probabilidad acumulada de la
variable normal estándar.
Naturalmente, en el lanzamiento de la opción (
es la distribución de probabilidad acumulada de la
variable normal estándar.
Naturalmente, en el lanzamiento de la opción (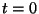 ) se tiene que
) se tiene que
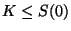 , siendo la igualdad el caso habitual.
Los valores límites del costo de la opción, que resultan de
la expresión dada, son:
, siendo la igualdad el caso habitual.
Los valores límites del costo de la opción, que resultan de
la expresión dada, son:
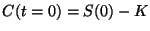 y
y
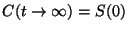 .
.
Ejercicio 5: La función error, 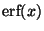 ,
se define según:
,
se define según:
a) Mostrar que:
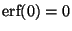 ,
,
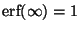 y
y
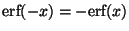 .
.
b) Escribir 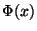 , la distribución de
probabilidad acumulada de la variable normal estándar,
en función de
, la distribución de
probabilidad acumulada de la variable normal estándar,
en función de 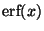 , para todo valor de
, para todo valor de 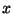 .
.
c) Desarrollar una rutina en computadora para evaluar
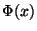 utilizando la rutina del ``Numerical Recipes'' diseñada
para el cálculo de
utilizando la rutina del ``Numerical Recipes'' diseñada
para el cálculo de 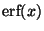 .
.
 Estrategia para Opciones ``Call'' Americanas
Estrategia para Opciones ``Call'' Americanas
La condición obvia para realizar una opción ``call'', en un dado
instante 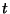 , es
, es 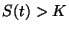 . De esta forma, el tenedor de la opción
compra la acción por el precio
. De esta forma, el tenedor de la opción
compra la acción por el precio 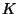 establecido en la opción y
acto seguido la vende por su precio de mercado
establecido en la opción y
acto seguido la vende por su precio de mercado 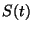 , realizando de
esta manera una ganancia igual
, realizando de
esta manera una ganancia igual 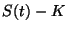 . Ahora bien, no es obvio
responder en que instante de tiempo conviene realizar la opción (en
el caso de una opción americana) para obtener la máxima ganancia.
Una estrategia que se utiliza para estimar el momento más apropiado
para realizar la opción, es explorar la posibilidad de arbitraje a
partir de la fórmula de Black-Scholes. Esta política de compra
puede resumirse de la siguiente manera:
. Ahora bien, no es obvio
responder en que instante de tiempo conviene realizar la opción (en
el caso de una opción americana) para obtener la máxima ganancia.
Una estrategia que se utiliza para estimar el momento más apropiado
para realizar la opción, es explorar la posibilidad de arbitraje a
partir de la fórmula de Black-Scholes. Esta política de compra
puede resumirse de la siguiente manera:
La opción ``call'' se ejerce faltando 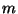 días para que
expire su tiempo de ejercicio si se cumple que:
días para que
expire su tiempo de ejercicio si se cumple que:
i) 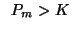 ,
,
ii)
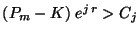 , para cada
, para cada
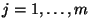 ;
;
donde 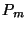 es el precio de mercado de la acción faltando
es el precio de mercado de la acción faltando
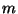 días por transcurrir para que expire la opción
(
días por transcurrir para que expire la opción
(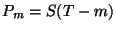 ),
), 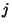 es el número de días contados desde el
momento en que se ejerce la opción. La condición (ii)
explora si el valor de la ganancia realizada:
es el número de días contados desde el
momento en que se ejerce la opción. La condición (ii)
explora si el valor de la ganancia realizada: 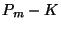 (cuando esta
ocurre según la condición (i)), actualizada a la tasa de
interés (continua)
(cuando esta
ocurre según la condición (i)), actualizada a la tasa de
interés (continua) 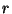 del mercado, resulta mayor que el costo de
la opción en cada uno de los días subsiguientes hasta que
expira la opción. Si para algún
del mercado, resulta mayor que el costo de
la opción en cada uno de los días subsiguientes hasta que
expira la opción. Si para algún 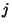 no se cumple la condición
(ii) no conviene realizar la opción, porque el costo de esta
el día
no se cumple la condición
(ii) no conviene realizar la opción, porque el costo de esta
el día 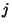 resultará mayor que el valor actualizado de la
ganancia obtenida al realizarla. Claramente, según esta
estrategia si al cabo de los
resultará mayor que el valor actualizado de la
ganancia obtenida al realizarla. Claramente, según esta
estrategia si al cabo de los 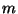 días no se realiza la
opción la ganancia obtenida es nula.
días no se realiza la
opción la ganancia obtenida es nula.
Ejercicio 6: Suponiendo que se tiene una opción ``call'' americana
que expira dentro de 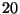 días (es decir que aún restan por
transcurrir
días (es decir que aún restan por
transcurrir 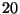 días de posibles transacciones) y siendo
días de posibles transacciones) y siendo
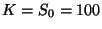 , estimar mediante simulación el valor esperado y la
desviación estándar de la ganancia obtenida si se realiza la
opción según la estrategia anteriormente detallada. Comparar
los valores del promedio y desviación estándar obtenidos para
la ganancia, con los que resultan de operar bajo las mismas
circunstancias según la estrategia: Esperar hasta el último
día para realizar la opción, y realizarla si
, estimar mediante simulación el valor esperado y la
desviación estándar de la ganancia obtenida si se realiza la
opción según la estrategia anteriormente detallada. Comparar
los valores del promedio y desviación estándar obtenidos para
la ganancia, con los que resultan de operar bajo las mismas
circunstancias según la estrategia: Esperar hasta el último
día para realizar la opción, y realizarla si 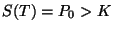 .
.
Observaciones:
Efectuar las estimaciones solicitadas mediante 10000 simulaciones
y teniendo en cuenta las siguientes ``condiciones de mercado'':
a) 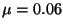 ,
, 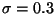 ,
, 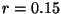 ,
,
b) 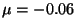 ,
, 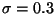 ,
, 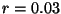 ,
,
c) 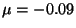 ,
, 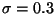 ,
, 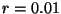 ,
,
d) 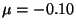 ,
, 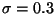 ,
, 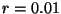 .
.
Fa.M.A.F ©2002
Pedro Pury
2002-05-07
![$E[Y] = \exp \left( \mu + \displaystyle\frac{\sigma^2}{2} \right)$](img18.gif) .
.
![$E[S(t)] = \exp
\left[ t\left( \mu + \displaystyle\frac{\sigma^2}{2} \right)\right]$](img34.gif) .
.