Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Guía N 1: Introducción
1: Introducción
Problema 1:
Los siguientes datos corresponden a los tiempos de llegada y de
servicio que se invierten en cada uno de los primeros 13 clientes
que llegan a un sistema con un único servidor:
| Tiempo de llegada: |
12 |
31 |
63 |
95 |
99 |
154 |
198 |
221 |
304 |
346 |
411 |
455 |
537 |
| Tiempo de servicio: |
40 |
32 |
55 |
48 |
18 |
50 |
47 |
18 |
28 |
54 |
40 |
72 |
12 |
El sistema funciona de manera tal que a llegar un cliente, pasa a
servicio si el servidor está libre o bien se forma en la línea
de espera. Cuando el servidor concluye el trabajo de un cliente, el
siguiente de la línea, es decir quien ha esperado más tiempo,
entra en servicio.
a) Determine los tiempos de salida y de espera de
estos primeros 13 clientes.
b) Repita lo calculado en el item a) considerando
que el sistema posee dos servidores que atienden clientes.
c) Repita lo calculado en el item a) considerando
un único servidor pero bajo la condición, que cuando el servidor
concluye un servicio, el siguiente cliente debe ser el que haya
esperado menos tiempo.
Problema 2: Considere un sistema con un único servidor en el que los
clientes son atendidos por orden de llegada.. Sean 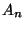 ,
, 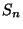 y
y 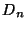 , respectivamente, la hora de llegada, el tiempo de servicio y
la hora de salida del cliente
, respectivamente, la hora de llegada, el tiempo de servicio y
la hora de salida del cliente 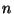 .
.
a) Asumiendo 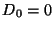 , mostrar que para
, mostrar que para 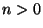
b) Determinar la fórmula de recurrencia para un
sistema con dos servidores.
c) Generalizar la fórmula de recurrencia para un
sistema con 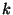 servidores.
servidores.
d) Implementar un programa en computadora que calcule
las horas de salida y tiempos de espera en función de las horas de
llegada y los tiempos de servicio de los clientes. Verificar lo
calculado en los items a) y b) del problema anterior.
Problema 3: La variable aleatoria 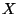 toma valores en el conjunto
toma valores en el conjunto
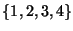 con la siguiente probabilidad:
con la siguiente probabilidad:
a) Determinar el valor de 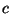 .
.
b) Calcular
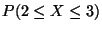 .
.
c) Calcular ![$E[X]$](img15.gif) .
.
Problema 4: Mostrar que
![$\mbox{Var}[a \,X + b] = a^2 \,\mbox{Var}[X]$](img16.gif) .
.
Problema 5: Suponga que los motores de aviación, independientemente
de sus características y potencia, tienen una probabilidad 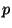 de funcionar sin fallas durante el tiempo que insume un vuelo
transatlántico. Suponga además que un avión necesita al menos
la mitad de sus motores funcionando sin fallas para poder volar.
Sea
de funcionar sin fallas durante el tiempo que insume un vuelo
transatlántico. Suponga además que un avión necesita al menos
la mitad de sus motores funcionando sin fallas para poder volar.
Sea 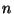 el número de motores de un avión.
el número de motores de un avión.
a) Si 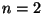 , calcule la probabilidad
, calcule la probabilidad 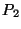 que un
avión complete el vuelo.
que un
avión complete el vuelo.
b) Si 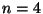 , calcule la probabilidad
, calcule la probabilidad 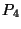 que un
avión complete el vuelo.
que un
avión complete el vuelo.
c) Grafique 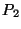 y
y 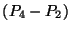 como funciones
de
como funciones
de 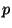 .
.
d) Determine para que valores de 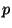 un avión
bimotor tiene más probabilidad de completar el vuelo
transatlántico que un avión cuatrimotor; es decir,
para que valores de
un avión
bimotor tiene más probabilidad de completar el vuelo
transatlántico que un avión cuatrimotor; es decir,
para que valores de 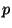 resulta
resulta 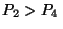 ?
?
Problema 6: Calcular la relación de recurrencia
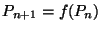 para
la distribución de probabilidad de Poisson. Discutir su uso para un
cálculo numérico eficiente de la distribución de Poisson.
para
la distribución de probabilidad de Poisson. Discutir su uso para un
cálculo numérico eficiente de la distribución de Poisson.
Problema 7: Sean 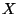 e
e 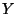 variables aleatorias independientes con
distribución de Poisson con parámetros
variables aleatorias independientes con
distribución de Poisson con parámetros 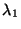 y
y 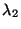 respectivamente. Demostrar que la variable
respectivamente. Demostrar que la variable 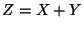 es de Poisson con
parámetro
es de Poisson con
parámetro
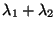 .
.
Problema 8: Sean 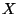 e
e 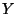 variables aleatorias independientes
distribuídas exponencialmente
variables aleatorias independientes
distribuídas exponencialmente
a) Calcular 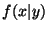 .
.
b) Calcular 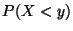 , donde
, donde 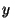 es un valor dado.
es un valor dado.
c) Calcular
![$P(X < Y) \equiv E[P(X < y)] = \,?$](img34.gif)
Problema 9: Sean 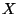 e
e 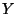 variables aleatorias independientes e
idénticamente distribuídas de forma exponencial. Calcular la
densidad de probabilidad condicional de
variables aleatorias independientes e
idénticamente distribuídas de forma exponencial. Calcular la
densidad de probabilidad condicional de 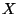 dado que
dado que 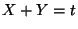 .
.
Problema 10: Una máquina embotelladora de soda inyecta en promedio
una cantidad 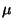 (en moles) de gas carbónico en cada botella.
La cantidad de gas inyectado tiene una distribución normal con
una desviación estándar igual a
(en moles) de gas carbónico en cada botella.
La cantidad de gas inyectado tiene una distribución normal con
una desviación estándar igual a 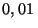 mol. Calcule el valor
de
mol. Calcule el valor
de 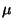 para que solamente en el
para que solamente en el 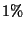 de las botellas resulte
con una cantidad de gas que supere
de las botellas resulte
con una cantidad de gas que supere  mol.
mol.
Fa.M.A.F ©2001-2002
Pedro Pury
2001-03-01