Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Guía N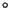 3: Generación de Variables Aleatorias
Discretas
3: Generación de Variables Aleatorias
Discretas
Problema 1: Se baraja un conjunto de 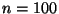 cartas (numeradas
consecutivamente del 1 al 100) y se extrae del mazo una carta por
vez. Consideramos que ocurre un ``éxito'' si la i-ésima carta
extraída es aquella cuyo número es
cartas (numeradas
consecutivamente del 1 al 100) y se extrae del mazo una carta por
vez. Consideramos que ocurre un ``éxito'' si la i-ésima carta
extraída es aquella cuyo número es 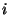 (
(
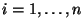 ).
).
a) Escribir un programa de simulación para estimar
la esperanza y la varianza del número total de éxitos.
b) Determine las respuestas exactas para 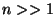 y compárelas con los resultados estimados.
y compárelas con los resultados estimados.
Problema 2: Se desea construir una aproximación de:
a) Determine un algoritmo para estimar la cantidad
deseada.
b) Obtener la aproximación sorteando 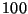 números aleatorios.
números aleatorios.
c) ¿Es buena la aproximación obtenida?
Problema 3: Sea 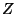 una variable aleatoria normal estándar.
Calcular
una variable aleatoria normal estándar.
Calcular ![$E[\vert Z\vert]$](img9.gif) .
.
Problema 4: Desarrollar dos métodos para generar una variable aleatoria
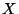 cuya distribución de probabilidad está dada por:
cuya distribución de probabilidad está dada por:
Problema 5: Desarrollar un método para generar una variable aleatoria
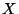 cuya distribución de probabilidad está dada por:
cuya distribución de probabilidad está dada por:
Problema 6: Sea 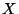 una variable aleatoria cuya distribución de
probabilidad es
una variable aleatoria cuya distribución de
probabilidad es 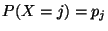 con
con 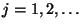 . Sea:
. Sea:
Las cantidades 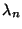 , son las tasas discretas de riesgo.
Considerando a
, son las tasas discretas de riesgo.
Considerando a 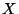 como el tiempo (discreto) de vida de algún
artículo,
como el tiempo (discreto) de vida de algún
artículo, 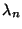 representa la probabilidad de que habiendo
sobrevivido hasta el tiempo
representa la probabilidad de que habiendo
sobrevivido hasta el tiempo 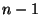 , muera en el tiempo
, muera en el tiempo 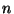 .
.
a) Mostrar que
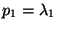 y que
y que
Método de la tasa discreta de riesgo para simular
variables aleatorias discretas: Se genera una sucesión de
números aleatorios que termina cuando el n-ésimo número
generado es menor que 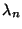 .
El algoritmo puede escribirse como sigue:
.
El algoritmo puede escribirse como sigue:
Paso 1: X = 1
Paso 2: Generar U
Paso 3: Si U < 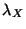 , terminar.
, terminar.
Paso 4: X = X + 1
Paso 5: Ir al Paso 2
b) Mostrar que los valores de 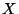 que genera este
proceso tienen la distribución de probabilidad deseada.
que genera este
proceso tienen la distribución de probabilidad deseada.
c) Suponer que 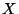 es una variabla aleatoria
geométrica con parámetro
es una variabla aleatoria
geométrica con parámetro 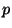 :
:
Determinar los valores de
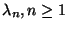 . Explique como
funciona el algoritmo anterior en este caso y por qué es evidente
su validez.
. Explique como
funciona el algoritmo anterior en este caso y por qué es evidente
su validez.
Problema 7: Suponiendo que
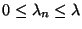 ,
para todo
,
para todo 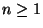 ; considerar el siguiente algoritmo para generar
una variable aleatoria con tasas dicretas de riesgo
; considerar el siguiente algoritmo para generar
una variable aleatoria con tasas dicretas de riesgo
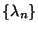 :
:
Paso 1: S = 0
Paso 2: Generar U,
![$Y = \mbox{Ent} \left[
\displaystyle\frac{\log(U)}{\log(1-\lambda)}\right] + 1$](img28.gif)
Paso 3: S = S + Y
Paso 4: Generar U
Paso 5: Si U
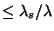 , tomar X = S y
terminar. Caso Contrario, ir a Paso 2.
, tomar X = S y
terminar. Caso Contrario, ir a Paso 2.
a) ¿Cuál es la distribución de 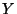 en el paso
en el paso 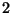 ?
?
b) Explique como funciona el algoritmo.
c) Argumentar que 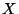 resulta una variable aleatoria
con tasas discretas de riesgo
resulta una variable aleatoria
con tasas discretas de riesgo
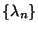 .
.
Fa.M.A.F ©2001-2002
Pedro Pury
2001-03-26

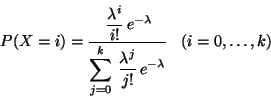
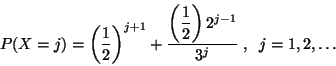
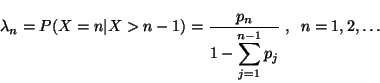
![$Y = \mbox{Ent} \left[
\displaystyle\frac{\log(U)}{\log(1-\lambda)}\right] + 1$](img28.gif)