Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Guía N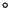 4: Generación de Variables Aleatorias
Continuas
4: Generación de Variables Aleatorias
Continuas
Problema 1: Desarrollar un método para generar una variable aleatoria
cuya densidad de probabilidad es
Problema 2: Desarrollar un método para generar una variable aleatoria
con distribución de probabilidad
Una variable aleatoria con esta distribución se conoce como
variable aleatoria de Weibull.
Problema 3: Método de la composición: Suponer que es
relativamente fácil generar 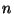 variables aleatorias a partir
de sus distribuciones de probabilidad
variables aleatorias a partir
de sus distribuciones de probabilidad 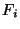 ,
, 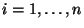 .
Implementar un método para generar una variable aleatoria
cuya distribución de probabilidad es
.
Implementar un método para generar una variable aleatoria
cuya distribución de probabilidad es
donde 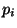 ,
, 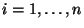 , son números no negativos
cuya suma es 1.
, son números no negativos
cuya suma es 1.
Problema 4: Desarrollar un método para generar la variable aleatoria
con función distribución
Pensar en el método de composición del ejercicio anterior.
En particular, sea 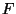 la función de distribución de
la función de distribución de 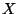 y
suponga que la distribución condicional de
y
suponga que la distribución condicional de 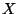 dado
dado 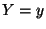 es
es
Problema 5: Considere que es sencillo generar una variable aleatoria a
partir de cualquiera de las distribuciones 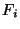 ,
, 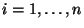 .
Explicar como generar variables aleatorias a partir de las siguientes
distribuciones:
.
Explicar como generar variables aleatorias a partir de las siguientes
distribuciones:
a)
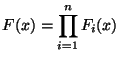 ,
b)
,
b)
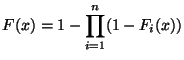
Sugerencia: Si 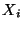 ,
, 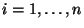 , son variables
aleatorias independientes, donde
, son variables
aleatorias independientes, donde 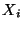 tiene distribución
tiene distribución 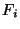 ,
¿cuál variable aleatoria tiene como distribución a
,
¿cuál variable aleatoria tiene como distribución a 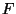 en cada
caso?
en cada
caso?
Problema 6: Utilizar el método del rechazo y los resultados del
ejercicio anterior para desarrollar otros dos métodos, además
del método de la transformada inversa, para generar una variable
aleatoria con distribución de probabilidad
Analizar la eficiencia de los tres métodos para generar la variable
a partir de 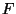 .
.
Problema 7: Desarrollar dos métodos para generar una variable aleatoria
con densidad de probabilidad
Comparar sus eficiencias.
Problema 8: Escribir dos programas para generar un variable aleatoria
normal mediante
a) la generación de variables exponenciales según
el ejemplo 5f del libro Simulación de S. M. Ross,
b) el método polar.
Testear los programas calculando la media y varianza de
10000 valores generados con ambos métodos.
Problema 9: Sea en par 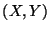 uniformemente distribuído en un
círculo de radio
uniformemente distribuído en un
círculo de radio 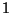 . Mostrar que si
. Mostrar que si 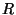 es la distancia del
punto
es la distancia del
punto 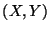 al centro del círculo, entonces
al centro del círculo, entonces 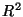 está
uniformemente distribuída en el intervalo
está
uniformemente distribuída en el intervalo 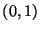 .
.
Problema 10: Escribir un programa para generar las primeras 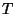 unidades
de tiempo de un proceso de Poisson con parámetro
unidades
de tiempo de un proceso de Poisson con parámetro 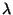 .
.
Problema 11: Los autobuses que llevan los aficionados a un encuentro
deportivo llegan a destino de acuerdo con un proceso de Poisson a razón de cinco por hora.
La capacidad de los autobuses es una variable aleatoria que toma valores en el
conjunto:
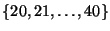 con igual probabilidad.
A su vez, las capacidades de dos autobuses distintos son variables
independientes. Escribir un algoritmo para simular la llegada de
aficionados al encuentro en el instante
con igual probabilidad.
A su vez, las capacidades de dos autobuses distintos son variables
independientes. Escribir un algoritmo para simular la llegada de
aficionados al encuentro en el instante 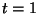 hora.
hora.
Problema 12:
a) Escribir un programa que utilice el algoritmo del
adelgazamiento para generar las primeras diez unidades de tiempo de
un proceso de Poisson no homogéneo con función de intensidad
b) Indicar una forma de mejorar el algoritmo de
adelgazamiento para este ejemplo particular.
Fa.M.A.F ©2001-2002
Pedro Pury
2001-04-10
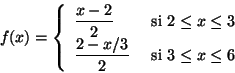
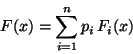
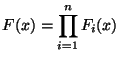 ,
b)
,
b)