Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Modelos y Simulación -
Licenciatura en Computación
Guía N 6:
Técnicas de Validación Estadística
6:
Técnicas de Validación Estadística
Problema 1: De acuerdo con la teoría genética de Mendel, cierta
planta de guisantes debe producir flores blancas, rosas o rojas con
probabilidad 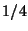 ,
, 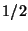 y
y 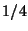 , respectivamente. Para verificar
experimentalmente la teoría, se estudió una muestra de
, respectivamente. Para verificar
experimentalmente la teoría, se estudió una muestra de 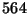 guisantes, donde se encontró que
guisantes, donde se encontró que 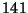 produjeron flores blancas,
produjeron flores blancas,
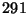 flores rosas y
flores rosas y 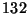 flores rojas.
Aproximar el
flores rojas.
Aproximar el 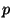 valor de esta muestra:
valor de esta muestra:
a) utilizando un aproximación ji-cuadrada,
b) realizando una simulación.
Problema 2: Calcular una aproximación del 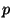 valor de la hipótesis:
``Los siguientes
valor de la hipótesis:
``Los siguientes 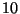 números son aleatorios'':
números son aleatorios'': 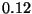 ,
, 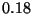 ,
,
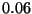 ,
, 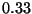 ,
, 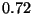 ,
, 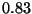 ,
, 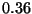 ,
, 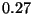 ,
, 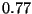 ,
, 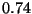 .
.
Problema 3: Calcular una aproximación del 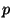 valor de la hipótesis:
``Los siguientes
valor de la hipótesis:
``Los siguientes 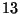 valores provienen de una distribución
exponencial con media
valores provienen de una distribución
exponencial con media 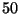 '': 86, 133, 75, 22, 11, 144, 78, 122, 8,
146, 33, 41, 99.
'': 86, 133, 75, 22, 11, 144, 78, 122, 8,
146, 33, 41, 99.
Problema 4: Calcular una aproximación del 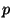 valor de la prueba de
que los siguientes datos corresponden a una distribución binomial
con parámetros
valor de la prueba de
que los siguientes datos corresponden a una distribución binomial
con parámetros 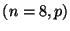 , donde
, donde 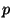 no se conoce:
6, 7, 3, 4, 7, 3, 7, 2, 6, 3, 7, 8, 2, 1, 3, 5, 8, 7.
no se conoce:
6, 7, 3, 4, 7, 3, 7, 2, 6, 3, 7, 8, 2, 1, 3, 5, 8, 7.
Problema 5: Generar los valores correspondientes a 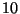 variables
aleatorias exponenciales independientes, cada una con media
variables
aleatorias exponenciales independientes, cada una con media 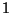 .
Luego, en base al estadístico de prueba de Kolmogorov-Smirnov,
aproxime el
.
Luego, en base al estadístico de prueba de Kolmogorov-Smirnov,
aproxime el 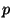 valor de la prueba de que los datos realmente
provienen de una distribución exponencial con media
valor de la prueba de que los datos realmente
provienen de una distribución exponencial con media 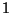 .
.
Problema 6: Un experimento diseñado para comparar dos tratamientos
contra la corrosión arrojó los siguientes datos (los cuales
representan la máxima profundidad de los agujeros en unidades
de milésima de pulgada) en pedazos de alambre sujetos a cada uno
de los tratamientos por separado:
Tratamiento 1: 65.2 67.1 69.4
78.4 74.0 80.3
Tratamiento 2: 59.4 72.1 68.0
66.2 58.5
a) Calcular el 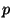 valor exacto de este conjunto de
datos, correspondiente a la hipótesis de que ambos tratamientos
tienen resultados idénticos.
valor exacto de este conjunto de
datos, correspondiente a la hipótesis de que ambos tratamientos
tienen resultados idénticos.
b) Calcular el 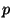 valor aproximado en base a una
aproximación normal,
valor aproximado en base a una
aproximación normal,
c) Calcular el 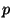 valor aproximado en base a una
simulación.
valor aproximado en base a una
simulación.
Problema 7: Explicar como puede utilizarse la simulación para aproximar
el 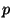 valor en el problema de varias muestras; es decir, cuando se
verifica que un conjunto de
valor en el problema de varias muestras; es decir, cuando se
verifica que un conjunto de 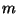 muestras provienen todas de la misma
distribución de probabilidad.
muestras provienen todas de la misma
distribución de probabilidad.
Problema 8: Considerar los siguientes datos resultantes de tres muestras:
Muestra 1: 121 144 158
169 194 211 242
Muestra 2: 099 128 165
193 242 265 302
Muestra 3: 129 134 137
143 152 159 170
Calcular el 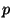 valor aproximado de la prueba: ``Todos
los datos provienen de una única distribución de probabilidad'',
valor aproximado de la prueba: ``Todos
los datos provienen de una única distribución de probabilidad'',
a) utilizando la aproximación ji-cuadrada,
b) utilizando una simulación.
Problema 9: Durante un intervalo de tiempo de longitud 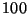 , se han
producido
, se han
producido 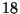 llegadas en los siguientes instantes:
12, 20, 33, 44, 55, 56, 61, 63, 66, 70, 73, 75, 78, 80, 82, 85, 87,
90
llegadas en los siguientes instantes:
12, 20, 33, 44, 55, 56, 61, 63, 66, 70, 73, 75, 78, 80, 82, 85, 87,
90
Aproximar el 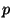 valor de la muestra bajo la hipótesis:
``El proceso de llegada es de Poisson (homogéneo)''.
valor de la muestra bajo la hipótesis:
``El proceso de llegada es de Poisson (homogéneo)''.
Fa.M.A.F ©2001-2002
Pedro Pury
2001-05-28