Objetivo: Calibración del interferómetro
y su empleo en la medición del índice de refracción
del vidrio, del índice de refracción del aire y de la
separación entre las longitudes de onda del doblete del Sodio.
Introducción:
El interferómetro de Michelson es un instrumento de
interferometría por división de amplitud que utiliza
espejos. El divisor del haz consiste en una placa semi-tranparente
![]() (ver Figura 1) que separa la luz incidente en dos
haces perpendiculares de igual amplitud. Los haces son reflejados
sobre sus caminos por los espejos
(ver Figura 1) que separa la luz incidente en dos
haces perpendiculares de igual amplitud. Los haces son reflejados
sobre sus caminos por los espejos ![]() y
y ![]() . El haz reflejado
por
. El haz reflejado
por ![]() es reflejado por el divisor antes del llegar al detector,
donde interfiere con el haz proveniente de
es reflejado por el divisor antes del llegar al detector,
donde interfiere con el haz proveniente de ![]() que atravesó
el divisor.
que atravesó
el divisor.
De esta forma, los haces que llegan al detector por cualquiera
de los caminos resultan reflejados una vez en la placa
semi-transparente, pero el haz que llega desde ![]() atravesó
tres veces el divisor
atravesó
tres veces el divisor ![]() , mientras que el que llega desde
, mientras que el que llega desde ![]() lo atravesó una sola vez. Para igualar el recorrido en vidrio
de los haces, se coloca entonces la placa compensador
lo atravesó una sola vez. Para igualar el recorrido en vidrio
de los haces, se coloca entonces la placa compensador ![]() , que
es una réplica de
, que
es una réplica de ![]() (pero sin el semiplateado), y tambien
posicionada a
(pero sin el semiplateado), y tambien
posicionada a ![]() con respecto a la dirección del haz
horizontal. Considerando la placa compensadora, toda diferencia
de camino óptico entre los haces que arriban al detector proviene
de una diferencia neta de distancia recorrida desde la fuente.
Usualmente se utiliza una fuente extensa que se consigue iluminando
con una lámpara intensa una placa de vidrio esmerilado,
o ensanchando con una lente un haz láser.
Al detector llegan haces paralelos y la imagen del patrón
de interferencia se forma sobre una placa difusora o directamente
proyectando con una lente sobre una pantalla.
con respecto a la dirección del haz
horizontal. Considerando la placa compensadora, toda diferencia
de camino óptico entre los haces que arriban al detector proviene
de una diferencia neta de distancia recorrida desde la fuente.
Usualmente se utiliza una fuente extensa que se consigue iluminando
con una lámpara intensa una placa de vidrio esmerilado,
o ensanchando con una lente un haz láser.
Al detector llegan haces paralelos y la imagen del patrón
de interferencia se forma sobre una placa difusora o directamente
proyectando con una lente sobre una pantalla.
Todos los haces generados por círculos concéntricos
alrededor del eje óptico en la fuente, recorren igual
camino hasta el detector.
Por lo tanto, asumiendo que todos los puntos de la fuente
son coherentes en fase, el patrón de interferencia es de
franjas circulares.
Para entender como estas franjas son generadas en la
Figura 2 se presenta un diagrama conceptual del
interferómetro, donde las imágenes de la fuente ![]() por los espejos
por los espejos ![]() y
y ![]() están representadas por
están representadas por ![]() y
y ![]() , respectivamnete. Del diagrama puede observase que
si
, respectivamnete. Del diagrama puede observase que
si ![]() es la separación efectiva entre los espejos
es la separación efectiva entre los espejos ![]() y
y ![]() ,
la diferencia de camino ópticos de los haces provenientes de un
punto
,
la diferencia de camino ópticos de los haces provenientes de un
punto ![]() , bajo un ángulo de observación
, bajo un ángulo de observación ![]() es
es
![]() .
.
Ahora, teniendo en cuenta que el haz proveviente de ![]() ha sido reflejado externamente por la placa
ha sido reflejado externamente por la placa ![]() , mientras que
el proveniente de
, mientras que
el proveniente de ![]() fue reflejado internamente en
fue reflejado internamente en ![]() ,
ambos haces tiene una diferencia de fase en
,
ambos haces tiene una diferencia de fase en ![]() por reflexión.
Entonces, cuando la diferencia de caminos resulte un número
entero de longitudes de onda se obtendrá interferencia
destructiva
por reflexión.
Entonces, cuando la diferencia de caminos resulte un número
entero de longitudes de onda se obtendrá interferencia
destructiva
Desarrollo Experimental:
En la práctica, la distancia ![]() es inaccesible y sólo puede
contarse el número de franjas que aparecen o desaparecen del
diagrama (por ejemplo del centro del mismo,
es inaccesible y sólo puede
contarse el número de franjas que aparecen o desaparecen del
diagrama (por ejemplo del centro del mismo, ![]() ) para
una variación controlada de la distanca
) para
una variación controlada de la distanca ![]() . Con ese fin uno
de los espejos es móvil a través de un macanismo micrométrico.
. Con ese fin uno
de los espejos es móvil a través de un macanismo micrométrico.
Experiencia 1: Calibración del Tornillo Micrométrico
Se ilumina el instrumento con un haz expandido de una laser de He-Ne.
Se alinean correctamnete todos los elementos del interferómetro
hasta observar nítidamente las franjas circulares.
Se deplaza suavemente el espejo móvil entre dos posiciones
predefinidas del tornillo micrométrico, y se cuenta el número
![]() de franjas que pasan por el diagrama de interferencia.
De la Ec. (1) ó (2) se obtiene
indistintamente (para
de franjas que pasan por el diagrama de interferencia.
De la Ec. (1) ó (2) se obtiene
indistintamente (para ![]() ) que
) que
| (3) |
Experiencia 2: Medición de la separación del doblete de sodio
La luz de una lámpara de Na posee dos líneas de intensidad
y longitudes de onda ![]() y
y ![]() comparables.
La superposición de los diagramas de interferencia de ambas
componentes monocromáticas ocaciona que el diagrama se
destruya cada vez que las franjas brillantes de uno de
los patrones se ubiquen sobre las oscuras del otro. Si esta
condición ocurre cuando se cumplen simultáneamente las
condiciones:
comparables.
La superposición de los diagramas de interferencia de ambas
componentes monocromáticas ocaciona que el diagrama se
destruya cada vez que las franjas brillantes de uno de
los patrones se ubiquen sobre las oscuras del otro. Si esta
condición ocurre cuando se cumplen simultáneamente las
condiciones:
![]() y
y
![]() ,
la condición de destrucción del diagrama volverá
a repetirse para una nueva distancia
,
la condición de destrucción del diagrama volverá
a repetirse para una nueva distancia ![]() tal que:
tal que:
![]() y
y
![]() .
Restando miembro a miembro estas expresiones se obtiene que
.
Restando miembro a miembro estas expresiones se obtiene que
![]() .
Por lo tanto, resulta que la separación entre las longitudes
de onda de las componentes monocromáticas satisface
.
Por lo tanto, resulta que la separación entre las longitudes
de onda de las componentes monocromáticas satisface
| (4) |
Experiencia 3: Medición del índice de refracción del vidrio
Colocando una placa de vidrio plano paralela de espesor ![]() sobre
uno de los haces del interferómetro, puede variarse la diferencia
de camino óptico entre los haces, cambiando el ángulo de
incidencia sobre la placa. Computando la longitud de recorrido en
el interior de la placa, el índice de refracción de la placa
quedará expresado por el número de franjas
sobre
uno de los haces del interferómetro, puede variarse la diferencia
de camino óptico entre los haces, cambiando el ángulo de
incidencia sobre la placa. Computando la longitud de recorrido en
el interior de la placa, el índice de refracción de la placa
quedará expresado por el número de franjas ![]() que cambian en
el patrón de interencia al variar el ángulo de incidencia entre
que cambian en
el patrón de interencia al variar el ángulo de incidencia entre
![]() y
y ![]() , según la expresión
, según la expresión
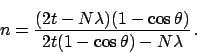 |
(5) |
Experiencia 4: Medición del índice de refracción del aire
Colocando una celda de vacío de longitud ![]() y caras paralelas,
delgadas y transparentes con eje sobre uno de los haces del
interferómetro, pueden cambiarse la longitud de camino, cambiando
la presión del aire encerrado en la celda.
En particular, dado que la frecuencia de la radiación viene dada
por la fuente, la longitud de onda se relaciona con el índice
de refracción del medio según
y caras paralelas,
delgadas y transparentes con eje sobre uno de los haces del
interferómetro, pueden cambiarse la longitud de camino, cambiando
la presión del aire encerrado en la celda.
En particular, dado que la frecuencia de la radiación viene dada
por la fuente, la longitud de onda se relaciona con el índice
de refracción del medio según
![]() , donde
, donde
![]() es la longitud de onda correspondiente al vacío.
es la longitud de onda correspondiente al vacío.
Supongamos que a una presión inicial ![]() , el trayecto del
haz dentro de la celda es un número entero de longitudes de onda
, el trayecto del
haz dentro de la celda es un número entero de longitudes de onda
![]() (tener en cuenta que la celda es atravesada
dos veces). Al cambiar la presión en la celda hasta un valor
final
(tener en cuenta que la celda es atravesada
dos veces). Al cambiar la presión en la celda hasta un valor
final ![]() , el número de longitudes de onda será ahora
, el número de longitudes de onda será ahora
![]() . Así, el número
. Así, el número ![]() de franjas
contadas en el patrón de interferencia será
de franjas
contadas en el patrón de interferencia será
![]() ,
donde se asume que la presión final es mayor que la inicial.
Por lo tanto,
,
donde se asume que la presión final es mayor que la inicial.
Por lo tanto,
![]() .
Suponiendo que la relación
.
Suponiendo que la relación ![]() es lineal
es lineal
![]() ,
resulta que la pendiente está dada por
,
resulta que la pendiente está dada por
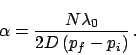 |
(6) |
Bibliografía:
E. Hecht, Optics, Addison Wesley, Reading, MA (1998), 3ed.
F. A. Jenkins y H. E. White, Fundamentos de Óptica, Aguilar, Madrid (1964).