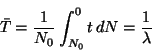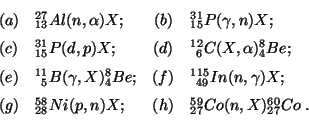Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Física Moderna II
Guía N 3: Procesos Nucleares
3: Procesos Nucleares
Problema 1: La vida media del 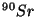 es de 28
años. Determinar:
es de 28
años. Determinar:
a) La constante de desintegración del 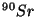 ,
,
b) La actividad de 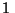 mg de
mg de 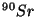 en curies y en
núcleos por segundo,
en curies y en
núcleos por segundo,
c) El tiempo necesario para que 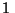 mg se reduzca a
mg se reduzca a
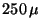 g, y
g, y
d) La actividad al tiempo calculado en c).
Problema 2: Una muestra de material radioactivo
recién preparada se desintegra en un nucleido estable y se mide su
actividad cada 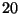 s. Se han medido las siguientes actividades (en
s. Se han medido las siguientes actividades (en
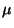 Ci) comenzando en
Ci) comenzando en 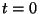 s: 410, 190, 90, 43, 20, 9.6, 4.5,
2.15, 1.00, 0.48, 0.23.
s: 410, 190, 90, 43, 20, 9.6, 4.5,
2.15, 1.00, 0.48, 0.23.
a) Hacer un gráfico del logaritmo natural de la actividad en
función del tiempo.
b) Hallar la constante de desintegración y la vida media de
la muestra.
c) ¿Cuántos núcleos radiactivos había en la muestra
al instante 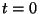 s?.
s?.
Problema 3: Probar que la vida media, 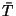 de una
sustancia radioactiva está dada por:
de una
sustancia radioactiva está dada por:
Problema 4: En un reactor nuclear se produce un
nucleido radiactivo a razón de 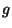 núcleos por segundo.
Calcular el número de núcleos del nucleido radiactivo producidos
en función del tiempo, suponiendo que inicialmente hay
núcleos por segundo.
Calcular el número de núcleos del nucleido radiactivo producidos
en función del tiempo, suponiendo que inicialmente hay 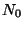 núcleos de la sustancia radiactiva. Considerar los casos en que
núcleos de la sustancia radiactiva. Considerar los casos en que
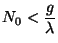 y
y
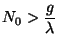 .
.
Problema 5: Suponga que en la cadena radioactiva
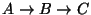 los núcleos de la sustancia
los núcleos de la sustancia 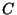 son
estables:
son
estables:
a) Probar que el número de núcleos 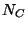 en función
del tiempo es:
en función
del tiempo es:
donde 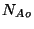 es número inicial de núcleos
es número inicial de núcleos 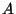 y se supone que
la cantidad inicial de núcleos
y se supone que
la cantidad inicial de núcleos 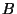 y
y 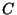 es cero.
es cero.
b) Mostrar 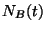 es máximo en el instante:
es máximo en el instante:
Problema 6: Calcular la energía de la
partícula 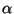 liberada cuando el
liberada cuando el 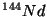 se desintegra
en
se desintegra
en 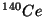 . Calcular además la energía de retroceso del
núcleo residual. Las masas de reposo son
. Calcular además la energía de retroceso del
núcleo residual. Las masas de reposo son 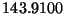 uma y
uma y
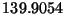 uma respectivamente.
uma respectivamente.
Problema 7: El espectro de desintegración 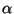 del
del 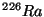 tiene una estructura triple, siendo las energías
de las partículas
tiene una estructura triple, siendo las energías
de las partículas 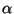 :
: 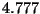 ,
, 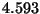 y
y 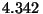 MeV.
Suponiendo que el nucleido residual
MeV.
Suponiendo que el nucleido residual 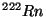 se produzca en el
estado fundamental y 2 estados excitados, dibujar el diagrama de
niveles de energía y mostrar la emisión de rayos
se produzca en el
estado fundamental y 2 estados excitados, dibujar el diagrama de
niveles de energía y mostrar la emisión de rayos 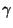 asociados con la transición.
asociados con la transición.
Problema 8: Mostrar los modos posibles de
desintegración del 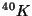 , que tiene una masa en reposo de 39.964
uma. Calcular la energía disponible para cada proceso posible.
, que tiene una masa en reposo de 39.964
uma. Calcular la energía disponible para cada proceso posible.
Problema 9: Probar que el 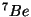 se desintegra por
captura electrónica. Su masa de reposo es
se desintegra por
captura electrónica. Su masa de reposo es 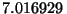 uma.
Calcular la energía y el momentum del neutrino y del núcleo
residual de
uma.
Calcular la energía y el momentum del neutrino y del núcleo
residual de 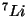 .
.
Problema 10: Completar las siguientes ecuaciones de
reacciones nucleares, colocando en lugar de 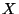 el nucleido o la
patícula correctos:
el nucleido o la
patícula correctos:
Problema 11: La actividad del carbono encontrado en
especímenes vivientes en la actualidad es de 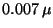 Ci por
kilogramo, debido a la presencia de
Ci por
kilogramo, debido a la presencia de 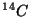 . El carbón proveniente
de los restos arqueológicos de un fogón encontrado en un
campamento indio tienen una actividad de
. El carbón proveniente
de los restos arqueológicos de un fogón encontrado en un
campamento indio tienen una actividad de 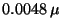 Ci/Kg. La vida
media del
Ci/Kg. La vida
media del 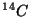 es de 5760 años. Calcule el año en que este
fogón fué utilizado por última vez. Especifíque todas las
suposiciones utilizadas en su cálculo.
es de 5760 años. Calcule el año en que este
fogón fué utilizado por última vez. Especifíque todas las
suposiciones utilizadas en su cálculo.
Problema 12: Cuando el 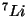 se bombardea con
protones de
se bombardea con
protones de 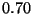 MeV, se producen dos partículas
MeV, se producen dos partículas 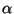 ,
ambas con energía de
,
ambas con energía de 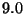 MeV.
MeV.
a) Calcular la energía liberada, 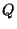 , en la reacción;
, en la reacción;
b) Calcular la diferencia entre la energía cinética
total de las partículas 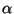 y la energía cinética
inicial del protón en el sistema de laboratorio.
y la energía cinética
inicial del protón en el sistema de laboratorio.
Problema 13: Una lámina de acero borado de las que
se usan en los reactores nucleares como barras de control, tiene
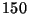 mm de espesor y
mm de espesor y 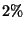 de su peso en boro. Las secciones
eficaces del Fe y B para neutrones rápidos son
de su peso en boro. Las secciones
eficaces del Fe y B para neutrones rápidos son 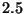 b y
b y 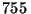 b
respectivamente.
b
respectivamente.
a) Calcular las secciones eficaces macroscópicas de
absorción de cada uno de estos elementos en la lámina de acero
borado.
b) ¿Qué fracción de un haz de neutrones se absorbe al
atravesar esta lámina?.
c) Calcular la sección eficaz macroscópica de la lámina
si el contenido de boro aumenta al 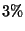 .
.
Densidades:
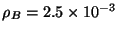 kg/cm
kg/cm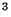 ;
;
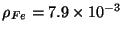 kg/cm
kg/cm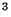 .
.
NOTA: Los siguientes tres problemas ilustran
los razonamientos que condujeron a Chadwick en 1932 al descubrimiento
del neutrón.
Problema 14: Cuando las partículas 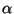 de
de
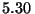 MeV proveniente de una fuente de
MeV proveniente de una fuente de
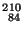 Po
incidían sobre un blanco de
Po
incidían sobre un blanco de 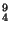 Be se encuentraba una
radiación desconocida sin carga. Suponiendo que la radiación
emergente corresponde a rayos
Be se encuentraba una
radiación desconocida sin carga. Suponiendo que la radiación
emergente corresponde a rayos 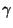 , calcular la energía de
los rayos
, calcular la energía de
los rayos 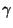 que emergen del banco de
que emergen del banco de 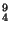 Be en la
dirección de incidencia.
Be en la
dirección de incidencia.
Problema 15: En experimentos separados, la radiación
desconocida del problema anterior se hizo incidir sobre un blanco de
parafina rico en protones y sobre un blanco de 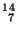 N.
Suponiendo aún que esta radiación corresponde a fotones,
determinar la mínima energía del fotón para producir en
cada experimento protones en retroceso con
N.
Suponiendo aún que esta radiación corresponde a fotones,
determinar la mínima energía del fotón para producir en
cada experimento protones en retroceso con 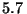 MeV y núcleos de
MeV y núcleos de
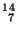 N en retroceso con
N en retroceso con 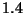 MeV.
Compare estas energías con el resultado del problema anterior.
MeV.
Compare estas energías con el resultado del problema anterior.
Problema 16: Suponiendo en el problema anterior que
los protones y núcleos de 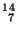 N en retroceso fueron el
resultado de una colisión frontal con una partícula incidente
masiva, encontrar la correspondiente masa y energía cinética
inicial.
N en retroceso fueron el
resultado de una colisión frontal con una partícula incidente
masiva, encontrar la correspondiente masa y energía cinética
inicial.
Fa.M.A.F ©1995
Pedro Pury
2001-02-13